基于计时器的最小连通支配集生成算法
杨阳,芮兰兰,郭少勇,邱雪松,亓峰
(北京邮电大学 网络与交换技术国家重点实验室,北京 100876)
1 引言
移动自组织网络(MANET)旨在建立一种无需固定设施便可即时组网、随时通信的数据网络。这要求设计的路由算法必须具备收敛快、自适应、高效能等特性。洪泛路由模式虽然简单,但会导致网络数据的高冗余,甚至广播风暴[1]。基于最小连通支配集(MCDS, minimum connected dominating set)的分层路由模式将路由过程简化到 MCDS生成的较小子网,构成高一级的虚拟骨干网,负责路由计算和维护,大幅提高路由效率。然而,MANET拓扑结构的频繁变动使虚拟骨干网逐步分崩离析,导致路由过程发生拥塞甚至不可达,严重影响通信质量。因此,有效的MCDS算法必须随时适应拓扑变化,快速构建和恢复虚拟骨干网,增强路由顽健性。
MCDS属于NP-C问题[2],因此在实际应用中常使用近似算法,包括集中式算法和分布式算法。集中式算法需要全局拓扑信息,虽能生成较小的连通支配集(CDS),但不适合多数无线应用,如Greedy算法[3];分布式算法通过节点信息交换、协商等机制构造CDS,符合MANET的自组织特性。Dai等人提出了基于剪枝的Rule k算法[4],Vahid等人扩展出高效的Pruning算法[5],Rajiv等人提出了基于协作覆盖的算法[6]。文献[7~16]通过图论建立数学模型,应用聚簇、斯特纳树、独立集、弱连通支配集、最小权值连通支配集等概念,研究MANET的连通性问题。现有研究成果主要根据特定需求生成CDS,大多忽视MANET拓扑的动态性,对如何维持虚拟骨干网讨论较少,限制了算法适用范围。
本文针对节点频繁移动的大规模 MANET环境,提出了基于计时器的 CDS生成算法(TB-CDS,timer based-CDS),利用节点计时器的超时机制控制信息交换、环境感知,并运用启发式分簇策略进行网络逻辑分区,实现动态拓扑下虚拟骨干网的并行构建与重构,具有较广泛的普遍通用性。
2 TB-CDS算法
2.1 问题描述和相关定义
假设MANET有n个无线节点,每个节点有唯一的标识ID,信号覆盖半径为r,在此距离内无线节点间是连通的。为优化网络的资源分配和路由效率,考虑如何利用节点计时器更新环境信息,使这n个节点通过协商,陆续加入不同区域,分布式地选取若干节点组成虚拟骨干网,并根据不同拓扑变化调整骨干网,维持其连通性。
定义1 图的相关定义
无向图 G=(V,E,d)为单位圆图,其中,V和 E分别代表顶点集和边集。记N(u)={v|(u, v)∈E}为节点u的邻居集;d表示以V中顶点为圆心的圆的半径,若边(u, v)∈E,则顶点u, v间的距离|u−v|≤d。以下将无向图G=(V,E,d)简称为图G=(V,E)。
定义2 最小连通支配集
图G=(V,E),CV⊆,若∀u∈V−C,都∃v∈C,(u,v)∈E,则称v为支配节点,C为G的支配集。若由支配集C导出的子图是连通图,称C为连通支配集(CDS),节点最少的连通支配集称为最小连通支配集(MCDS),CDS中的节点组成虚拟骨干网。
定义3 节点的属性定义
任意节点v的标识ID记为nid(v);簇(区域)号:aid(v);度为δ(v);角色为role(v)=Enum{newcomer,dominatee, dominator}。节点 v没有加入区域⇔role(v) =newcomer(新节点)。节点v已加入区域但不属于支配集⇔role(v)= dominatee(被支配节点)。节点v已加入区域且属于支配集⇔role(v)= dominator (支配节点)。节点v是初始簇头(区域发起者)⇔role(v) =dominator,aid(v)= nid(v)。
定义4 节点的基本信息定义
任意节点v的基本信息记为Info(v)={nid(v), aid(v),role(v), δ(v)}。若 role(v)≠ newcomer,则它的异簇邻居集记为 S(v)={u| u∈N(v)∧ aid(u)≠ aid(v)∧ role(u)≠ newcomer},异簇邻居信息集记为SN(v)= {Info(u)|u∈ S(v)}。
定义5 节点的消息定义
节点发送 4 种消息:Status,JoinArea,AllyArea,BeaconArea。其中,Status(Info(v),SN(v)(可选)),用于节点 v周期性广播自身状态;JoinArea(Info(u),Info(v))用于节点u声明以节点v为接入点加入v所在区域;AllyArea(Info(u),Info(v))用于节点u申请与异簇节点 v连通所属区域的骨干网;Beacon Area(Info(v), t),用于初始簇头v周期性广播区域生存消息,其中,t为节点v发送消息的时间戳,它由该区域内的dominator节点多跳转发。
定义6 节点的计时器定义
节点使用2种计时器:SendTimer、RecvTimer。分别控制消息发送和接收,都能引发超时事件。如节点u启动SendTimer(Status),将周期性广播Status(Info(u));启动 RecvTimer(Status(Info(v))),监控邻居v的生存。
2.2 算法步骤
TB-CDS算法分为三阶段:阶段一,在计时器控制下,邻居节点交换信息,利用启发式方法选举初始簇头,声明各自区域;阶段二,节点选择接入节点,陆续加入不同区域,分布式地构建以初始簇头为根节点的域内 CDS生成树;阶段三,通过调整边界节点连通相邻区域的 CDS生成树,完成虚拟骨干网的构建。计时器的超时机制使节点能够感知拓扑环境变化,实现虚拟骨干网的拓扑重构。假设的MANET由图G=(V,E)表示。
阶段Ⅰ 基于启发式策略的分区
1) 所有节点 u∈V 设置 role(u)←newcomer,aid(u)←nid(u),δ(u)←0,完成初始化;
2) 所有节点 u∈V开启计时器 SendTimer(Status),周期性广播Status(Info(u)),进行邻居发现;
3) 节点间接收邻居Status,更新自身Info,存储邻居 Info。若首次发现邻居 v,则启动 RecvTimer(Status(Info(v))),否则予以重置;
4) 2次Status广播后,每个节点u∈V能够获取1跳内邻居的最新Info;
5) 每个newcomer节点u∈V,若N(u)≠∅,则进行初始簇头选举。选举的优先级序列设为P(v)=(role(v),δ(v),nid(v)),并规定 P(v)>P(u) (v≠ u),当且仅当满足下列任意条件时成立

计算 MaxP(u)=Max({ P(v)| v∈N(u) });若P(u)>Max−P(u),则继续 6);若 P(u)<MaxP(u)=P(v),其中,role(v)=newcomer,则转到 7),role(v)=dominator或dominatee,则转到8);
6) 此newcomer节点u自选举为初始簇头,设置 role(u)←dominator,开启 SendTimer(Beacon Area),周期性广播 BeaconArea(Info(u),t0),区域号设为aid(u);继续7);
在阶段Ⅰ中,由于节点标识符nid的唯一性,不同节点的优先级序列P必不等,因此一定能选举出若干初始簇头。节点的role越大、δ越大,覆盖节点越多,选举优先级P就越高,有利于缩小CDS。
阶段Ⅱ 区域CDS的生成
7) 每个newcomer节点u∈V,继续接收Status,更新邻居的Info;转到5);
8) 若 newcomer节点 u∈V计算得 P(u)<MaxP(u)=P(v),role(v)= dominatee或 dominator,设置 aid(u)←aid(v),role(u)←dominatee。向节点 v发送 Join-Area(Info(u),Info(v)),表明已加入v所属区域aid(v),并启动RecvTimer(BeaconArea),监测区域存活;
9) 若 dominator节点 v∈V收到 JoinArea(Info(u),Info(v)),顺带更新Info(u);若为dominatee节点v,则设置role(v)←dominator,顺带更新Info(u);
10) 每个dominator节点u∈V都维护一个时间戳 T来判断 BeaconArea(Info(v),t0)消息是否过时。若T<t0,则广播转发,设置T←t0,重置RecvTimer(BeaconArea);继续 11)。
每个newcomer节点总能在有限时间内,自选举为初始簇头dominator,或选择邻居dominatee、dominator节点作为接入点(父节点)加入区域。每个初始簇头都以自身为根节点构建 CDS生成树,吸纳newcomer节点加入区域。其中,dominator节点为枝干节点(虚拟骨干网),dominatee节点为叶子节点,伴随树的“生长”,覆盖的节点逐渐增多,区域范围不断扩大。
阶段Ⅲ 区域边界的调整
11) 每个dominatee或dominator节点u∈V,若处于区域边界,则广播 Status(Info(u),SN(u))。因此可获得2跳内的异簇节点信息,用于计算是否连通相邻区域。设节点(v,w)代表连通区域A与B的边界网关组合,MaxR(A,B)=Max({R(v,w)|aid(v)=A∧aid(w)=B∧(v,w)∈E})代表优先级最高的组合;网关组合的优先级序列为R(v,w)=(role(v), role(w), nid(v),nid(w)),其中,v∈S(w)且aid(v)<aid(w),并规定R(v,w)>R(x,y),当且仅当满足下列任意条件时成立

若节点u计算得MaxR(aid(u), aid(v))=R(u,v),则继续12),否则周期性计算MaxR;
12) 此节点 u向节点 v发送 AllyArea(Info(u),Info(v)),申请连通节点v所在区域的CDS;节点v收到此消息后回复AllyArea(Info(v),Info(u)),表明同意连通。双方收到对方发送的AllyArea后,若role= dominatee,则设置 role←dominator。
根据优先级序列R的定义,aid较小的节点总是首先发送AllyArea;2个dominator节点的组合将优先成为边界网关节点。最后,当所有节点的role不再改变时,算法达到收敛,网络趋于稳定,所有区域的CDS连通成全局CDS,构成虚拟骨干网。
上述算法及步骤对应的伪码如图1和图2所示。

图1 伪码1任意节点u的状态处理线程

图2 伪码2任意节点u的消息处理线程
阶段Ⅰ Ⅱ Ⅲ中的计时器超时处理
a) 若节点u∈V的RecvTimer(Status(Info(v)))超时,则删除邻居节点 v的信息,更新 N(u)后,若N(u)=∅,则删除所有计时器,转到1)后重新初始化为newcomer节点;
b) 若节点 u∈V的 RecvTimer(BeaconArea(Info(v),T))超时,则认为已脱离初始簇头v的管辖,删除所有计时器,转到2)后重新初始化为new- comer节点;
c) 若节点 u∈V的 SendTimer(Status)超时,则广播Status消息并重置该计时器;
d) 若初始簇头 u∈V的 SendTimer(Beacon-Area)超时,则广播 BeaconArea消息并重置该计时器;
拓扑变化可归结为节点撤出和加入或2种动作的组合。节点撤出发生于故障、电池耗尽、退出网络时,引发邻居节点 RecvTimer (Status)超时,若dominator节点撤出,可能引发某些节点RecvTimer(BeaconArea)超时;节点加入发生于加入网络、故障恢复时,将引发邻居节点启动RecvTimer(Status)。图3为节点角色的转换示意,每个节点在不同阶段,根据拓扑变化、消息交互作出对应的角色转换。TB-CDS算法依赖计时器控制节点进行环境感知、角色转换,实现虚拟骨干网的自适应生成及重构。
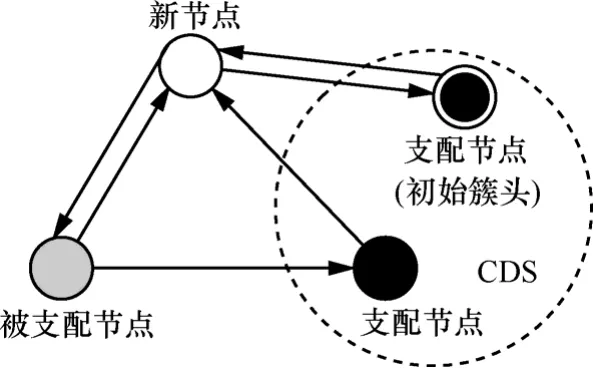
图3 节点的角色转换
2.3 算法应用举例
图4~图6描绘了TB-CDS的执行过程。
图 4(a)展示算法的阶段Ⅰ,通过计算 MaxP,节点1、节点2、节点3自选举为初始簇头。图4(b)表明阶段Ⅱ的开始,向节点1发出JoinArea后,节点 4、节点 13、节点 17、节点 18、节点 20成为dominatee,加入区域A1;节点6、节点9、节点11、节点16、节点19加入A2;节点5、节点8、节点14、节点15、节点21加入A3。此时节点22、节点 23加入网络,如图 4(c)所示。由于 P(v17)=(dominatee,3,17)>P(v20)=(dominatee,3,20),节点 22向节点17发送JoinArea后加入A1。图5(a)展示了阶段Ⅲ的开始,边界节点5、节点7、节点12、节点15计算MaxR(A1,A3),获知边界网关仅有2种组合R(v7,v15)>R(v12,v5)。因此节点7、节点15互相发送AllyArea后成为dominator。同理,边界节点9、节点8、节点10、节点13成为dominator,分别连通A2与A3、A2与A1,如图5(b),已生成CDS,所有dominator节点构成虚拟骨干网。

图4 区域构建
此时,节点9由A2移至A1,无法接收A2内的BeaconArea消息,导致RecvTimer(BeaconArea)超时,重新初始化为newcomer。经过邻居发现,节点9选择节点4作为接入节点加入A1,节点4成为dominator。节点2、节点8、节点11、节点19的RecvTimer(Status (Info(v9)))超时,将删除节点9的Info;节点11计算MaxR(A2,A3)得知R(v11,v8)的优先级最高,向节点8发送AllyArea并收到回复后,成为dominator重新连通A2和A3,如图5(c)所示。
如图6(a)所示,当节点7、节点8故障后,节点12,5成为dominator,重新连通A1与A3,因为此时的 MaxR(A1,A3)=R(v12,v5)。图 6(b)中,A3的初始簇头节点3发生故障,导致节点5、节点14、节点15、节点21的RecvTimer (BeaconArea)超时,全都初始化为 newcomer。调整后的稳定拓扑如图6(c)所示,节点14选举为新的初始簇头,虚拟骨干网完成重构。
2.4 算法正确性证明
定理 1 若初始网络是连通的,当所有节点的role不再改变,区域边界通过 dominator节点连通时,网络拓扑达到稳定状态。
证明 初始时,每个节点都是newcomer,经过2轮Status广播,能获取邻居的最新Info,经过计算选举优先级MaxP,必然有m个节点能成为初始簇头,m>0。设当前时刻为t,节点变更role和连通区域等操作所需的时间上限为 T,总节点数为 n(n>m),剩余newcomer节点数量为n−m,那么在至多t+(n−m)T时刻,这些节点将全部加入到m个区域中。在t+(n−m)T+T时刻前,区域边界必能连通,网络拓扑达到稳定状态。
ATT7022B采用QFP44封装,内部集成了多个适于电信号采集、变换,能对电能、电功率、电流有效值、电压有效值、功率因数、频率等参数进行精确计算。采样信号由电流信道和电压信道进入,经过AD转换之后送到数字信号处理模块中,数字信号处理模块对采集来的数据进行运算处理之后,可以得到全波、基波和谐波的有功、无功、视在功率,有功、无功能量,电流、电压有效值,频率、功率因数、相角等参数[2-3]。
引理 1 若初始网络是连通的,则稳定状态下不存在newcomer节点。

图5 虚拟骨干网的生成

图6 虚拟骨干网的重构
证明(反证法) 假设在稳定状态下存在newcomer节点,不妨设为u,由于初始网络是连通的,那么u拥有至少一个邻居节点v。经过有限时间,节点u将加入某个区域或自选举为初始簇头,role(u)将至少改变一次,与定理1矛盾,得证。
引理 2 每个 dominatee节点至少与一个dominator节点相邻。
证明 区域 CDS生成树构造过程中,newcomer节点总是选择优先级最高的邻居节点作为接入节点(父节点),成为dominatee,该邻居节点则成为dominator。因此,newcomer节点成为dominatee节点后,至少与一个dominator节点相邻。
引理 3 若初始网络是连通的,则稳定状态下所有dominator节点构成图G引导的连通子图。
证明 每个区域的 dominator节点为该区域内CDS生成树的枝干节点,构成图 G引导的连通子图。由定理 1,在稳定状态下,区域边界通过dominator节点连通,因此,所有dominator节点能构成图G引导的连通子图。
定理 2 若初始网络是连通的,则稳定状态下所有dominator节点构成CDS,即虚拟骨干网。
2.5 算法性能分析
本节将在最差情况下,分析TB-CDS算法的时间复杂度和消息复杂度。
假设节点做出任何决策所需的时间上限为常数T,节点广播Status的周期为Ts, Ts<T,初始簇头广播BeaconArea的周期为TB, TB<T。如图7所示,当所有节点分布于一条直接上,并以nid升序或降序排列时,算法性能最差。节点2成为初始簇头。初始簇头选举所需的时间上限为T,剩余n−1个节点加入区域所需的时间上限为(n−2)T,因此,构建CDS所需时间上限为(n−1)T,算法时间复杂度为O(n)。设发送的 Status数为 Ms,BeaconArea数为MB,JoinArea数为MJ。n个节点在(n−1)T内广播的Status数量为
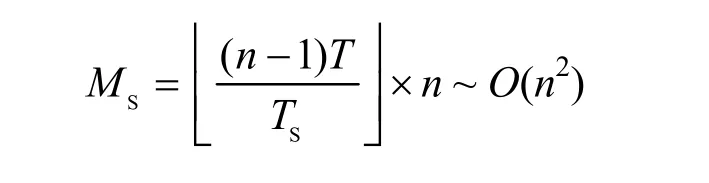
JoinArea数量为 MJ=n−1~O(n)。BeaconArea由dominator节点中继广播,在构建CDS的过程中,dominator节点的数量逐步增至n−2个,则

(n−2 个 dominator 节点在(n−1)×T 时间内发送Beacon Area的数量)。因此,构建CDS所需发送消息总数为 M=Ms+MB+MJ~O(n2)。

图7 最差情况下的拓扑结构
最差情况下,TB-CDS算法的时间复杂度为O(n),消息复杂度为O(n2)。事实上,TB-CDS算法的收敛时间取决于并行构建区域的时间开销,因此一般情况下的时间复杂度为O(D),其中,D为最大区域的直径,D通常比n小得多;以下将通过仿真实验得出,一般情况下的消息复杂度为O(nlogn)。
3 仿真实验
本文采用OPNET软件,模拟拥有n个节点的MANET网络(n取值为40~1000),随机部署于100m×100m的矩形监测区域。节点传输功率设置为3.65 E-6 W和9.25E-7 W,对应的通信半径r分别约为15m和30m;数据分组大小设置为512byte,分组发送率为1packet/s。实验针对每种算法,根据n、r的取值产生300次随机拓扑结构,统计性能指标(CDS大小、消息开销、拓扑调整轮数),取均值作为仿真结果。TB-CDS算法中Status的发送周期Ts和超时期限 Es分别设置为 1000ms、5000ms;BeaconArea的发送周期TB和超时期限EB分别设置为3000ms、9000ms。
本文选取经典的Greedy算法[3]和Rule k算法[4],以及 Pruning算法[5]用于在静态拓扑下与 TB-CDS算法比较收敛时的CDS大小、消息开销这2项基本指标。这 3种算法生成的 CDS大小较为趋近MCDS的近似解,适合多数算法衡量此项指标。
如图8(a)、图8(b)所示,当r=15m,n∈[40,200]时,TB-CDS算法生成的CDS大于Greedy算法的,但远小于另2种算法,而n∈[200,1000]时,TB-CDS算法逐渐接近Pruning算法,因为区域数量的增加导致边界网关增多。由图8(c)、图8(d)可知,r=30m时,邻居大量增加使得CDS减小。在n∈[40,200],Pruning算法比TB-CDS算法稍差,但在n∈[200,1000]稍优,因为Pruning算法中每个节点拥有更多邻居信息,删除的冗余节点也更多,实验表明,一般情况下TB-CDS算法生成的CDS的大小具备竞争力,在节点稠密的环境下更为优异。

图8 不同节点数下生成CDS的大小
Greedy算法基于已知拓扑结构,节点间无需消息交换;Rule k算法与Pruning算法的消息开销相近,因此只选取TB-CDS算法与Pruning算法比较消息复杂度。如图9(a),2种r下的TB-CDS算法消息数量接近,小于 Pruning算法;在图 9(b)中,Pruning消息数量远高于TB-CDS算法,因为所有节点需要获取两跳内所有邻居的节点信息,消息开销受r影响很大。TB-CDS算法中r的增加使区域数量、支配节点数减少,降低了维持区域的消息开销。实验表明,一般情况下TB-CDS算法的消息复杂度为O(nlogn)。
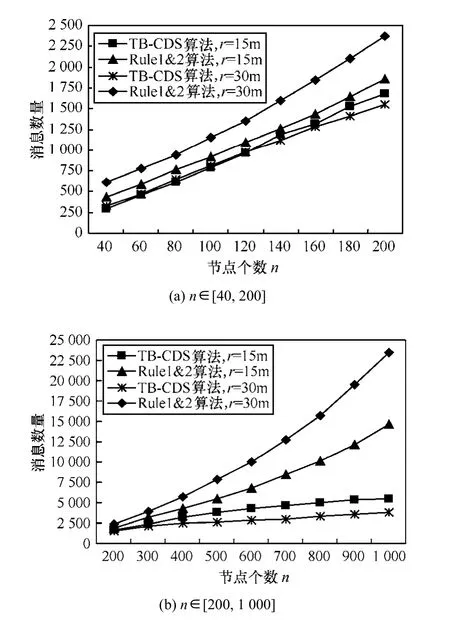
图9 收敛时已发送的消息数量
考察TB-CDS算法在大型网络下对拓扑变化的适应速度。当算法达到收敛时,计算5%,10%的节点撤出网络、加入网络、随机移动(分别用W, J, M表示)后虚拟骨干网完成重构需要几轮节点调整操作(接收消息,更新拓扑信息,优先级P, R计算,发送消息,更改角色)。如图10所示,同等节点数量下,r越大则邻居节点越多,调整轮数较小。节点撤出网络和发生移动将影响虚拟骨干网的连通性,相关节点的计时器超时后,才开始重构骨干网,而新节点的加入对连通性没有影响,只需添加骨干网节点即可恢复,因此调整轮数大大减少。

图10 拓扑发生变化后,算法所需调整轮数
4 结束语
本文针对MANET节点移动较为频繁的特点,提出基于计时器思想的MCDS生成(TB-CDS)算法,分布式地构建虚拟骨干网,解决了维持骨干网连通性的关键问题,实现了动态拓扑下骨干网的快速重构,证明了算法的正确性。仿真结果表明,TB-CDS算法能以较低的开销生成较小的虚拟骨干网,不但有效减少了冗余转发节点,而且具有良好的自愈能力。由于TB-CDS算法的仿真实验环境较为理想,尚缺乏针对终端节点间差异性的考虑。因此下一步将综合终端差异性来完善TB-CDS算法,并应用于MANET路由协议,以期作为分层按需路由的基础。
[1]唐勇, 周明天, 张欣.无线传感器网络路由协议研究进展[J].软件学报,2006,17(3):410-421.TANG Y, ZHOU M T, ZHANG X.Overview of routing protocols in wireless sensor networks[J].Journal of Software, 2006, 17(3):410-421.
[2]GAREY M R, JOHNSON D S.Computers and Intractability:A Guide to the Theory of NP-Completeness[M].New York:W H Freeman &Co, 1979.
[3]DAS B, BHARGHAVAN V.Routing in ad-hoc networks using minimum connected dominating sets[A].Proceedings of the IEEE International Conference on Communications[C].Montreal, Canada, 1997.376-380.
[4]DAI F, WU J.An extended localized algorithm for connected dominating set formation in ad hoc wireless networks[J].IEEE Transactions on Parallel and Distributed Systems,2004,15(10):908-920.
[5]VAHID G, SEYED N, MOJTABA M.Connected dominating set construction using an efficient pruning method in ad hoc networks[A].Wireless Internet Conference (IEEE WICON) The 5th Annual ICST[C].Singapore, 2010.1-8.
[6]RAJIV M, CHITTARANJAN M.Minimum connected dominating set using a collaborative cover heuristic for ad hoc sensor networks[J].IEEE Transactions on Parallel and Distributed Systems, 2010, 21(3):292-302.
[7]BO H.Zone-based virtual backbone formation in wireless ad hoc networks[J].Ad Hoc Networks, 2009, 7:183-200.
[8]TORKESTANI J A, MEYBODI M R.An intelligent backbone formation algorithm for wireless ad hoc networks based on distributed learning automata[J].Computer Networks, 2010, 54:826-843.
[9]KIM D Y, ZHANG Z, LI X Y, et al.Better approximation algorithm for computing connected dominating sets in unit ball graphs[J].IEEE Transactions on Mobile Computing, 2010, 9(8):1108-1118.
[10]DING L, GAO X F, WU W L, et al.Distributed construction of connected dominating sets with minimum routing cost in wireless networks[A].Distributed Computing Systems (IEEE ICDCS)[C].Genoa,Italy, 2010.448-457.
[11]WANG Y M, ZHAO D S.A serial MIS based CDS constructing algorithm for wireless networks[A].Green Computing and Communications(GreenCom)IEEE/ACM Int'l Conference on & Int'l Conference on Cyber Physical and Social Computing (CPSCom)[C].Hangzhou,China, 2010, 466-469.
[12]DING L, WU W L, WILLSON J, et al.Efficient algorithms for topology control problem with routing cost constraints in wireless networks[J].IEEE Transactions on Parallel and Distributed Systems,2011, 22(10):1061-1069.
[13]ZHENG C, SUN S X, HUANG T Y.Constructing distributed connected dominating sets in wireless ad hoc and sensor networks[J].Journal of Software, 2011, 22(5):1053-1066.
[14]YINA B, SHI H C, SHANG Y.An efficient algorithm for constructing a connected dominating set in mobile ad hoc networks[J].Journal of Parallel and Distributed Computing, 2011, 77:27-39.
[15]ZOU F, WANG Y X, XU X H, et al.New approximations for mini- mum weighted dominating sets and minimum-weighted connected dominating sets on unit disk graphs[J].Theoretical Computer Science, 2011,412:198-208.
[16]ARIYAM D, CHITTARANJAN M, CHRIS R.An improved greedy construction of CDS in MANET[A].Wireless Communications and Networking Conference (IEEE WCNC)[C].Cancun, Mexico, 2011.790-795.

