2013年福建省数学高考试题带来的启示
●
(永安市第一中学 福建永安 366000)
2013年福建省数学高考试题带来的启示
●宋建华
(永安市第一中学 福建永安 366000)
一年一度的高考如期而至,新鲜出炉的高考试题令人赏心悦目,这些试题凝聚着命题者的心血,完美地诠释了《高考数学考纲》与《高考数学考试说明》的要求,给我们带来颇多的启示.
1 数学探究是福建省数学高考试题的特色
《高中数学课程标准》要求在教学过程中注重数学探究,这是由于数学探究有助于学生了解数学概念和结论产生的过程;有助于培养学生勇于质疑和善于反思的习惯,培养学生发现、提出、解决数学问题的能力;有助于发展学生的创新意识和实践能力.
在高考试题中出现的数学探究主要考查学生围绕某个数学问题,观察、分析数学事实,提出有意义的数学问题,或者猜测、探求适当的数学结论、规律,给出解释或证明的能力,数学探究已成为检测学生学习潜能的一种重要的手段.
福建省的数学高考试卷特别钟情于数学探究并且逐渐形成特色,从近5年的试卷中可以得到验证.表1为福建省实施课标课程的5年来,在理科卷6道解答题中涉及数学探究的试题分布情况,从中可以看出数学探究所占的份量.

表1 近5年福建省理科卷6道解答题中涉及数学探究的试题分布情况
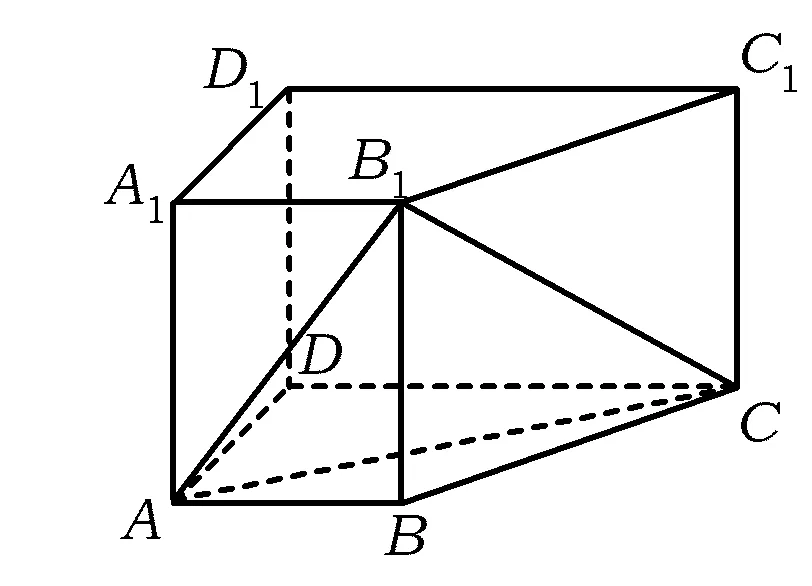
图1
例1如图1,在四棱柱ABCD-A1B1C1D1中,侧棱AA1⊥底面ABCD,AB∥DC,AA1=1,AB=3k,AD=4k,BC=5k,DC=6k(k>0).
(1),(2)(略)
(3)现将与四棱柱ABCD-A1B1C1D1形状和大小完全相同的2个四棱柱拼成一个新的四棱柱,规定:若拼成的新四棱柱形状和大小完全相同,则视为同一种拼接方案,问共有几种不同的拼接方案?在这些拼接成的新四棱柱中,记其中最小的表面积为f(k),写出f(k)的解析式(直接写出答案,不必说明理由).
(2013年福建省数学高考理科试题第19题)
分析进行数学探究的试题从结构看有:条件开放的探究、结论开放的探究以及条件与结论均开放的探究;从试题的类型看有:方案设计型的探究、规律探索型的探究、解题策略型的探究等.本题第(3)小题要求对已知几何体进行拼接从而构造出新的几何体,问题的开放性设计利于学生多角度地进行探究,考查了学生的空间想象能力和思维的严谨性、发散性,而直接写出答案不必说明理由的要求,则能反映学生的直觉思维与抽象概括能力.
2 数学应用意识得到强化
《考纲》与《考试说明》均有要求发展学生的数学应用意识,重视应用意识的考查.对数学应用意识的考查主要采用解决应用问题的形式,依据现实的生活背景,提炼相关的数量关系,将现实问题转化为数学问题,构造数学模型并加以解决.
数学应用意识考查的难点与核心在于数学建模,所谓数学建模就是运用数学思想、方法和知识解决实际问题的过程,是寻求建立数学模型方法的过程.《课程标准》对高中阶段的数学建模也有详细的要求,数学建模有助于学生体验数学在解决实际问题中的价值和作用,体验数学与日常生活和其他学科的联系,体验综合运用知识和方法解决实际问题的过程,增强应用意识.
由于客观条件及学生知识水平的限制,数学高考应用意识的考查还难以与数学建模划等号,实际操作中常常对课本例、习题进行改造,或对常规的试题增加生活背景,或以概率统计的面目出现,这些做法都能达到考查学生数学应用意识的目的.
例2某工厂有25周岁以上(含25周岁)工人300名,25周岁以下工人200名.为研究工人的日平均生产量是否与年龄有关,现采用分层抽样的方法,从中抽取了100名工人,先统计了他们某月的日平均生产件数,然后按工人年龄在“25周岁以上(含25周岁)”和“25周岁以下”分为2组,再将2组工人的日平均生产件数分为5组:[50,60),[60,70),[70,80),[80,90),[90,100)分别加以统计,得到如图2所示的频率分布直方图.

图2
(1)从样本中日平均生产件数不足60件的工人中随机抽取2人,求至少抽到一名“25周岁以下组”工人的概率;
(2)规定日平均生产件数不少于80件者为“生产能手”,请你根据已知条件完成列联表,并判断是否有90%的把握认为“生产能手与工人所在的年龄组有关”?
(2013年福建省数学高考文科试题第19题)
分析我们知道获取数学知识并不是最终目的,应用数学知识去解决生产、生活中的实际问题才是学习数学的出发点和归宿.本题从实际问题出发,考查了学生应用概率统计知识与方法解决实际问题的能力,体现了概率与统计知识在决策中的作用.
3 让绚丽的数学文化之花为数学试卷增色
《课程标准》提出并对数学文化进行了详尽的描述与要求,这是前所未有的,体现了设计者对数学文化的重视.数学不仅是数学知识的汇总,更重要的是它包含着丰富而深刻的文化内涵,通过感悟数学文化,可以让学生更深刻地感受到数学对于人们的影响,激发学生学习数学的热情.
通过数学文化的方式对数学知识进行考查是一种新的形式,当课堂教学中已经相当重视数学文化的渗透与传播之时,在数学高考试题中,如何体现数学文化是一个全新的课题,进行合理地考查将有助于加强学生对数学文化的感悟,有助于加强教师对数学文化的重视与传承.福建省数学高考试卷中对此虽有体现但仍显不足,湖北省的高考试卷在这方面有许多做法值得借鉴.
例3我国古代数学名著《数书九章》中有“天池盆测雨”题:在下雨时,用一个圆台形的天池盆接雨水.天池盆盆口直径为二尺八寸,盆底直径为一尺二寸,盆深一尺八寸.若盆中积水深九寸,则平地降雨量是______寸(注:①平地降雨量等于盆中积水体积除以盆口面积;②一尺等于十寸).
(2013年湖北省数学高考文科试题第16题)
分析《数书九章》是南宋数学家秦九韶唯一的数学著作,书中列有81问,算题共分为9类,该书概括了宋元时期中国传统数学的主要成就,标志着中国古代数学的高峰.本题借助“天池盆测雨”这个问题体现数学文化,从知识的层面看只是考查圆台的体积以及圆的面积,要求不高,但通过这样的考查方式却能让学生感受到中华数学文化灿烂的瑰宝.
4 数学本质是问题之源,是考查之本
《课程标准》指出:高中数学课程应返璞归真,努力揭示数学概念、法则、结论的发展过程和本质;《考纲》也规定高考要考查考生对数学思想方法和数学本质的理解水平.
数学本质在数学发展史上有许多不同的见解,数学本质的内涵应包括:数学知识的内在联系、数学规律的形成过程、数学思想方法的提炼、数学理性精神的体验等.数学本质是问题之源,是考查之本,数学高考试题若能在数学本质上进行设问,多考查数学本质的内涵,则能更好地让学生体会到数学最核心、最本质的内容,体会知识间的联系,改变教师教学中“重结果、轻过程”的现象,加深广大师生对数学本质的理解.
例4已知x与y之间的几组数据如表2:
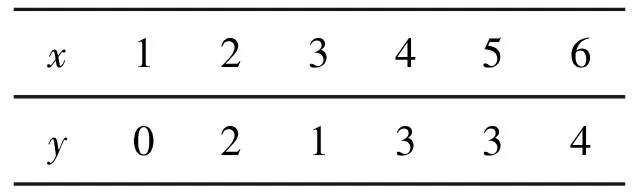
表2 x与y的值
假设根据表2中数据所得线性回归直线方程为y=bx+a,若某同学根据表2中的前2组数据(1,0)和(2,2)求得的直线方程为y′=b′x+a′,则以下结论正确的是
( )
A.b>b′,a>a′ B.b>b′,a (2013年福建省数学高考文科试题第9题) 分析本题有别于以往对线性回归的考查方式,如果套用公式进行计算将非常繁杂且不是命题者的本意.本题将设问放置在线性回归方程中最为本质的知识点(散点图)上进行考查,让学生从数学的本质来体会知识的联系,显得真实而自然、简单而优美,对于线性回归知识形成有序的、相互联系的认知结构很有帮助. 数学高考试卷不仅承载着选拔的功能,也承担着指导教学的任务.如何破除当前教学中存在的“题海战术”等种种弊端,规避固有模式是一种行之有效的策略,它减少了猜题、压题的冲动.规避模式可以采用更灵活的试题编排顺序,或者在数学知识的考查上更多地进行交汇. 现阶段高中数学的主干知识包括函数与导数、数列、三角函数、立体几何、解析几何、概率与统计,这些主干知识是支撑高中数学知识体系的主要内容,构成了数学高考试卷的主体.表3为2009~2013年福建省数学高考试题中解答题考查内容的统计,从中可以看出在稳定的基础上,规避了试题的编排模式. 表3 2009~2013年福建省数学高考理科试题中解答题考查内容的统计 仅在试题的题序上做文章还不足以达到规避模式,在知识网络交汇点设计试题,往往能使试题的情境新颖别致,对基础知识的考查达到必要的深度,交汇能将知识、能力与素质融为一体,从而实现规避模式的目的. 高中数学的知识网络交汇点数不胜数,交汇的形式也多种多样,由此产生的试题更是精彩纷呈.通常知识的交汇可以在2个或2个以上不同的知识模块之间实现,即以一个知识模块为载体,考查其他模块的知识,也可以是同一知识模块内的不同知识点之间的交汇.前者由于知识的内容反差较大,常使得试题的呈现形式新颖别致,出乎预料的交汇形式容易引起人们的注意;而后者的交汇形式较为隐蔽而不显山露水,有时题目看似传统,但可能所蕴涵的数学思想方法却十分深刻. (1)求函数f(x)与g(x)的解析式. (3)求实数a与正整数n,使得F(x)=f(x)+ag(x)在(0,nπ)内恰有2 013个零点. (2013年福建省数学高考理科试题第20题) 分析本题以三角函数为载体,与数列、导数进行交汇.不同知识模块的交汇使本题新颖别致,特别是其压轴题的角色更使其成为亮点,外在的交汇形式只是其一.在第(2)小题探究3个数成等差数列的过程中,需要考生对3个数的大小进行辨析,从而优化解题过程,考查考生思维的简捷性,同时较好地考查了考生的运算求解能力;第(3)小题先研究函数在一个周期内图像的性态,再从特殊到一般解决问题,综合地考查了考生的抽象概括能力、推理论证能力和运算求解能力,这些都使本题熠熠生辉. 2013年福建省数学高考试题给了我们许多启示,将促使我们进行更多地教学反思. [1] 数学课程标准研制组.普通高中数学课程标准(实验)解读[M].南京:江苏教育出版社,2004:288-292. [2] 宋建华.高中数学主干知识考查的六个关键词[J].中小学数学:高中版,2012(7/8):70-72.5 规避模式成为主基调



