当“偶然”邂逅“必然”
——圆锥曲线的一个优美性质
●
(温州中学 浙江温州 325014)
当“偶然”邂逅“必然”
——圆锥曲线的一个优美性质
●林庆望
(温州中学 浙江温州 325014)
1 问题的提出
笔者提供给学生的训练题中,有这样一道填空题:
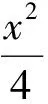
本题看起来很简洁,但做起来并不容易.在上课分析该题时,笔者抽取了几个学生,询问了他们求解此题的思路,学生几乎都用特殊法,即:
当点A为椭圆右焦点时,根据椭圆对称性,得|FN|=|MA|.由椭圆定义可知,

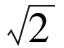
2 问题的延伸
很多数学问题往往在特殊数字中蕴含着一般规律,这在解析几何中显得尤其突出.
解设FA的中点坐标为(x0,0),M(x1,y1),N(x2,y2),则圆的方程为
(x-x0)2+y2=(x0+c)2.
与椭圆方程联立方程组
得
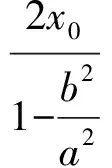
由椭圆的焦半径公式可得
|FM|+|FN|= (ex1+a)+(ex2+a)=

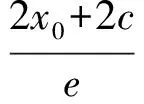
而
|FA|=2x0+2c,
因此

于是得到一个优美的性质:
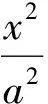

这时候学生终于如释重负,露出舒心的笑容.此时又有学生提出了新的想法:在双曲线和抛物线中是否也有这样结论呢?这种类比的思想很合理.课后笔者还是继续刚才的思考,得出更一般的结论和更简洁的证明.
3 问题的解决

图1 图2 图3

证明(以椭圆为例)以焦点F为极点,建立极坐标系.记|FA|=d,M(ρ1,θ1)N(ρ2,θ2)分别是椭圆与圆的公共点,于是
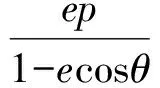
即
decos2θ-dcosθ+ep=0,
从而

又因为在圆中△FMA与△FNA都是直角三角形,所以
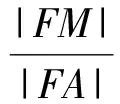
因此
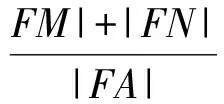
4 感悟
数学教育家波利亚曾说过:“好问题同蘑菇类似,它们都成堆地生长,找到一个以后,你应当在周围找一找,很可能附近就有好几个.”在平时课堂教学中,意外的生成往往是不可多得的教学素材,教师千万不可错过这个探究知识的契机,帮助学生挖掘出更多的“蘑菇”.教师不仅要和学生一起找到问题的答案,更要让学生知道问题的一般规律即数学本质.正确认识必然性与偶然性的辩证关系对学习和研究数学有重要的指导意义,特别在新课改理念指引下,教师要培养学生透过大量偶然性的表面现象去揭示其中蕴含的一般规律,由现象认识本质,由个别到一般,由经验上升为理论,这一点在新课改中显得尤其重要.

