例说如何巧“挖”三角问题中的隐含条件

●

(镇海中学 浙江宁波 315200)

例说如何巧“挖”三角问题中的隐含条件

●胡勇

(镇海中学 浙江宁波 315200)

在解有关三角的问题中，许多学生出现增解和错解.其原因不是不会解答这些题目，而是没有充分挖掘隐含条件.如何充分挖掘三角问题中的隐含条件，从哪里“挖”，怎么“挖”，学生往往感到困惑和迷茫.对此，笔者根据自己多年的教学实践，通过对以下几个典型例子的剖析，并以此抛砖引玉，谈谈如何巧“挖”三角问题中的隐含条件.

1 全面深入审题，挖掘题设隐含条件

例1在△ABC中，内角A,B,C所对的边分别是a，b,c,且sinC=2sinB，求函数

的值域.

(2013年宁波市高三“十校”联考数学试题)

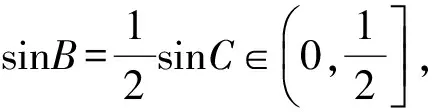
而

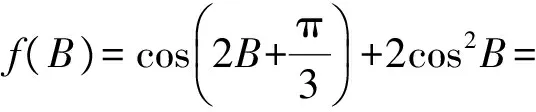
则

于是

从而

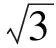
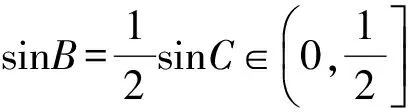
sinC>sinB,

从而

C>B,

得

又因为

所以

正解在△ABC中，因为sinC=2sinB>0，所以

sinC>sinB.

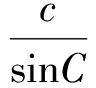
又因为

所以

从而

得

于是

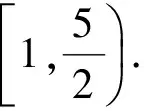
2 掌控解题过程，挖掘转化隐含条件

例2若3sin2α+2sin2β-2sinα=0，则cos2α+cos2β的取值范围是

( )

(2013年浙江省镇海中学《数学(必修5)》模块评价考核试题)

cos2α+cos2β= 2-sin2α-sin2β=

又因为

|sinα|≤1，

所以

故选A.

cos2α+cos2β= 2-sin2α-sin2β=

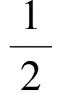
故选D.

3 审视解题结果，挖掘题目隐含条件

例3已知0<α<β<γ<2π,且sinα+sinβ+sinγ=0，cosα+cosβ+cosγ=0，则β-α的值为________.

(2013浙江省镇海中学《数学(必修4)》“三角恒等变换”单元练习题)

错解由条件得

sinα+sinβ=-sinγ，cosα+cosβ=-cosγ，

两式平方相加，得

2+2cos(α-β)=1，

于是

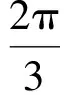
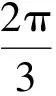
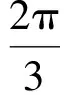
则

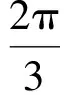
正解由条件得

sinα+sinβ=-sinγ，

cosα+cosβ=-cosγ,

两式平方相加，得

2+2cos(α-β)=1，

于是

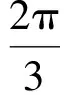
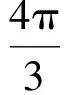
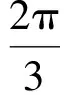
则

这与题设条件矛盾.于是

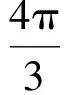
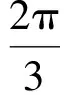
以上是笔者总结的在处理三角问题中对隐含条件挖掘应该注意的地方.我们只要在解三角问题过程中引导学生注意到以上3个方面，并能够举一反三，且在解题的审题、解答过程和结果等各个环节都具有挖掘隐含条件的意识，就能够大大提高解三角问题的准确性、严密性和严谨性，进而发展智力、锻炼思维、提高能力.

[1] 胡勇.一个不容忽视的问题——隐含条件的挖掘[J].数学通讯,2002(14/16):83.

[2] 波利亚.怎样解题[M].涂泓,冯承天,译.上海:上海科技教育出版社,2002:35-38.

[3] 戴再平.数学习题理论[M].上海:上海教育出版社,1991:147-161.