偏振状态下微粒的Mie散射特性研究

杨 颖，黄竹青，2，曹小玲

(1.长沙理工大学能源与动力工程学院，湖南长沙410110;2.湖南有色金属职业技术学院，湖南株洲412006)

1 引言

随着激光技术和计算机的飞速发展，光学法微粒粒度测量技术在越来越多的领域中出现，其中很大一部分是以光散射理论为基础。Mie散射理论是研究各向同性的球形粒子光散射的基础，又称为大粒子弹性散射，其适应范围从几纳米到几毫米甚至更大的气体、液体和固体，如空气中的一些气体分子、硫氧化物分子、雾、云、汽轮机中的水滴等。针对球形粒子，本文利用Matlab软件，选取合适Mie散射计算方法，对散射强度函数、相函数等进行了编程计算和分析。

2 球形粒子散射理论计算

Mie散射理论计算非常复杂，特别是Mie系数的计算，不少国内外学者对算法进行了研究改进，并发表了若干种方法［1－5］，本文采用的是一种比较稳定且精度高的算法，具体见2.2。

2.1 散射强度函数

根据Mie散射理论，当入射光是平面偏振光时，总散射光强的垂直分量Ir和平行分量Is表达式如下(φ是极化角):

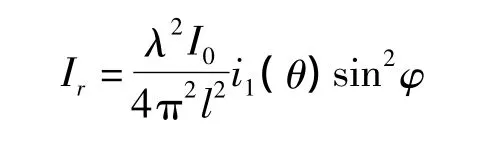
总散射光强表达式为:

当入射光为非偏振光时总散射光强为:

其中，d是观察点与微粒的距离;i1(θ)和i2(θ)是散射强度函数;S1(θ)和S2(θ)是振幅函数，它们之间的关系如下:

由以上公式可知，总散射光强IS、散射强度函数i1(θ)、i2(θ)和振幅函数 S1(θ)、S2(θ)都是 Mie系数an和bn、散射角分布函数πn和τn的无穷级数(关于截止阶数nstop的确定在本节末给出)。所以只要计算出Mie系数an和bn、散射角分布函数πn和τn即可。

2.2 Mie系数的计算

Mie散射系数的计算方法中，用定义式计算比较困难，且非常耗时，所以一般采用基于定义式改进的向前或向后递推算法。而当颗粒吸收性很大或者折射率虚部绝对值非常大时，向后递推计算有可能超过计算机允许的范围而溢出，因此本文采用向前递推算法，根据文献［6］对Mie系数的重新构造进行计算，改进后的Mie系数表达式如下:

其中:

3)执行情况检查(C)：在成本控制执行过程中，实时收集和掌握成本控制数据和信息，对成本控制执行情况进行动态分析和前景预测，对执行情况进行绩效考核和激励，动态和前瞻性地监控成本管理的进展，确保项目投资在成本控制总目标内进行。

其中，α=2πr/λ 是无因次粒径参量;β=mα，m 是微粒相对于周围环境的折射率。

求 Mie系数 an和 bn转化为计算 An(α)、Bn(α)、Ln(α)、Ln(β)。An(α)和 Bn(α)可以用向后递推计算，递推公式如下:

Ln(x)采用向前递推法计算，递推公式为:

由Lentz的连分式算法求初始值 Ln*(x)［7］，具体算法如下:

根据Lentz的证明:

通过计算比较Gnk与Gn(k－1)之差的绝对值满足误差要求，计算截止，再将Gnk代入公式(11)得到Ln*(x)。

散射角分布函数πn和τn同样采用递推方法求(其中θ是散射角):

初始值:π0=0;π1=1;π'0=π'1=0

图1 截止阶数的选取方法Fig.1 Selection method of cutoff number(r=2μm)

3 特性分析

散射光强的分布主要和无因次参量α、折射率m和散射角θ有关，散射(消光、吸收)系数和无因次参量α、折射率m有关，微粒群的散射特性还和分布模型有关，因此本文主要针对这几个参数进行分析。而入射光波长λ的变化相当于无因次参量α的变化，所以改变波长相当于改变α。

3.1 散射强度函数

单个微粒的散射强度函数i1(θ)和i2(θ)表达式如公式(4)。结合Mie系数和角度分布函数进行编程计算，得到散射强度的分布关系，如图2，前向散射明显强于后向散射，且微粒半径越大越明显，散射光强大部分集中在前向小角度范围内，这被称为米氏效应;图2(a)为不同微粒大小之间的对比，散射光强呈现振荡现象，随着微粒半径的增大，振荡越明显。图2(b)为不同折射率之间的对比。由于耗散介质的吸收，散射光强明显比非耗散介质弱，振荡现象随着折射率虚部绝对值的增大逐渐消失，变得平滑，尤其是后向散射。

图2 散射强度随角度分布关系Fig.2 The distribution of the scattering intensity varies with the Angle

3.2消光系数、散射系数和吸收系数

在非耗散介质中，折射率是一个实数，表示没有吸收;在耗散介质中，复折射率m=n+iη，n反映了介质的散射特性，η反映了介质的吸收特性。消光系数和散射系数的计算公式分别如下:

通过Matlab对公式(14)进行计算得到各个系数和微粒大小的关系，如图3。非耗散介质比耗散介质系数曲线振荡明显，曲线有一系列的极大值和极小值，并出现微小的毛刺现象，折射率实部越大，毛刺现象也越明显，极大值和极小值在同一粒径范围内增多，消光系数趋近于2的速度越快;而对于折射率虚部不为0的耗散介质，系数随粒径变化的振荡减弱，毛刺现象消失，曲线变得平滑。当折射率虚部增大，即微粒的吸收特性增强时，系数曲线变得非常光滑。图3(c)中给出了消光系数，散射系数，吸收系数的关系，当颗粒为非耗散介质时，吸收系数Qabs=0，Qext=Qsca;当颗粒为耗散介质时，Qext=Qsca+Qabs。

图3 各系数和微粒大小的关系Fig.3 Relation of the each coefficient and the particle size

3.3 散射相函数

光在某个给定方向单位立体角中散射的能量和所有方向上平均单位立体角中的散射能量之比，称为散射相函数。它表示距离粒子很远处的散射能量随角度分布状况［9－11］。当入射光为平面偏振光时，单个水滴相函数的表达式为:

对于单个微粒，散射系数相当于一个常数，其特性与散射强度函数相似。图4给出了单个水滴的散射相函数和散射角的关系。

图4 单个粒子的散射相函数Fig.4 Scattering phase function of single particle

在研究非单一分散系的散射特性时，假设微粒群中的各个微粒是相互独立的散射体，即各个粒子之间的散射光互不相关，所以微粒群的散射特性是各个微粒散射特性的线性叠加。本文以适合描述破碎形成的微粒群的Rosin－Rammler分布函数表示微粒群尺寸分布，其尺寸分布概率密度函数表达式为:

其中，K是分布参数;珋r是质量中间半径，它表示大于质量中间半径的颗粒数占50%，散射相函数与微粒群的数密度无关［12］，得到粒子群的相函数表达式为:

散射相函数满足归一化条件:∫P(θ)dθ=1

又有散射能量累积分布函数:

表示散射角小于φ的散射能量占所有散射光的比例，因此有:F(π)=1。

图5 微粒群散射相函数Fig.5 Scattering phase function of particle swarm

通过软件对公式(17)进行数值积分，得到微粒群散射相函数与散射角的关系，如图5。微粒群的光散射分布在前向比较平滑，后向小角度出现振荡，与图4单个球形微粒的散射特性比较，振荡明显减弱。分别对不同的分布参数进行计算、对比，不同的分布参数对散射相函数的影响比较小，如图5(a);不同微粒大小对散射光的分布的影响如图5(b)，与单个微粒相比，不同质量中间半径之间的差别减小，特别是在前向30°～60°之间。

4 结论

利用改进后的递推方法求Mie系数，使计算速度大大的提高，而采用Lentz的连分式方法使计算结果更加精确。针对球形微粒，入射光为平面偏振光，本文分别对单个微粒和微粒群的散射特性进行了计算分析，对比各个参数对散射强度函数、散射相函数、散射(吸收、消光)系数等的影响，对光散射实验研究具有指导作用，有助于对实验数据的分析。

［1］ V DAVE.Scattering of visible light by large water sphere［J］.Appl Opt，1969，8(2):155 －161.

［2］ Wang Shimin，Zhu Zhen，Ye Mao，et al.Two improved numerical algorithms of mie theory in the particle sizing by light scattering method［J］.Acta Metrologica Sinica，1999，20(4):279 －285.(in Chinese)王式民，朱震，叶茂，等.光散射粒度测量中Mie理论两种改进的数值计算方法［J］.计量学报，1999，20(4):279－285.

［3］ Wang Lianfen，Liu Guangbin，Zheng Zhong，et al.Onwards continued fraction algorithm for Mie scattering and numerical simulation［J］.Optical Technique，2009，35(4):541 －543.(in Chinese)王莲芬，刘光斌，郑重，等.Mie散射向前递推连分式算法及其数值模拟［J］.光学技术，2009，35(4):541－543.

［4］ Wang Shaoqing，Ren Zhongjing，Zhang，Ximing，et al.New algorithm of mie scattering parameters［J］.Laser Journal，1997，18(3):9 －13.(in Chinese)王少清，任中京，张希明，等.Mie散射系数的新算法［J］.激光杂志，1997，18(3):15 －22.

［5］ 蔡小舒，苏明旭，沈建琪，等.颗粒粒度测量技术及应用［M］.北京:化学工业出版社，2010.

［6］ Shen Jianqi，Liu Lei.An improved algorithm of classical Mie scattering calculation［J］.China Powder Science and Technology，2005，11(4):1 －5.(in Chinese)沈建琪，刘蕾.经典Mie散射的数值计算方法改进［J］.中国粉体技术，2005，11(4):1 －5.

［7］ W J Lentz.Generating bessel funtions in Mie scattering calculations using continued fractions［J］.Appl Opt，1976，15:668 －671.

［8］ Wiscombe W J.Improved Mie scattering algorithms［J］，Applied Optics，1980，19:1505 －1509.

［9］ Zhang Heyong，Ren Deming，Zhao Weijiang，et al.Research of scattering phase function of spheric particle under polarized state［J］.Opto － Electronic Engineering，2008，35(9):70 －75.(in Chinese)张合勇，任德明，赵卫疆，等.偏振状态下球形粒子的散射相位函数研究［J］.光电工程，2008，35(9):70－75.

［10］ Yuan Yijun，Ren Deming，Hu Xiaoyong.Computing scattering phase function by recursive formula of Mie Theory［J］.Chinese Journal of Light Scattering，2005，17(4):366 －371.(in Chinese)袁易君，任德明，胡孝勇.Mie理论递推公式计算散射相位函数［J］.光散射学报，2005，17(4):366 －371.

［11］ Du Zhufeng，Lu yimin，Huang Tiexia.The approximate calculation of scattering phase function［J］.Journal of Optoelectronics·Laser，1998，9(5):422 － 425.(in Chinese)杜竹峰，卢益民，黄铁侠，等.散射相位函数的近似计算［J］.光电子·激光，1998，9(5):422 －425.

［12］ Huang Zhuqing.Investigation of exhaust wetness measurement method in steam turbine based on mie scattering of laser［D］.Changsha:National University of Defence Technology.2010.1.(in Chinese)黄竹青.基于光散射的汽轮机湿蒸汽特性测量方法研究［D］.长沙:国防科技大学，2010.