起爆点位置对战斗部爆炸破片特性的影响

孔祥韶，吴卫国，杜志鹏，李俊，李晓彬

(1.武汉理工大学交通学院，湖北武汉430063;2.海军装备研究院，北京100161)

典型的半穿甲内爆式反舰武器对舰船结构的毁伤效应包括自然破片和冲击波.从这2种载荷特性来看，爆炸冲击波对结构的破坏作用主要与战斗部装药量以及所在舱室的结构尺寸有关［1-2］;而战斗部爆炸产生的破片具有极强的穿透性，其空间分布直接影响结构的破坏模式.在战斗部壳体形成的破片特性研究方面，Mott［3］建立了理论分析模型，给出了破片大小分布以及速度计算的相关公式.此后，随着理论分析模型的逐渐完善和试验技术发展，学者们研究了破片的形成机理、形状及质量分布的简化模型和计算方法［4-7］.在前人提出的计算模型中，对圆柱形战斗部的分析均做了一定的简化，并未考虑战斗部端部封盖对爆炸破片分布和速度的影响.近年来，也有一些学者［8-9］对战斗部爆炸形成破片过程及特性进行了相关的数值计算工作.数值计算方法已成为战斗部破片特性分析的辅助手段.

本文采用非线性动力分析程序ANSYS AUTODYN 14.0和基于Mott分布理论的Stochastic随机模型，采用光滑粒子动力学方法(smoothed particle hydrodynamic，SPH)对圆柱形战斗部爆炸形成自然破片的过程进行了三维数值计算研究，分析了端点起爆和中心点起爆工况下圆柱形战斗部壳体爆炸破片的空间分布及速度特性.

1 数值计算模型及材料参数

1.1 SPH方法

SPH方法是一种自适应、无网格粒子形式，具有拉格朗日性质的数值模拟方法，避免了网格畸变等问题，适用于处理大变形及冲击载荷等问题［10-11］.该方法被广泛应用于含能材料的爆轰、爆炸冲击波的传播及材料侵彻模拟等方面［12-14］.SPH方法适用于计算类似金属壳体膨胀碎裂的过程.SPH方法是用来求解流体动力学问题中基于密度、速度、动量、能量等变量场的偏微分方程组的.SPH方法定义的质量、动量和能量守恒方程［15］如下:

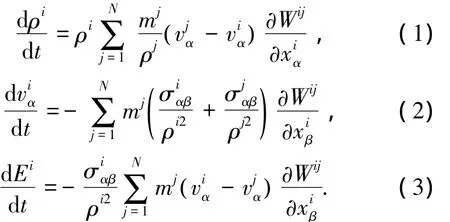
式中:Wij=(Wxi-xj，h)光滑核函数;h是光滑长度，用来定义光滑核函数的影响区域;t代表时间;x表示空间坐标;ρ为密度;va为速度分量;σαβ是应力分量;E为比内能，下标α(α=1，2，3)和β(β=1，2，3)为分量指标.

采用SPH方法计算金属壳体的膨胀至破裂过程中，在壳体裂纹扩展及碎片运动过程中可能会出现应力不稳定现象.本文在数值模拟过程中进行了多次数值试验，以文献［16］给出的建议和计算稳定准则作为参考，避免在计算过程中出现应力不稳定现象.

1.2 数值计算模型

本文数值计算的对象为试验中采用的战斗部模型，试验模型为圆柱形带壳战斗部，圆柱形壳体的内径为110 mm，高度为160 mm，厚度为6 mm，战斗部壳体重量为4.10 kg;壳体材料为低碳钢，壳体内装有TNT炸药，装药量为1.9 kg.战斗部一端封盖中部设置雷管安装开孔，通过雷管引爆主装药.圆柱形战斗部模型实物如图1所示.

图1 圆柱形战斗部模型Fig.1 Model of cylindrical warhead

根据圆柱形战斗部的对称性，只建立其1/4计算模型，如图2所示.由于基于网格算法的数值计算来分析战斗部的爆炸过程，在模拟破裂过程时一般是通过删除失效单元后形成破片，而失效单元被删除后，破片特征失真比较严重，用SPH算法模拟材料断裂损伤可以改进因删除单元而造成的破片形状失真［17］.本文的数值模拟研究采用显式动力有限元程序Ansys Autodyn 14.0，炸药和战斗部壳体用SPH粒子离散，通过多次数值试验将粒子大小取为1 mm，1/4计算模型共有513 192个粒子，计算过程采用8个并行模块.数值计算分为2种工况，分别是端点起爆工况和中心点起爆工况.

图2 圆柱形战斗部1/4计算模型Fig.2 1/4 computational model of cylindrical war-head

1.3 战斗部壳体材料本构方程及破坏准则

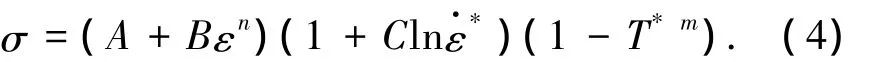
战斗部壳体材料为Q235低碳钢，其本构方程用 Johnson-Cook［18］模型:式中:σ表示等效应力;ε表示等效应变，=ε·/ε·0表示无量纲的塑性应变率，取ε·0为准静态实验的应变率;T*=(T-Tr)/(Tm-Tr)，Tr为参考温度，Tm为材料的熔点温度;A、B、C、n、m为与材料有关的实验参数.

材料的随机破坏模型采用AUTODYN程序中的Stochastic模型，采用Mott分布表征物质的固有缺陷来产生破坏和裂纹的模型，在材料离散化模型内随机添加一些弱化点，这样可描述适用不同分布的Stochastic模型时的离散几何体模拟真实材料的破坏模式，根据不同分布得到不同数量和大小的破片［9］.

根据［3］分布理论，在AUTODYN程序中通过给定失效应力或应变得到材料断裂的平均应变ε0.对于钢壳体［9］，C=0.046 7.本文计算中将低碳钢壳体的最大失效应变取为0.3，γ取为57.

1.4 炸药状态方程

壳体内的装药采用JWL状态方程，其压力形式表示为

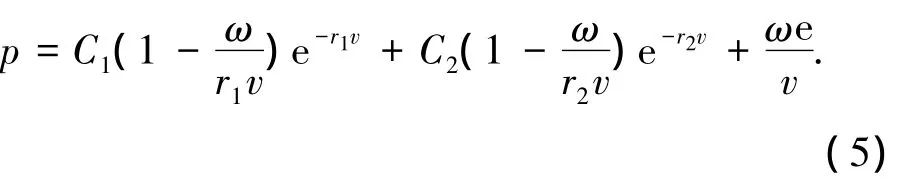
式中:C1、C2、r1、r2为常数，取 AUTODYN 材料库中的默认值.

2 圆柱形壳体形成破片过程

2.1 圆柱形壳体的膨胀和破裂

2.1.1 端点起爆

战斗部壳体在内部装药作用下膨胀和破裂的过程如图3所示.在内部压力作用下，战斗部壳体接近起爆点的部分首先发生膨胀，端部封盖鼓起变形，如图3(a)、(b).当t=5.30×10-2ms时，靠近起爆点的端部封盖已从壳体上撕裂，并且封盖中部鼓起变形增大.圆柱形壳体靠近起爆点部分膨胀半径较大，出现沿高度方向上的裂纹，远离起爆点的端头封盖也出现鼓起变形，如图3(c).随着内部压力的持续作用，远离起爆点的端头封盖也从壳体上撕裂并飞出，端头封盖与壳体连接部位处出现大量碎片.圆柱形壳体出现沿高度方向上的贯穿裂纹并进一步膨胀，如图3(d)所示.

根据爆轰波在壳体内部传播过程的分析，远离起爆点的壳体和端头封盖受到初始爆轰波和壳体反射波的作用，其变形速度明显大于靠近起爆点的壳体，相比而言，圆柱形壳体膨胀半径出现了大小倒置的情况，即远离起爆点的圆柱形壳体部分膨胀半径大于靠近起爆点的壳体膨胀半径，且二者之间的差值有进一步增大的趋势，圆柱形壳体沿高度方向不同位置处出现膨胀速度差.从端头封盖的变形来看，远离起爆点的端部封盖的速度也明显较大.战斗部壳体和端头封盖的进一步膨胀过程如图3(e)～(h)所示.

从破片的产生和分布情况来看，壳体膨胀过程中首先在靠近起爆点的端头封盖和圆柱形壳体连接处产生破片，其主要原因是该位置处存在变形不连续和速度差，即端头封盖在受到壳体内部压力作用下变形的趋势方向是沿其法向，而圆柱形壳体的变形趋势是沿壳体径向.在远离起爆点的端头封盖和圆柱形壳体的连接处的情况也大致相同，该位置形成了大量的小质量碎片.圆柱形壳体上首先出现了沿高度方向的裂纹，破片最初在接近起爆点的壳体顶部位置出现，随着壳体膨胀过程中沿高度方向上速度差的出现，在高度方向上连续的壳体间出现断点，随着膨胀的加剧破片的数量也逐渐增加.

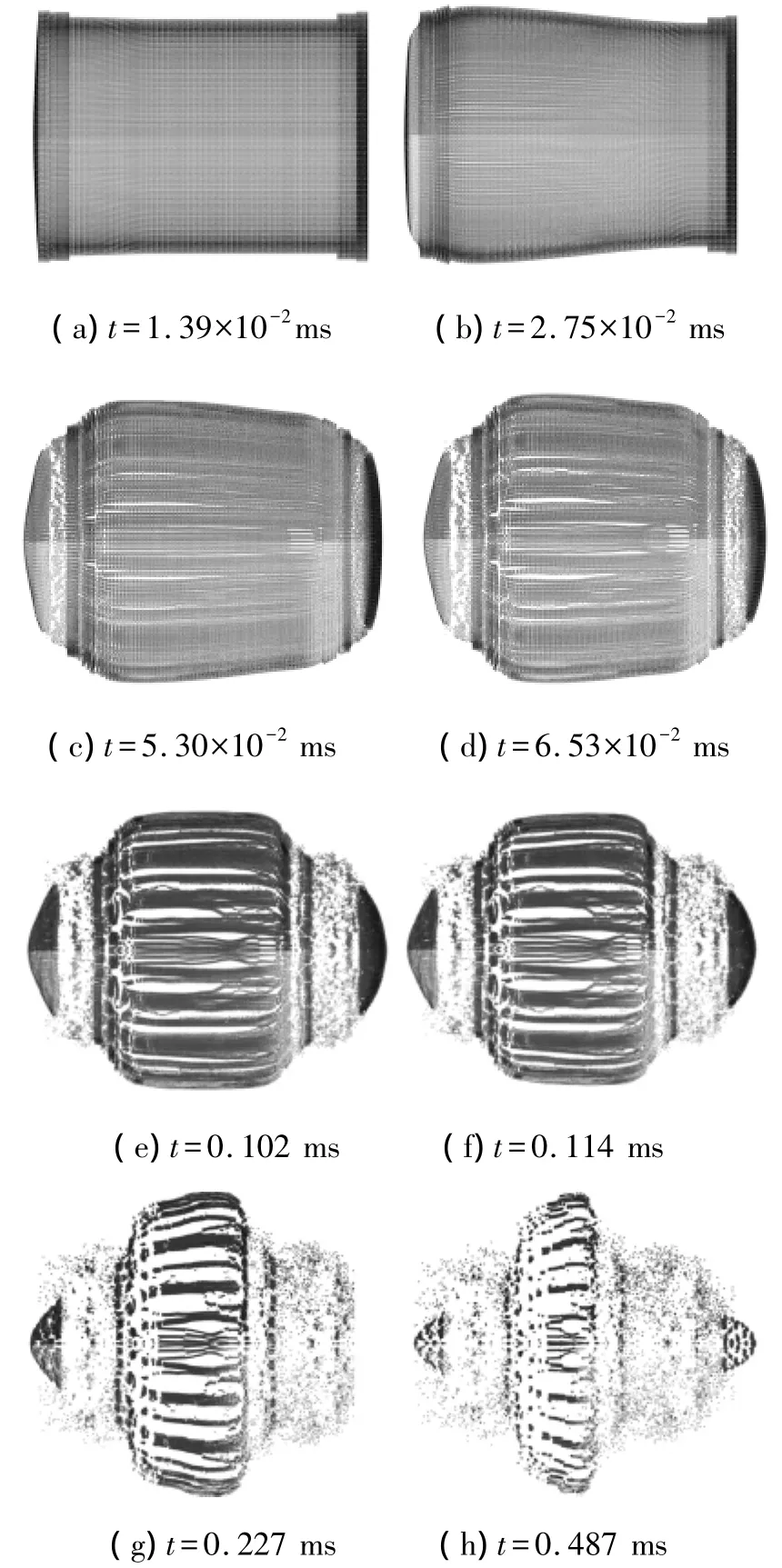
图3 战斗部壳体的膨胀和破裂过程-端点起爆Fig.3 The expansion and rupture process of warhead case(initiation at one end)

2.1.2 端点起爆

当起爆点在装药中心位置时壳体的膨胀和破裂过程如图4所示.装药起爆后金属壳体中部首先开始膨胀，随着膨胀半径的进一步增大，两端封盖从壳体上撕裂，t=6.55×10-2ms时圆柱形壳体在高度方向上已出现贯穿裂纹，如图4(b).与端部起爆的情况不同，中心点起爆的情况下壳体的膨胀比较对称，两端封盖从壳体撕裂后的速度相同，封盖与壳体连接处形成大量小质量破片，如图4(c)、(d).对于圆柱形壳体，其中部的膨胀速度大于其他位置，而端部由于受到端头封盖的限制膨胀速度明显较小，使得圆柱形壳体在高度方向上从中部到端部的膨胀速度存在梯度，中部壳体形成的破片速度明显较大，从而使圆柱形壳体沿高度方向断裂形成破片，如图4(e)、(f).

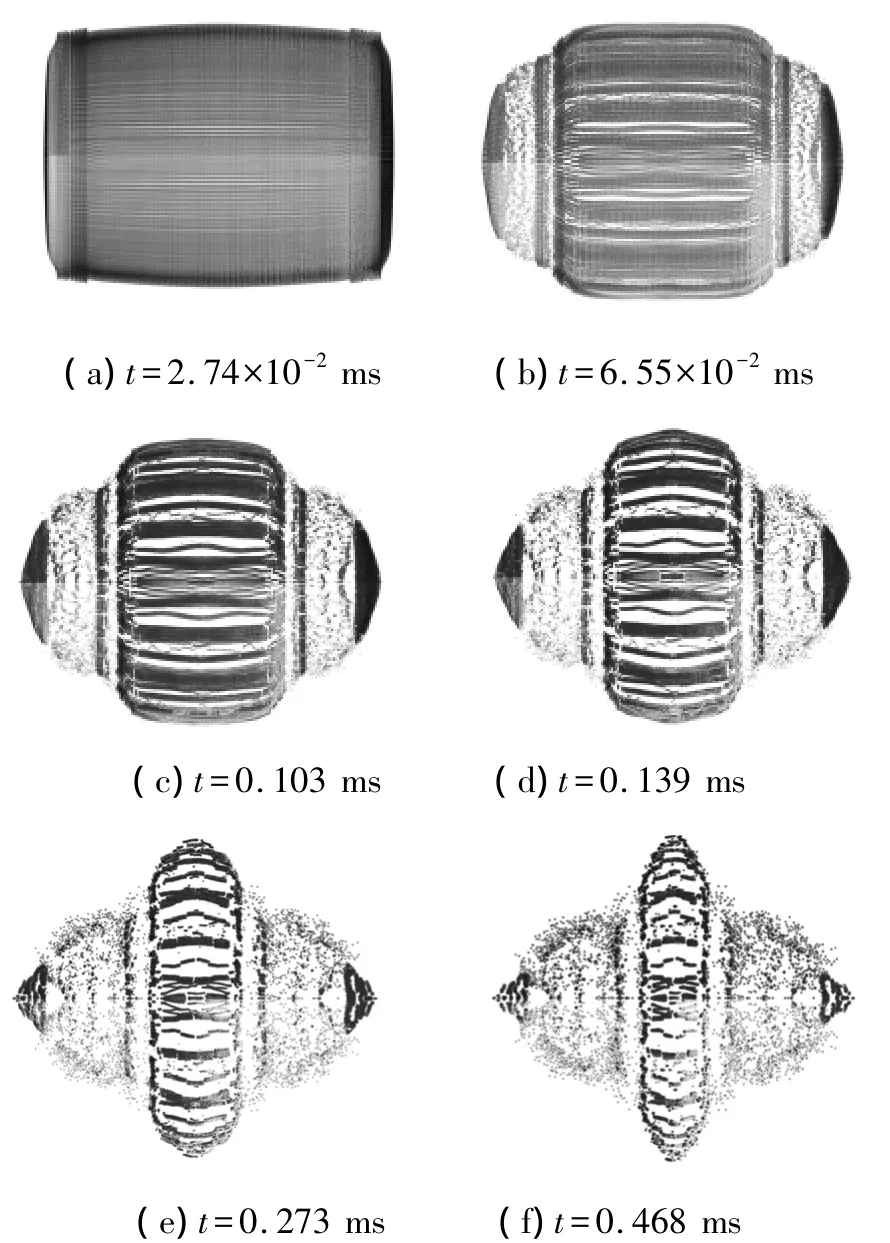
图4 战斗部壳体的膨胀和破裂过程-中心点起爆Fig.4 The expansion and rupture process of warhead case(initiation at the center)

起爆位置不同的情况下战斗部壳体形成的破片分布如图5所示(沿高度方向视图)，总体来看破片主要包括几个部分:圆柱形壳体形成的破片、端头封盖形成的破片、端头封盖、圆柱形壳体相接的地方形成的大量小质量碎片.

从二者的对比来看，端点起爆情况下圆柱形壳体形成的破片分布更加均匀，主要原因是沿壳体高度方向上的膨胀速度从近爆点至远爆点逐渐递增，形成的破片较均匀地分布在膨胀半径的路径上，而中心点起爆时由于壳体膨胀的最大速度在中部，沿圆柱形高度方向上壳体的膨胀速度在中部出现拐点，并且上下对称，使得破片在膨胀半径的路径上分布相对集中.端点起爆情况下端头封盖产生的破片分布范围稍大，破片数量相对较多，大小相对均匀.端点起爆时圆柱形壳体和端头封盖连接处产生的小质量碎片的分布范围更广，而中心点起爆时形成的小质量破片相对比较集中.

在数值计算过程中对战斗部壳体爆炸形成的破片进行统计分析，以起爆后3 ms为统计时刻.端点起爆和中心点起爆情况下壳体产生的破片数量分别为2 768个和3 171个，其中端点起爆时形成的破片的最大质量为33.5 g，主要分布在离起爆点较远的4/5圆柱形壳体处;端部封盖形成的破片质量也较大，最大破片质量为21.6 g，距起爆点较近的封盖和较远的封盖形成的破片质量相差不大.而中心点起爆时壳体形成的破片的最大质量为35.5 g，产生于端部封盖，且质量在18.6 g以上的破片均由端部封盖破碎形成.

图5 起爆位置不同时破片的分布情况Fig.5 The distribution of fragments under the conditions of different initiation point

2.2 壳体膨胀形成破片速度

从2.1节分析可知，战斗部壳体在内部装药爆炸压力作用下膨胀及破裂过程与起爆点的位置有关，壳体上不同位置形成的破片速度差异也较大，为了进一步研究壳体破裂后形成的破片的速度特性，本节将进行更深入的数值计算研究.在数值计算过程中，壳体的两端封盖及圆柱形部分都设置了测点，如图6所示，其中测点1～4布置在离起爆点较近的封盖上，测点5～8布置在圆柱形壳体外表面，测点9～12布置在远端的封盖上.

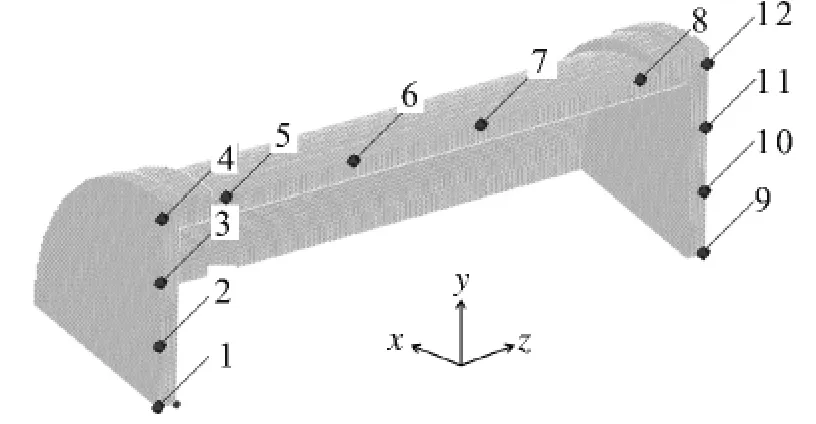
图6 战斗部壳体测点布置Fig.6 Measuring-point arrangement of the case

端点起爆情况下近端封盖测点的速度分布情况如图7所示，其中测点1在封盖中心部位，该测点在Z方向上速度最大，达到1 344 m/s.靠近封盖边缘的测点4在Z方向上速度仅为362.3 m/s，但测点4在Y方向上的速度达到598.8 m/s，说明端部封盖边缘处存在沿圆柱形壳体径向膨胀.这种膨胀的趋势在端部封盖边缘处尤为明显，离边缘稍远处的测点3和测点2在在Y方向上的速度分别为152 m/s和58 m/s，其主要运动方向在端部封盖的法向方向上.远端封盖上的测点的速度分布情况如图8，各测点的速度变化趋势与近端封盖上测点的基本一致(Z向速度反向).但远端封盖处测点的速度较近端封盖测点的更大，测点9的 Z向速度达到1 748.2 m/s，V9Z/V1Z=1.3;测点12的Y向速度达到734.3 m/s，V12Y/V4Y=1.23.

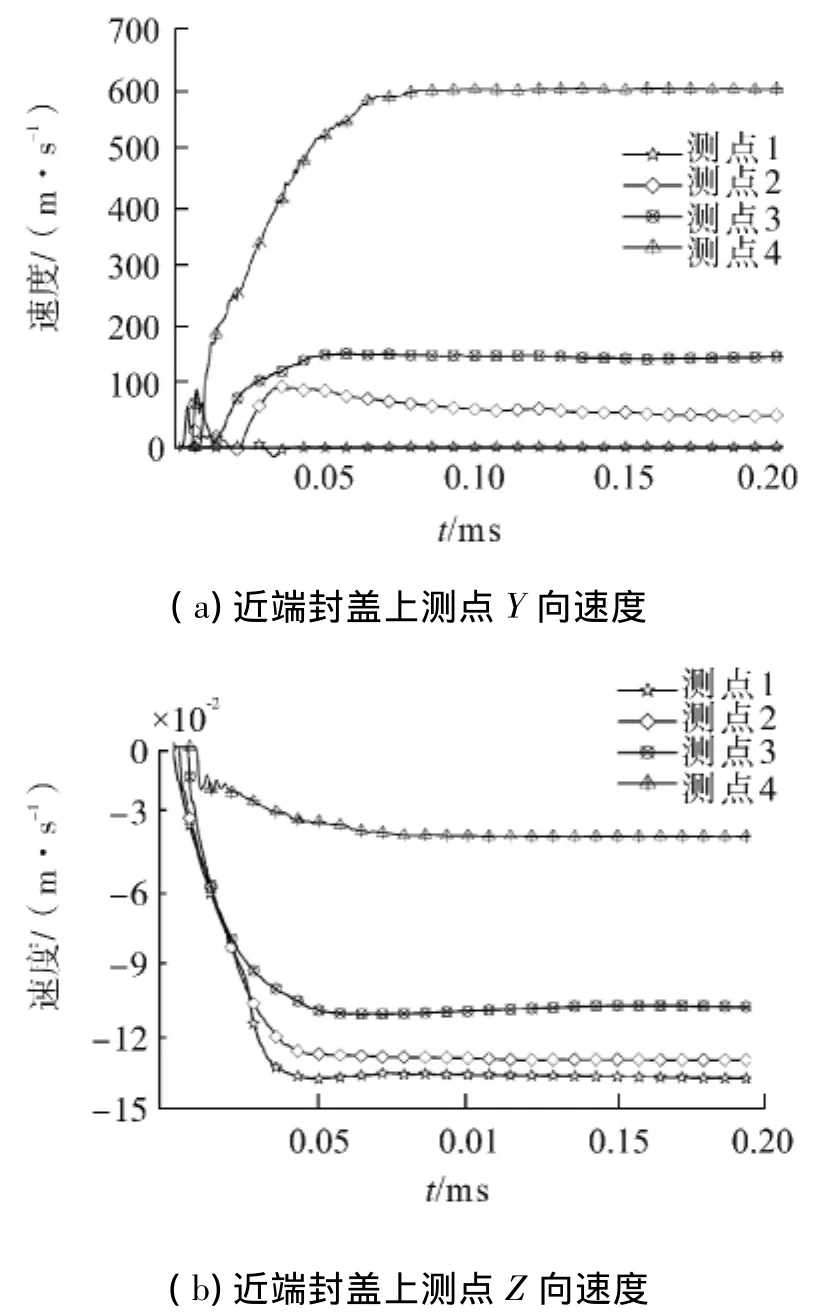
图7 端点起爆时近端封盖测点速度历程曲线Fig.7 Velocity of measuring points on near-end(initiation at one end)

端点起爆情况下圆柱形壳体上测点的速度分布情况如图9所示，各测点Y向速度，即沿圆柱形壳体径向方向的膨胀速度随着距起爆点距离的增大而增加，但测点7和测点8的径向膨胀速度基本一致.从各测点Z向速度的分布来看，测点5出现了沿Z轴负向的速度，达到134.2 m/s，而其他各测点Z向的速度均为正.根据测点5的Z向速度时间历程曲线可以发现，其Z向速度先正后负，这种现象发上的主要原因是:当爆轰波从起爆点向远端传播时，测点5先经历了初始爆轰波的作用，其运动方向沿Z轴正向.而当初始爆轰波从远端壳体上反射后，反射波的运动方向与初始爆轰波的方向相反，在反射波的作用下测点5出现了沿Z轴负向的运动.

中心点起爆时端部封盖及圆柱形壳体上各测点的速度历程曲线如图10所示，由于对称性的存在，两端封盖的测点速度大小一致，方向相反，所以对其速度特性只要分析一端就可以.端头封盖上的速度分布趋势与端点起爆的情况基本相同，壳体边缘处存在较大的沿圆柱壳径向方向的速度.圆柱形壳体上个测点的速度表现出明显的对称性，测点5和6、7和8的Y向速度基本相同，而Z向速度大小基本一致，方向相反.

通过对比不同起爆情况下封盖处测点的最大速度可以发现，端点起爆的情况下远、近端封盖中心位置的测点速度与中心点起爆时该测点速度的比值分别为1 748.2/1 533.2=1.14，1 344/1 533.2=0.88.对于圆柱形壳体上的测点，2种起爆情况下测点5径向膨胀速度比值为1 149.3/1 226.2=0.94;测点7的该比值为1 433.9/1 449.6=0.989.

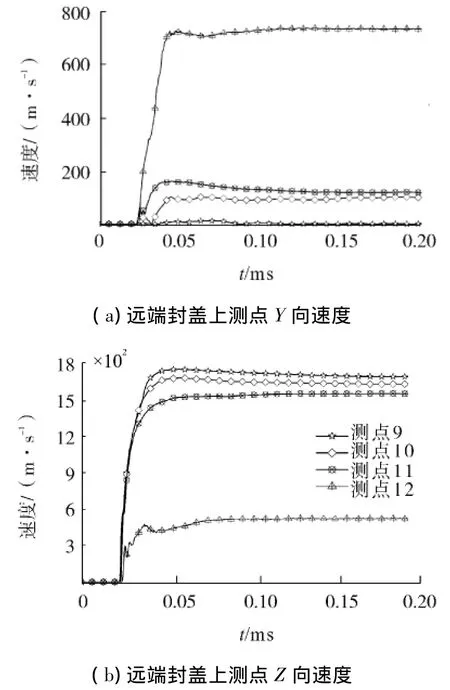
图8 端点起爆时远端封盖测点速度Fig.8 Velocity of measuring points on far-end(initiation at one end)

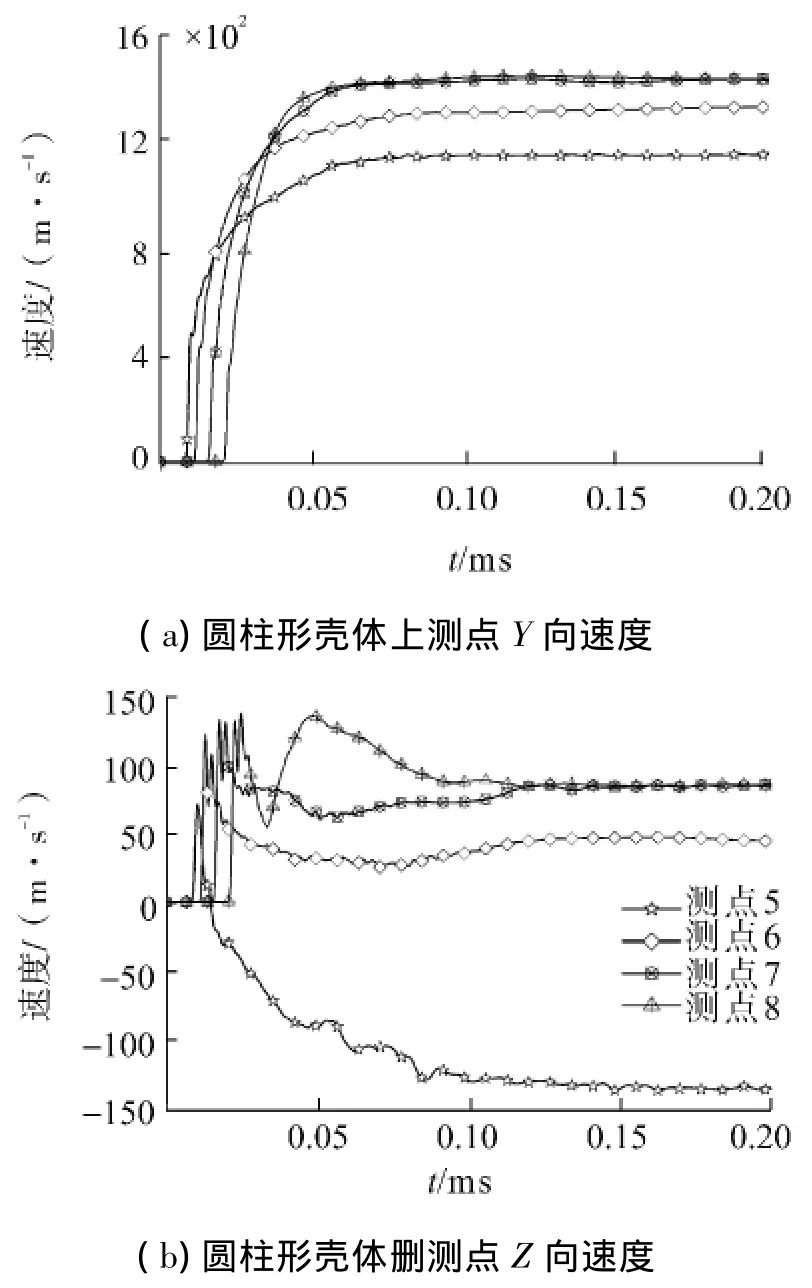
图9 端点起爆时圆柱形壳体测点速度Fig.9 Velocity of measuring points on cylindrical case(initiation at one end)

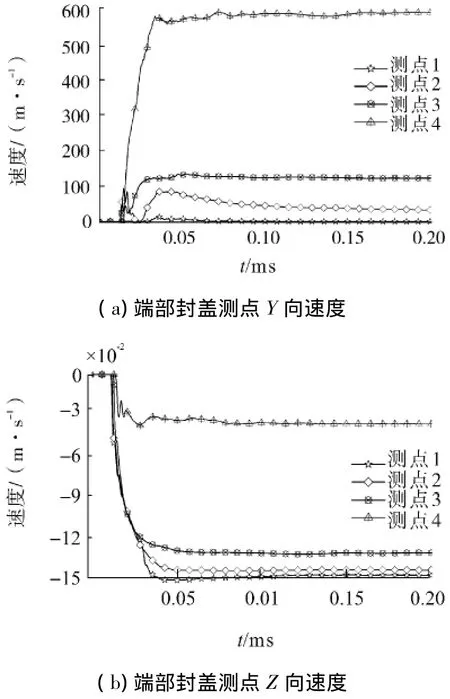
图10 中心点起爆时端部封盖测点速度历程曲线Fig.10 Velocity of measuring points on one end(initiation at the center)

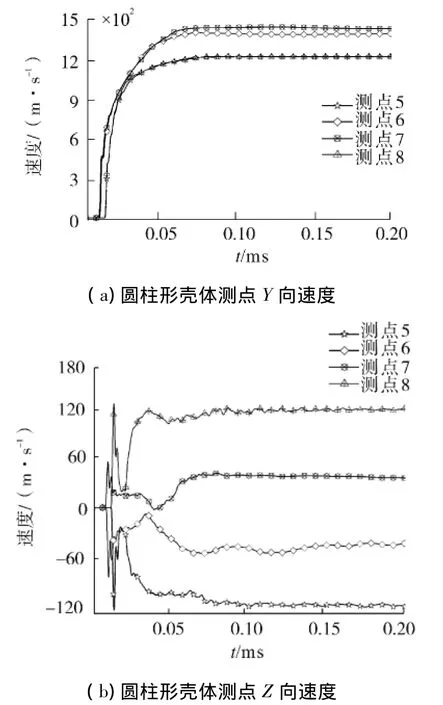
图11 中心点起爆时圆柱形壳体测点速度历程曲线Fig.11 Velocity of measuring points on far-end(initiation at the center)

3 结论

本文采用数值计算方法对圆柱形战斗部爆炸时壳体破裂形成自然破片过程进行了三维数值模拟，对战斗部壳体产生的破片空间分布及速度特性进行了研究，分析了不同起爆位置对圆柱形战斗部破片的空间分布和速度特性的影响.作得到以下几点结论:

1)采用数值计算方法可得到战斗部自然破片的详细分布情况，为结构在战斗部接近爆炸情况下的毁伤分析提供输入载荷.

2)通过对战斗部壳体形成的破片质量特性的分析，端点起爆时形成的大质量破片主要分布在离起爆点较远的4/5圆柱形壳体处;端部封盖形成的破片质量也较大，距起爆点较近的封盖和较远的封盖形成的破片质量相差不大.而中心点起爆时壳体形成的大质量破片均由端部封盖破碎形成.结合破片的质量分布和膨胀速度来分析，大质量破片主要产生于膨胀速度梯度较小的位置.即对于圆柱形壳体，沿高度方向上径向膨胀速度的差异直接影响壳体形成破片的大小.

3)对于典型的半穿甲内爆式反舰武器战斗部，在穿透舰船结构引爆时自身还具有一定的速度，将与爆炸形成的破片的速度产生叠加效应，其对舰船内部结构的威胁更大，在防护设计时应予以重视.

［1］EDRI I，SAVIR Z，FELDGUN V R，et al.On blast pressure analysis due to a partially confined explosion:Iexperimental studies［J］.International Journal of Protective Structures，2011，2(1):1-20.

［2］HU Y，WU C Q，MATTHEW L，et al.Characteristics of confined blast loading in unvented structures［J］.International Journal of Protective Structures，2011，2(1):21-44.

［3］MOTTN F.Fragmentation of shell cases［J］.Proceedings of the Royal Society of London Series A Mathematical and Physical Sciences，1947，189(1018):300-308.

［4］ARNOLD W，ROTTENKOLBER E.Fragment mass distribution of metal cased explosive charges［J］.Int J Impact Eng，2008，35(12):1393-1398.

［5］GOTO D M，BECKER R，ORZECHOWSKIT J，et al.Investigation of the fracture and fragmentation of explosively driven rings and cylinders［J］.Int J Impact Eng，2008，35(12):1547-1556.

［6］HARING I，SCHONHERR M，RICHTER C.Quantitative hazard and risk analysis for fragments of high-explosive shells in air［J］.Reliability Engineering and System Safety，2009，94(9):1461-1470.

［7］ZHOU F，MOLINARI JF，RAMESH K T.An elastic-visco-plastic analysis of ductile expanding ring［J］.Int J Impact Eng，2006，33(1-12):880-891.

［8］TANAPOMRAWEEKIT G，KULSIRIKASEM W.Effects of material properties of warhead casing on natural fragmentation performance of high explosive(HE)warhead［J］.Word Academy of Science，Engineering and Technology，2011，59:1275-1280.

［9］蒋建伟，张谋，门建兵，等.PELE弹侵彻过程壳体膨胀破裂的数值模拟［J］.计算力学学报，2009，26(4):568-572.JIANG Jianwei，ZHANG Mou，MEN Jianbing，et al.Numerical silulation of PELE natural fragments formation［J］.Chinese Journal of Computational Mechanics，2009，26(4):568-572.

［10］LUCY L B.A numerical approach to the testing of the fission hypothesis［J］.Astron J，1977，82(12):1013-1024.

［11］LIU M B，LIU G R.Smoothed particle hydrodynamics(SPH):an overview and recent developments［J］.Arxiv Comput Methods Engrg，2010，17(1):25-76.

［12］JOHNSON G R，STRYK R A，BEISSEL S R.SPH for high velocity impact computations［J］.Comput Method Appl M，1996，139(1-4):347-373.

［13］LIU M B，LIU G R，ZONG Z，et al.Computer simulation of high explosive explosion using smoothed particle hydrodynamics methodology［J］.Computers and Fluids，2003，32(3):305-322.

［14］LIU M B，LIU G R，LAM K Y，et al.Meshfree particle simulation of the detonation process for high explosives in shaped charge unlined cavity configurations［J］.Shock Waves，2003，12(6):509-520.

［15］MONAGHAN J J，GINGOLD R A.Shock simulation by the particle method SPH［J］.JCoPh，1983，52(2):374-389.

［16］SWEGLE JW，HICKSD L，ATTAWAY SW.Smoothed particle hydrodynamics stability analysis［J］.JCoPh，1995，116(1):123-134.

［17］王新征，张松林，邹广平.内部短药柱爆炸作用下钢筒破裂的数值分析［J］.高压物理学报，2010，24(1):61-66.WANG Xinzheng，ZHANG Songlin，ZOU Guangping.Numerical analysis of fragmentation properties of the steel cylinder subjected to detonation of internal short cylindrical explosive charge［J］.Chinese Journal of High Pressure Physics，2010，24(1):61-66.

［18］JOHNSON G R，COOK W H.Fracture characteristics of three metals subjected to various strains，strain rates，temperatures and pressures［J］.Eng Fract Mech，1985，21(1):31-48.