受迫振动实验中几个问题的探讨
郎 江,张锐波
(浙江大学城市学院,浙江 杭州 310015)
在机械制造、建筑工程与配电网络中等都存在着共振现象,其利害兼而有之,由于受迫振动导致的共振现象已引起工程技术人员的极大关注。“共振”现象既有其破坏的一面,也有其利用价值。很多电声器件就是运用了共振原理设计制作,目前,也成为微观科学领域的重要研究手段,诸如利用核磁共振和顺磁共振研究物质结构等。[1-2]
当摆轮受到周期强迫外力矩M=M0cosωt作用,并在有空气阻尼的媒质中运动时,其运动方程为


图1 欠阻尼振幅随时间变化的振动曲线
1 品质因素分析
品质因素是为了描述振动系统在振动中,能量耗散的情况下引入的,它是标志欠阻尼系统的重要物理量之一,其含义为


在欠阻尼条件下,当β≠0,M0=0时,没有强迫力矩,(1)式为欠阻尼振动方程,让(1)式左边为0,其解为,明显满足欠阻尼条件,即

β越小,带宽越窄,振幅频率响应曲线越尖锐。代入(2)式得

这就是说,β越小,Δω越窄,系统的Q值也就越高。可见,Q值越高,意味着系统的抗干扰能力越佳,除非干扰频率很接近共振频率,否则系统是不会有响应的。
2 振动系统的半宽带
强迫力矩对摆轮做功,不断地向振动体传递能量,以补充阻尼振动所消耗的能量,使之振动达到稳定状态,此时,系统的振幅为
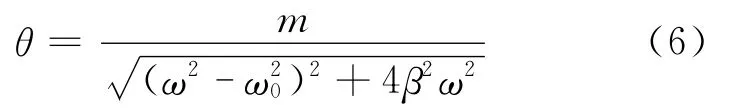
当系统产生共振时,产生的最大振幅

阻尼振动系统对周期性外力有一个响应范围,当我们利用共振系统来选择某种频率振动时,总希望这个频率响应曲线(共振峰曲线)越尖锐越狭窄就越好。


图2 幅频特性曲线与半宽带的关系
当β≪ω0,上式成为
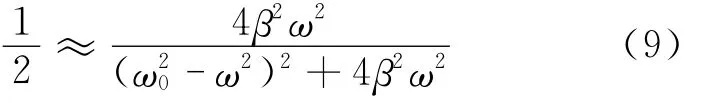
于是就有

即

显然,ω<0的解是不合理的,应该舍去,得到
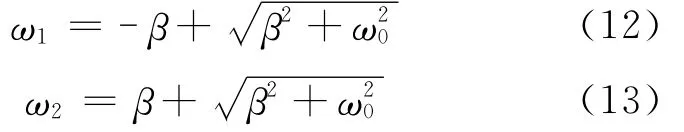
于是
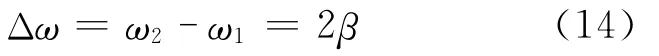
即

明显可以看出,当共振圆频率接近系统固有频率时,阻尼系数β减小,当β2≪时,ω≈ω0,由(2)式知,θr就越大。
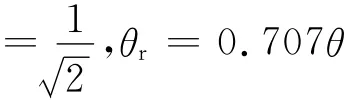
3 稳定受迫振动中强迫力与阻力做功
前面说过,在受迫振动达到稳定状态时,强迫力的功恰恰弥补阻尼所损耗的能量,下面就来证明这个结论。强迫力对系统做功功率为

阻尼力对系统做功的功率为
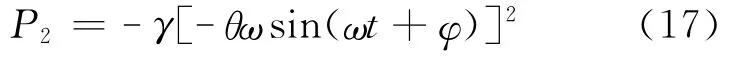
在一个周期(T=2π/ω)内,它们的平均功率分别是

因为稳定受迫振动的初相位满足

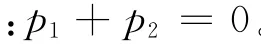
4 结 论
上述受迫振动实验涉及到的几个问题,多数工科院校大学物理及实验教材中几乎没有深入研究或阐述,而恰恰就是这些概念往往会对学生学习相关专业或后期学习影响深远,诸如土木工程、信电和计算机专业等。受迫振动已经成为各类高校力学类重要实验,学生不仅要学会实验操作、数据采集和处理,还应对实验所涉及的数学模型、相关物理量的理论推导进行深入研究。这样做有利于培养学生的应用创新能力和综合素质提高。
[1] 张锐波等.受迫振动实验理论研究与探讨[J].全国大学物理论坛会议论文集,2009,6.
[2] 张岩文等.利用又阻尼振动测液体粘滞系数实验研究[J].大学物理实验,2012,05:35-37.

