基于样本熵的阿城站月径流序列复杂性分析
张玉国
( 黑龙江省水文局,哈尔滨150010)
0 引 言
水文系统是一个复杂系统,又是一个动态的非线性复合系统[1]。在自然环境和人类活动的强烈干扰下,河川径流呈现出高度的复杂性和非线性。对径流序列进行复杂性分析,可以反映区域水文系统影响因子的数量多少,可以充分挖掘其内在信息与联系,是认识水文系统动态演变特征的重要途径。目前,复杂性测度方法主要有分形理论[2]、符号动力学[3]、混沌理论[4]、C1和C2复杂度[5]、涨落复杂度[6]等。但或多或少存在着所需数据量大、抗噪声能力弱等缺点。有些水文时间序列的长度可能较短,所以十分需要用较短数据就能有效测度序列复杂性特征的算法。2000年,Richman J S 等[7〛提出了样本熵,它具有计算不依赖数据长度、较高一致性、对缺失数据不敏感等优点[8],是一种较好的时间序列复杂性测度方法,已经广泛地应用于各个领域。因此,本文采用样本熵方法对阿城站多年月径流序列的复杂性特征进行测度,从而揭示其动态变化规律,以期为流域水资源的合理配置提供科学依据。
1 研究方法与研究区域
1.1 研究方法
样本熵是一种有别于近似熵的不计入自身匹配的统计量,是对近似熵的改进。样本熵表示非线性动力学系统产生新信息的概率,主要用来定量地刻画系统的规则度及复杂度。样本熵值越大,序列自我相似性越低,产生新信息的概率越高,序列越复杂[9]。可以用SampEn( m,r,N) 来表示样本熵,其中,N 为长度,r 为预先选定的相似容限,m 为预先选定的模式维数。样本熵的具体算法[10-11]如下:
设原始数据为x(1) ,x(2) ,…,x( N) ,共N 点。
1) 按序号连续顺序组成一组m 维矢量,从Xm(1) 到Xm( N - m +1) ,其中:

2) 定义X( i) 与X( j) 之间的距离d[Xm( i) ,Xm( j) ]为两者对应元素中差值最大的一个,即:
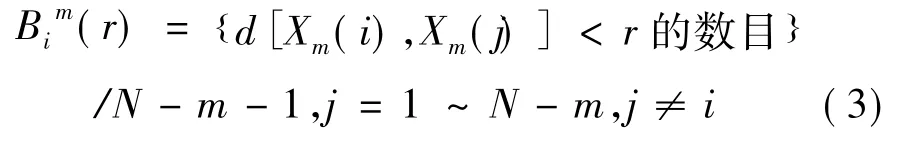
求其对所有i 的平均值,即:
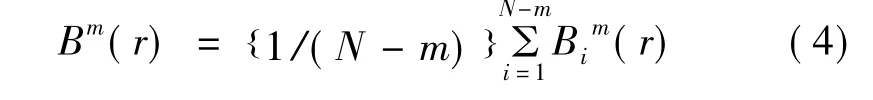
4) 将维数增加1,变为m+1 维矢量,重复式(1)~式(3) 的步骤后,得:

式中:Bm( r) 和Bm+1( r) 分别为m 点和m +1 点两序列相似的概率,则序列理论上的样本熵为:

当N 为有限时,得出序列样本熵估计值,即:

参数m、r 的选择是样本熵估计的关键,但目前为止没有最佳标准,根据以往研究[8~9,12],通常取m=2,r = 0.2SD,SD 为原始序列的标准差。利用Matlab R2009a软件进行编程计算。
1.2 研究区域
本文以阿城站为例,对其1961—2010年逐月实测径流序列进行复杂性分析。阿城站位于黑龙江省阿城市阿城镇,是松花江支流阿什河下游控制站,集水面积2 313 km2。阿什河属于半山区性河流,上游为山区,平均坡降1/500 左右,中游坡降为1/1 000 ~1/1 500,下游河道进入平原,坡降为1/1 500 ~1/1 800。此流域地处松花江中游,地形东南高、西北低,上游山峦起伏,生长着大片的次生林;中下游为丘陵平源,土壤肥沃,植被茂盛。本区属中寒温带大陆性季风气候区,春季回暖快,多风少雨,易发生春旱;夏季温热,暴雨集中,易发生洪水;秋季凉爽降温快,霜冻寒流来的早;冬季寒冷干燥。本站多年平均径流量为4.537 ×108m3;多年平均年降水量512.0 mm,主要集中在汛期6—9月份,占年降水量的82.0%。
2 结果与分析
2.1 径流序列样本熵的动态变化
为描述阿城站月径流序列复杂性的动态变化,以其1961—2010年的逐月实测径流时间序列为样本,以120个月的数据长度为滑动窗口,沿径流时间序列H( t) ( t=1,2,…,N) 移动,滑动步长为1,直至序列结束。对每个窗口内的数据计算其样本熵值,根据计算值绘制径流序列样本熵值的动态变化曲线,见图1。

3) 给定阈值r,对每一个1≤i≤N -m 值,统计d[Xm( i) ,Xm( j) ]<r 的数目( 模板匹配数) 及此数目与距离总数N-m-1 的比值,记作Bim( r) :

图1 阿城站月径流序列样本熵动态变化曲线
由图1 可知,在1961—2010年,阿城站月径流序列SampEn 值具有较为显著的周期性变化特征,开始呈现逐渐减小的趋势,然后呈现明显增加的趋势,造成这种发展趋势的可能原因有降水、下垫面条件、蒸发、气温、土壤蓄水状况等水文地质条件及人类活动如修建排水工程及河道护坡、修建水库及水闸等。同时可知,阿城站月径流序列复杂度具有明显的随时间变化而变化的特征,SampEn 值由最初的平稳波动状态转变是逐渐持续减小的总体发展态势,这说明在流域自然环境相对稳定的状态下,人类生产活动对水文系统的影响程度较大。
2.2 径流序列样本熵与径流量的关系
由图2 可知,阿城站月径流序列与其相对应的SampEn 值之间存在着某种相关关系。具体来说,在以120个月为滑动窗口的条件下,阿城站月径流量滑动平均值与其相对应的SampEn 值之间存在着负相关关系,而且在两者波峰处存在着非常明显的对应关系。若月径流量滑动平均值增加,则与其相对应的SampEn 值就会减小,说明径流在向有序方向发展,径流序列复杂性正在减弱;反之,若月径流量滑动平均值减小,则与其相对应的SampEn 值就会增大,说明径流在向无序方向发展,径流序列复杂性正在加强。

图2 阿城站月径流量与其样本熵关系曲线
3 结 论
本文运用样本熵方法分析了阿城站月径流序列的复杂性特征,初步得出以下结论:
1) 样本熵的动态分析结果表明,阿城站月径流序列的复杂性具有明显的时间差异,SampEn 值的波动较大且具有显著的周期性特征,这反映了不同时期的水利工程建设、护坡建设等人类生产活动对水文系统动力学结构产生了重大影响,从而导致了月径流序列复杂性的明显波动。
2) 阿城站月径流量滑动平均值与其相对应的SampEn 值之间存在着负相关关系,而且两者波峰处的对应关系非常明显,这种变化特征及对应关系对于当地径流序列的高精度预测研究具有重大意义。
3) 样本熵的计算不依赖数据长度,只需较少的数据就能反映时间序列的非线性特征,而且对缺失数据不敏感,算法方便易行,计算结果具有较高一致性,为径流序列及其它水文时间序列的复杂性研究提供了一种新的方法。
[1]冯国章,宋松柏,李佩成. 水文系统复杂性的统计测度[J]. 水利学报,1998(11) :76 -81.
[2]姜林,艾波,漆涛. 分形理论在软件复杂度中的应用[J].计算机应用,2010,30(10) :2730 -2734.
[3]刘函林,黄华,刘圹彬. 脑电信号分析的实用符号动力学方法研究[J]. 生物医学工程学杂志,2010,27(2):407-410.
[4]曹蕾,于国荣. 长江日流量时间序列混沌特性研究——相空间嵌入维数和嵌入滞时的联合确定[J]. 水利科技与经济,2011,17(7) :9 -11.
[5]童勤业,孔军,徐京华. 脑电复杂性分析的新方法[J]. 中国生物医学工程学报,1998,17(3) :222 -226.
[6]李素兰. 脑电时间序列分析的非线性动力学方法[D].杭州:浙江大学,1998.
[7]Richman J S,Moorman J R. Physiological time-series analysis using approximate entropy and sample entropy[J]. Am J Physiol Heart Circ Physiol,2000,278:H2039 -H2049.
[8]白冬梅,邱天爽,李小兵. 样本熵及在脑电癫痫检测中的应用[J]. 生物医学工程学杂志,2007,24(1) :200 -205.
[9]彭涛,陈晓宏,庄承彬. 基于样本熵的东江月径流序列复杂性分析[J]. 生态环境学报,2009,18(4) :1379 -1382.
[10]葛家怡,周鹏,赵欣. 睡眠脑电时间序列的非线性样本熵研究[J]. 电子器件,2008,31(3) :972 -975.
[11]Alcaraz R,Rieta J J.A review on sample entropy applications for the non -invasive analysis of atrial fibrillation electrocardiograms[J].Biomedical Signal Processing and Control,2010,5(1) :1 -14.
[12]苏文胜,王奉涛,朱泓等. 基于小波包样本熵的滚动轴承故障特征提取[J]. 振动、测试与诊断,2011,31( 2) :162 -166,263.

