二元泰勒展式在求解函数极限中的应用*

杨元超， 张守贵

(重庆师范大学 数学学院，重庆401331)

二元泰勒展式在求解函数极限中的应用*

杨元超， 张守贵

(重庆师范大学 数学学院，重庆401331)

利用二元函数的泰勒公式求解二元函数的极限，并用若干例题说明了该方法的运用.

二元泰勒展式；函数极限；应用

函数极限是高等数学中的一个基本概念，也是高等数学课程中的一个重要内容.常见的一些基本一元函数极限问题及求法有很多方法，如：利用极限的四则运算求函数极限，利用两个重要的极限求函数的极限，利用洛必达法则求函数的极限，利用迫敛性求函数极限，利用泰勒展式求函数极限等[1，2].而用多元函数的泰勒展式求多元函数极限方法，在已有文献中却少见这方面的报道.此处探讨了用二元函数的泰勒展式求二元函数极限的方法及其运用.

1 二元函数的极限[3]

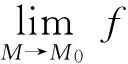
然而，用定义来求解二元函数的极限是比较麻烦的，下面探讨用二元函数的泰勒展式求解二元函数极限的方法.

2 二元函数的泰勒展式

定理1[4]设z=f(x，y)在点(x0，y0)的某一邻域内连续且有直到(n+1)阶连续偏导数，(x0+h，y0+k)为此邻域内任意点，则有：

(1)

其中，

(2)

式(1)称为二元函数f(x，y)在(x0，y0)的n阶泰勒公式，式(2)称为其拉格朗日型余项.

当n=0时，公式(1)成为：

f(x0+h，y0+k)=f(x0，y0)+hfx(x0+θh，y0+θk)+kfy(x0+θh，y0+θk)

(3)

称式(3)为二元函数的拉格朗日中值公式.

3 利用二元泰勒展式求二元函数极限

利用上述二元函数的泰勒展式求解了一些具体二元函数的极限，以此来说明此外提出的算法是有效的、可行的.

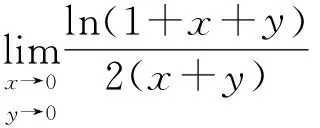
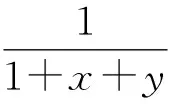
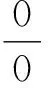
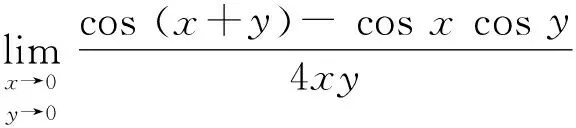
解先求函数f(x，y)=xy在点(1，1)的三阶泰勒展式[5].

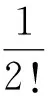
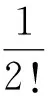
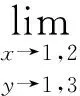
解将ex+y在(0，0)处展开得：

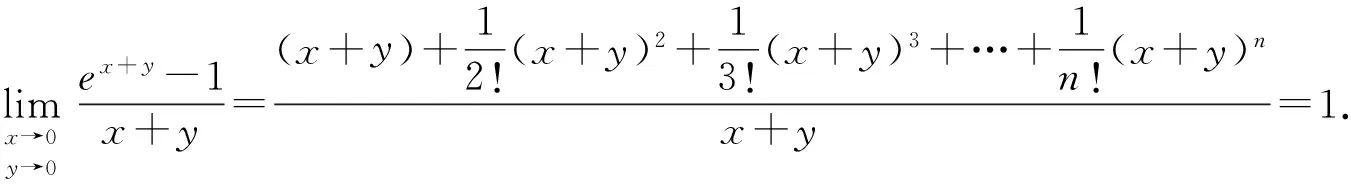
从上面的若干例题可以看出，应用一些二元函数泰勒公式求解某些二元函数的极限简单易行.

[1] 李国华.函数极限的几种求法[J].高师理科学刊,2011,31(3)：16-18

[2] 于吉亮,汪俭彬.函数极限的若干求解方法[J].天中学刊,2011,26(2)：79-80

[3] 陈传璋，金福林.数学分析(下)[M].北京：高等教育出版社,1983

[4] 同济大学应用数学系.高等数学下[M].5版.北京：高等教育出版社,2002

[5] 同济大学应用数学系，彭舟.高等数学同步辅导下[M].5版.北京：航空工业出版社,2004

[6] 黄辉,年福耿.二元函数极限计算方法探究[J].数学学习与研究,2012(17)：76

Keywords：bivariate Taylor expansion；function limit；application

Application of Bivariate Taylor Series Expansions to Solving Function Limit

YANGYuan-chao,ZHANGShou-gui

(School of Mathematics, Chongqing Normal University, Chongqing 401331, China)

This paper usesTaylor formula of bivariate function to solve the limit of bivariate function and uses several examples to illustrate the application of this method.

1672-058X(2013)10-0025-03

2013-04-16；

2013-05-10.

重庆师范大学科研项目(No.13XL001).

杨元超(1989-)，男，重庆潼南人，硕士研究生，从事数学课程与教学论研究.

O13

A

责任编辑：李翠薇