一夹一顶细长轴车削有限元数学建模*

聂 君

(重庆五一高级技工学校，重庆 400042)

一夹一顶细长轴车削有限元数学建模*

聂 君

(重庆五一高级技工学校，重庆 400042)

将加跟刀架采用一夹一顶装夹的细长轴车削系统处理成三单元四节点有限元离散模型，利用空间梁单元建立细长轴的整体刚度矩阵，再结合切削力模型、跟刀架力学模型和工件变形位移模型建立细长轴的节点平衡方程。该方程同时考虑了实际切削力和工件变形间的耦合关系，能对细长轴切削点的变形位移进行较高精度求解。

细长轴车削；有限元；耦合；变形位移

通常把长径比大于25的轴类零件称为细长轴。细长轴车削由于刚性差，在切削力作用下容易产生弯曲变形和振动，因此一直被归为复杂零件加工。关于细长轴车削的研究，现阶段不少学者都是借助ANSYS这类CAE软件进行仿真分析，而较少直接建立数学模型展开讨论。细长轴车削时因工件受力产生弯曲变形而改变刀具的实际背吃刀量，进而改变实际切削力大小，实际切削力反过来又会影响工件的实际变形位移，由此不难看出车削中实际切削力与工件弯曲变形间存在耦合效应。利用ANSYS软件编写命令流对以上耦合关系进行求解存在一定难度，因此针对加跟刀架采用一夹一顶的细长轴车削(图1)，尝试利用有限元法建立细长轴的节点平衡方程来求解切削点的实际变形位移。

图1 细长轴一夹一顶车削

图2 空间梁单元的节点力

1 空间梁单元矩阵

考虑到细长轴具有直梁特征，因此在建立细长轴车削离散模型时，选用空间梁单元进行建模，如图2所示。根据文献[1]对空间梁单元的推导，结合细长轴大长径比的特点，得到12×12阶的梁单元刚度矩阵：

E为材料弹性模量，I为细长轴截面惯性矩，G为材料剪切模量，A为细长轴截面面积，Ip为细长轴截面极惯性矩，le为单元长度。

2 跟刀架模型及其他边界条件的确定

如图3所示，建模时可将跟刀架的两个支承爪考虑成与X和Y轴平行的受压弹簧[2]，其刚度分别为kx和ky。

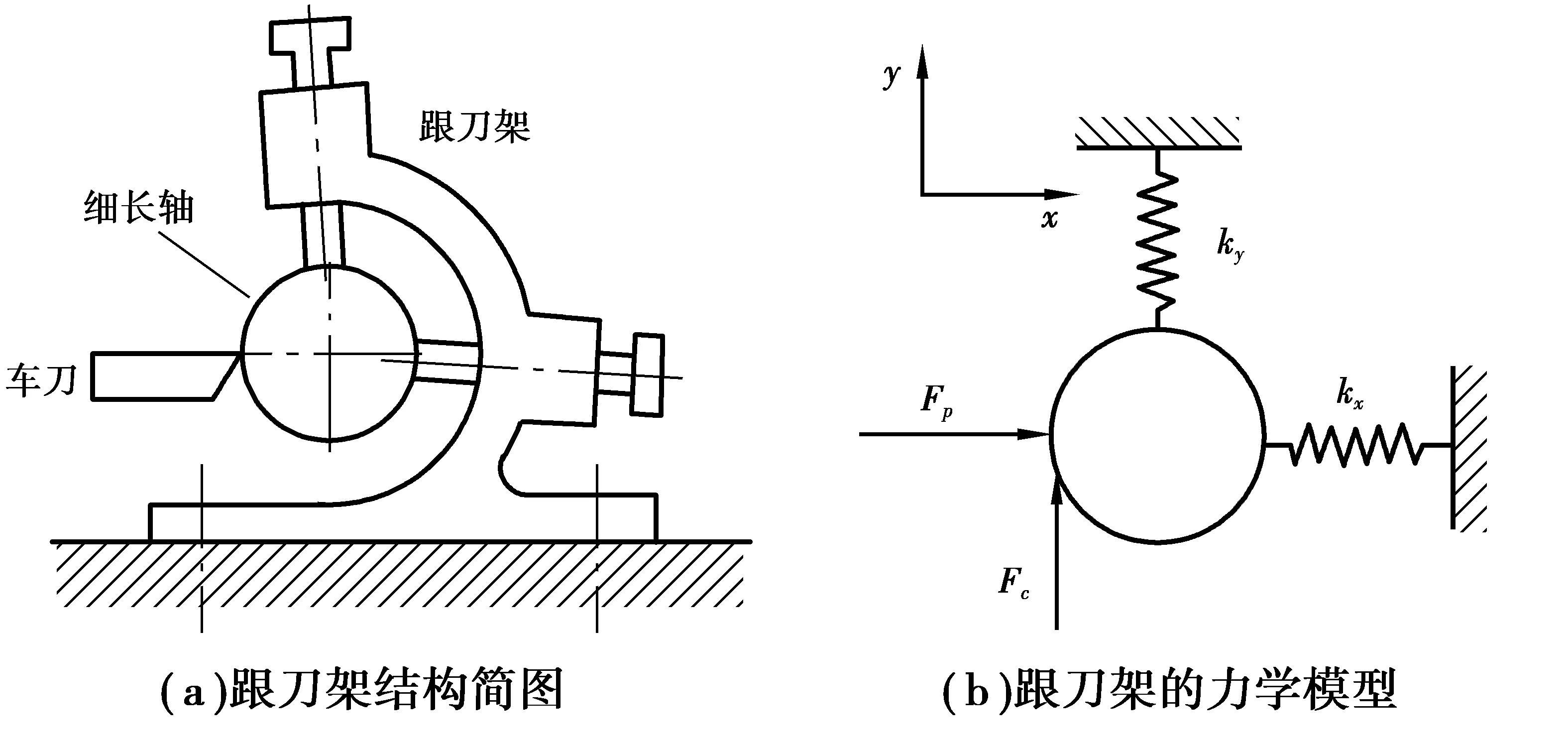
图3 跟刀架及其力学模型

针对一夹一顶装夹，可将卡盘端视为固定端约束，顶尖端视为移动铰支座约束，得到细长轴车削系统的3单元4节点离散模型，如图4所示：

图4 细长轴车削系统的离散模型

图4从左到右的4个节点分别为卡盘的夹持点、切削点、跟刀架接触点以及顶尖的支承点。节点1、2之间的部分为单元①，节点2、3之间为单元②，节点3、4之间为单元③。利用直接刚度法将3个单元刚度矩阵组合成细长轴车削系统的整体刚度矩阵：

细长轴的节点平衡方程则可表示为：

[K]·[δ]=[F]

(1)

式中，[K]—细长轴整体刚度矩阵，[F]—节点力矩阵，[δ]—节点位移矩阵

3 边界条件处理

3.1 位移条件

考虑节点1为固定端，有U1z=U1x=U1y=φ1z=φ1x=φ1y=0；节点4为简支端，有U4x=U4y=0。将以上位移向量在节点平衡方程中对应的行列删除，方程化简得：

3.2 载荷条件

① 切削力。细长轴车削时在节点2处分别受X、Y和Z向的切削分力作用，根据经验切削力公式[3]，空间切削分力表达式如下：

主切削力：

(2)

背向力：

(3)

进给力：

(4)

以上各项系数、指数及修正系数均可根据车削刀具的几何角度和切削用量查阅相关手册得到。

② 际背吃刀量。车削过程中，刀具和工件受切削力作用会产生弯曲变形(即让刀现象)，该变形量会影响车削时的实际背吃刀量，从而改变实际切削力大小，实际切削力的改变反过来又会影响工件的弯曲变形程度，因此实际切削力与工件变形位移间存在耦合效应。

图5 细长轴车削时的工件偏移模型

切削力大小与工件变形位移的联系主要体现在背吃刀量上。背吃刀量分为名义背吃刀量ap和实际背吃刀量ape。加工中由于刀具和工件产生的让刀现象，使得实际背吃刀量ape通常会略小于名义背吃刀量ap。

在计算实际背吃刀量时，因细长轴自身径向刚度低，加工时主要由细长轴工件产生弯曲变形，故可以忽略刀具的变形位移，只考虑工件在水平X和竖直Y向上的偏移量[4]，如图5所示：

图中大圆dw表示工件的毛坯直径，双点划线dm表示车削后不考虑变形位移的工件名义直径和位置，小圆de表示车削后工件的实际直径和位置。由图可得：

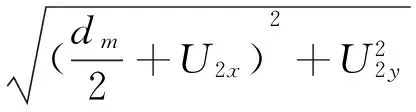
(5)

式中U2x，U2y——工件切削点在X和Y轴上的偏移量。

实际背吃刀量ape可表示为：

(6)

将该实际背吃刀量公式代入经验切削力公式，即可得到切削力与工件变形位移的函数关系。

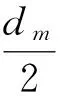
(7)

④ 跟刀架的接触力。根据跟刀架力学模型，节点3处的水平和竖直支承爪可视为与X、Y轴平行的弹簧，其接触力大小与接触点的偏移量成正比，可表示为：

F3x=-kxU3x，F3y=-kyU3y

(8)

综合以上载荷条件，得到载荷向量：

4 算例计算

设细长轴工件长度l=1 500 mm、毛坯直径dw=φ20 mm、截面面积A=314 mm2、截面惯性矩I=0.785 mm4、极惯性矩IP=15 700 mm4，工件材料为45钢，其弹性模量E=2.07×108N/mm2、剪切模量G=80×106N/mm2。跟刀架安装位置距离切削点l2=20 mm，支承爪材质为球墨铸铁，通过试验测得其X和Y向刚度分别为kx=4.47×103N/mm和ky=2.03×104N/mm。车削刀具选用YT15硬质合金车刀，其强度极限σb=600 MPa、屈服极限σs=355 MPa。具体刀具几何角度和切削用量如表1所示。试计算当车削至l1=860 mm时，细长轴在切削点处产生的变形位移U2x和U2y值。

表1 细长轴车削所选刀具几何角度及切削用量

将以上加工条件代入之前各式，建立细长轴节点平衡方程。由于细长轴刚度矩阵具有带状、对称、稀疏等特点，矩阵中大部分元素为零，因此可借助Matlab软件利用消元法编程求解，得到细长轴在切削点处的变形位移如表2所示：

表2 细长轴在切削点处的变形位移(mm)

相同工况，通过ANSYS软件作静力分析，所得结果如表3所示：

表3 ANSYS仿真结果(mm)

比较两组数据不难看出结果非常接近，验证了模型的准确性。利用ANSYS建模时通常是以给定切削力恒定值进行仿真模拟，因此相比而言，表2中的数据准确度更高。

5 结 语

将切削力模型、跟刀架力学模型和工件变形位移模型代入细长轴车削系统的节点平衡方程中，借此表达实际切削力与工件变形位移间的耦合关系，并尝试借助Matlab软件对特定工况下的细长轴在切削点处的变形位移进行了求解，求解结果与ANSYS仿真结果接近，验证了模型的准确性，为对细长轴车削作进一步的深入研究提供了依据。

[1] 朱伯芳. 有限单元法原理与应用[M]. 北京：中国水利水电出版社，2009

[2] 韩荣第，郭建亮. 加跟刀架的细长轴车削加工尺寸误差的仿真[J]. 南京航空航天大学学报，2005(11)：108-112

[3] 韩荣第，周明，孙玉洁. 金属切削原理与刀具[M]. 哈尔滨：哈尔滨工业大学出版社，2004

[4] PHAN A V，BARON L，MAYER J. Finite element and experimental studies of diameter errors in cantilever bar turning[J]. Applied Mathematical Modeling, 2003(27)：221-232

Keywords：slender shaft turning；finite element；coupling；deformation displacement

Mathematical Modeling with Finite Element for the Slender Shaft Turning with a Clamping Chuck and a Back Center

NIEJun

(Chongqing Wuyi Senior Vocational School, Chongqing 400042, China)

The follower rest is processed into 3-unit-4-node finite element discrete model by system of slender shaft turning with a clamping chuck and a back center, the whole stiffness matrix of slender shaft is set up through space beam element, slender shaft node balance equation is established by the combination of cutting force model, follower rest mechanical model and workpiece deformation displacement model and this equation simultaneously considers the coupling relation between real cutting force and workpiece deformation and can solve, in higher precision, the deformation displacement of the cutting point of the slender shaft.

1672-058X(2013)10-0034-07

2013-04-04；

2013-04-16.

聂君(1982-)，男，重庆市人，讲师，从事数控应用研究.

TG501

A

责任编辑：李翠薇