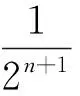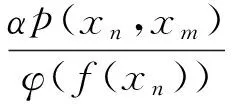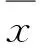带有q 距离的广义Ekeland变分原理的应用*
陈 娇
(重庆师范大学 数学学院,重庆 401331)
带有q距离的广义Ekeland变分原理的应用*
陈 娇
(重庆师范大学 数学学院,重庆 401331)
研究了广义Ekeland变分原理在分离赋范空间中的一些重要应用.利用广义Ekeland变分原理证明了函数f满足关于∂的Takahashiε-条件当且仅当f满足关于相同的∂的Hamelε-条件.
Ekeland变分原理;q距离;Takahashi-ε条件;Hemal-ε条件
基于Ekeland变分原理在非线性分析、优化控制论、动力系统等各方面都有广泛应用,许多作者从不同的角度进行了推广[1-9].特别地,Z.L.Wu[3]在完备度量空间中利用Ekeland变分原理证明了Takahashi-ε条件的等价定理,以及在弱尖极小及不动点等中的应用.J.H.Qiu[9]在分离赋范空间上建立了具有q距离的广义Ekeland变分原理,并利用其推导出广义Caristi不动点定理、广义Takahashi非凸最小化定理, 并证明其等价性等相关给论.
此处在分离赋范空间下引入q距离分别建立Takahashi-ε条件及Hemal-ε条件, 并利用广义Ekeland变分原理证明其等价性及一些相关结论.
1 预备知识
为了得到主要结果,首先引进下面的定义和引理.
定义1[9]设X是一个分离赋范空间,映射P:X×X→[0,+∞)满足:
(p1) ∀x,y,z∈X,p(x,z)≤p(x,y)+p(y,z).
(p2) 对任意序列{yn}∈X,满足p(yn,ym)→0(m>n→∞)是一个柯西列,p(yn,y)→0与yn→y等价.
(p3) 对每个x,y,z∈X,p(z,x)=0且p(z,y)=0,则x=y.
则称p是p距离.如果条件(p2)用下面更弱的条件:
(q2) 对任意序列{yn}∈X,满足p(yn,ym)→0(m>n→∞)是柯西列,p(yn,y)→0蕴含了yn→y.
则称p是q距离.
定义2 设(X,μ)是赋范空间,p是q距离.称真函数f:X→(-∞,+∞]关于p序列下单调的,如果对任意序列{xn}满足
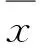
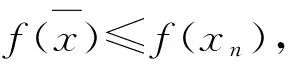
定义3 设(X,μ)是分离赋范空间P:X×X→[0,+)为q距离,φ:(-∞,+∞]→(0,+∞)为非减函数.f:X→R∪{+}为序列下单调、下有界的真函数.称f满足关于∂的Takahashiε-条件,如果存在ε,α,x∈X分别满足0<ε≤+∞,∂>0,infXf 称f满足关于相同的∂的Hamelε-条件,如果存在ε,α,x∈X分别满足0<ε≤+∞,∂>0,infXf 定理1 设(X,U)是分离赋范空间P:X×X→[0,+)为q距离,f:X→R∪{+}为关于p序列下单调,下有界的真函数.设(X,U)是关于(p,f)是序完备的,φ:(-,+]→(0,+)为非减函数.假设f满足下列条件: (A1) 对任意u∈X,f(u)>infx∈Xf(x),存在v∈X,v≠u,满足 定理2 设(X,U)是分离赋范空间P:X×X→[0,+)为q距离,φ:(-,+]→(0,+)为非减函数.f:X→R∪{+}为序列下单调、下有界的真函数.设(X,U)是关于(p,f)是序完备的,则对任意0<ε≤+,∂>0,f满足关于∂的Takahashiε-条件当且仅当f满足关于相同的∂的Hamelε-条件. 证明″⟹″对任意u∈X,设 则对任意的0<ε<+,只需证明对任意满足infXf 即x∈S∂(u). 下面证明z∩S∂(x)≠∅. 由前面的证明方法,有f(xn+1)≤f(xn).显然{f(xn)}是一个不减的下有界的实数列. 当n>m时,有xm∈S(xm-1)⊂S(xn),即 αp(xn,xm)≤φ(f(xn))(f(xn)-f(xm))≤φ(f(xn))(f(xn)-β)≤φ(f(x0)(f(xn)-β)→0,n→ 设m→,有则⊂S(xn),∀n=0,1,2,…. 注1 当X为完备度量空间,p(x,y)=d(x,y),φ(x)=1,f为有下界的真下半连续函数时, 定理2退化为文献[3]中的定理2.2. [1] ZHANG S S, CHEN Y Q,GUO J L. Ekeland’s variational principle and Caristi’s-xed point theorem in probabilistic metric space[J]. Acta Mathemeticae Applicatae Sinica, 1991,7(3):217-228 [2] LI Y X,SHI Z S. A Generalization of Ekeland’s2-Variational Principle and Its Borwein-Preiss Smooth Variant[J]. Journal of Mathematical Analysis and Applications, 2000,246:308-319 [3] WU Z L. Equivalent formulations of Ekeland’s variational principle[J]. Nonlinear Analysis, 2003(55):609-615 [4] BIANCHI M, KASSAY G, PINI R. Existence of equilibria via Ekeland’s principle[J]. Journal of Mathematical Analysis and Applications, 2005(305):502-512 [5] LIN L J, DU W S. Ekeland’s variational principle, minimax theorems and existence of noncon-vex equilibria in complete metric spaces[J]. Journal of Mathematical Analysis and Applications,2006(323):360-370 [6] LIN L J, DU W S. Some equivalent formulations of the generalized Ekeland’s variational principle and their applications[J]. Nonlinear Analysis, 2007(67):187-199 [7] Al-HOMIDAN S, ANSARI Q H, YAO J C. Some generalizations of Ekeland-type variational principle with applications to equilibrium problems and-xed point theory[J]. Nonlinear Analysis, 2008(69):126-139 [8] XIANG S W, YIN W S, WANG C C. Some new results on stability of Ekeland’s εvariational principle[J]. Journal of Mathematical Analysis and Applications, 2008(339):802-810 [9] QIU J H, FEI H. P-Distances,Q-Distances and a Generalized Ekeland’s Variational Principle in Uniform Spaces[J].Acta Mathematics sinica English Senies,2012(2):235-254 [10] EKELAND I.Sur les probemes variationnels[J].Comptes Rendus de l’Académie des Sciences-Series I, 1972(275):1057-1059 [11] EKELAND I. On the variational principle[J]. Journal of Mathematical Analysis and Application,1974(47):324-353 [12] CHEN Y Q, CHO Y J, YANG L. Note on the results with lower semi-continuity[J]. Bulletin of the Korean Mathematical Society, 2002,39(4):535-541 Keywords:Ekeland variational principle;q distance;ε-condition of Takahashi;ε-condition of Hamel Application of Generalized Ekeland Variational Principle with q Distance CHENJiao (School of Mathematics, Chongqing Normal University, Chongqing 401331, China) Some important applications of generalized Ekeland variational principle to separated normed space are studied, the generalized Ekeland variational principle is used to prove that function f satisfiesε-condition of Takahashi with ∂ if and only if f satisfiesε-condition of Hamel with the same ∂. 1672-058X(2013)10-0001-04 2013-04-08; 2013-05-25. 国家自然科学基金项目(10831009);重庆自然科学基金项目(2011BA0030);重庆市科委运筹学与系统工程重庆实验室专项经费资助(CSTC,2011KLORSE02);重庆市教委科技项目资助(KJ110625). 陈娇(1988-),女,重庆铜梁人,硕士研究生,从事变分分析及应用研究. O176;O177.91 A 责任编辑:李翠薇

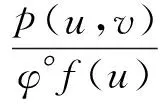
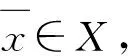


2 主要结果