分块矩阵的加权Moore-Penrose逆*

杨晓英, 刘 新

(四川信息职业技术学院 基础教育部, 四川 广元 628017)

分块矩阵的加权Moore-Penrose逆*

杨晓英, 刘 新

(四川信息职业技术学院 基础教育部, 四川 广元 628017)

给出分块矩阵关于子块在加权M-P逆意义下的广义Schur补的加权M-P逆的表示和分块矩阵加权M-P逆表示的一个充要条件.

分块矩阵；广义Schur补；加权M-P逆；正定矩阵

1 概 述

设Cm×n是m×n阶复矩阵的集合,Crm×n是秩为r的m×n阶复矩阵的集合,A*表示矩阵A的共轭转置，A+表示矩阵A的M-P逆.

加权广义逆问题已经引起许多学者的注意，它可应用于数值计算，统计学，控制系统与分析和鞍点问题等.近年来，许多学者对加权Moore-Penrose逆的表示做了研究[1-4].2006年,张燕等学者给出矩阵加权Moore-Penrose逆存在的一些充分必要条件[2]； 2009年, 国欣荣等得到环上矩阵存在关于M,N加权Moore-Penrose逆的一个充要条件[3]； 2010年, 刘声等给出块对角矩阵的加权广义逆的表达式[4]； 周立仁利用奇异值分解，给出了矩阵15种加权Penrose型广义逆的通式与表达式[5]； 章里程等利用加权Moore-Penrose逆的定义和性质， 获得了2×2、1×2和2×1分块矩阵关于加权Moore-Penrose逆块独立的一些充分必要条件[6,7]； 2012年, 何兴月等用环论的方法, 得到Qu{mtale上矩阵存在加权M-P广义逆的一些等价刻画及显式表达式[8].主要用定义验证的方法，给出分块矩阵的加权M-P逆表示的充要条件，并给出广义Schur补与加权M-P逆子块的几个关系式.

首先介绍一些基本的定义.

定义1[9]设A∈Cm×n,M∈Cm×m,N∈Cn×n是Hermite正定矩阵, 如果存在唯一矩阵X∈Cm×n, 满足下列4个方程：

下面给出广义Schur补的定义, 以备后面加权广义逆表示之用.

设矩阵H∈C(m+p)×(n+q), 分块为：

(1)

其中A∈Cm×n,B∈Cm×q,C∈Cp×n,D∈Cp×q

2 主要结果

下面首先给出分块矩阵H关于A和D在加权M-P逆意义下的广义Schur补的表示.

定理2.1 若H具有形如(1)的分块形式，M1和M2分别是m×m和p×p阶的正定矩阵，N1和N1分别是n×n和q×q阶的正定矩阵，且满足：

那么

证明： 由矩阵加权M-P逆的定义容易验证.

下面给出分块矩阵加权M-P逆表示的一个充要条件.

(2)

当且仅当

(3)

当且仅当

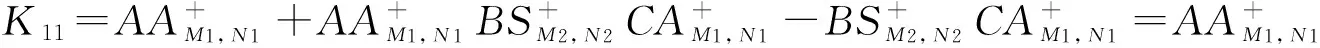
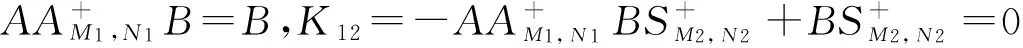
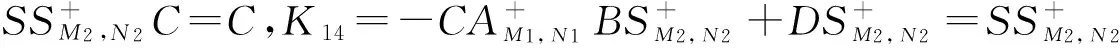
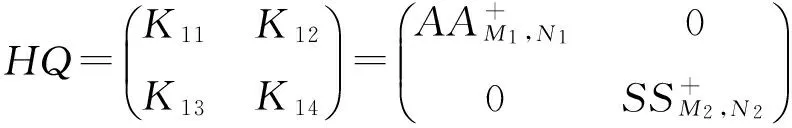
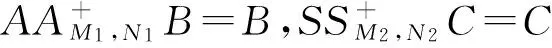
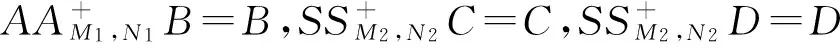
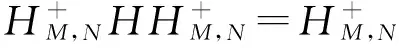
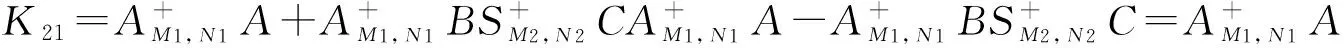
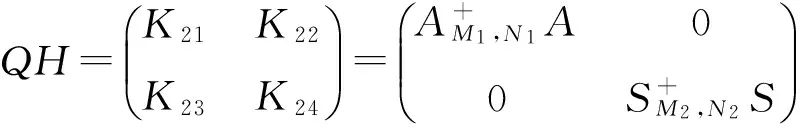
其中

即：

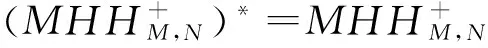
其中

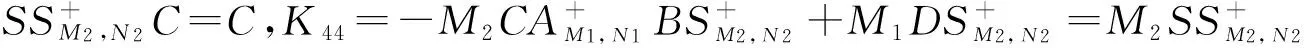
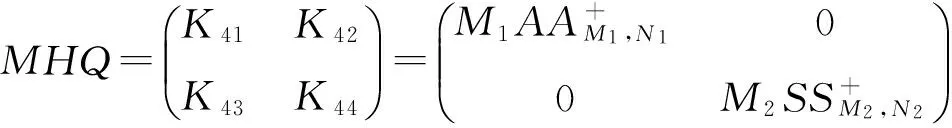
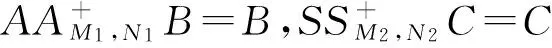
所以

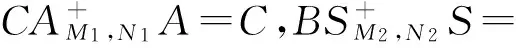
所以

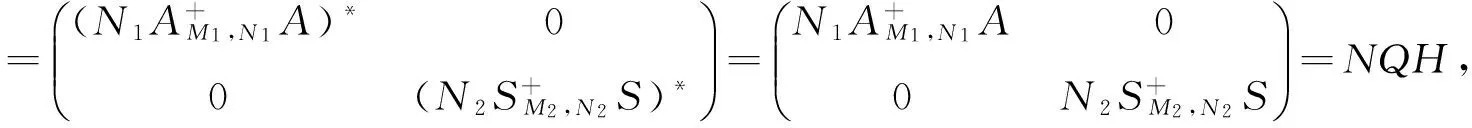
结合4个等式成立的充要条件是

故式(2)成立.

用同样的方法可以证明式(3)成立.

3 结 论

首先给出广义Schur补的表示,然后根据加权M-P逆需满足的4个等式给出分块矩阵加权M-P逆表示的一个充要条件.

[1] DRAGANA S, CVETKOVI I. Expression of the Drazin and MP-inverse of partitioned matrix and quotient identity of generalized Schur complement[J].Applied Mathematics and Computation,2009,213：18-24

[2] 张燕,郭鹏江,鲁静华.关于一般矩阵的加权Moore-Penrose逆[J].西南科技大学学报,2006,2l(1)：91-94

[3] 国欣荣,岑建苗.环上矩阵加权Moore-Penrose 逆存在的条件[J].宁波大学学报：理工版,2009,22(3)： 383-386[4] 刘声,何淦瞳.分块对角矩阵的加权广义逆[J].贵州大学学报：自然科学版,2010,27(4)：19-21

[5] 周立仁.矩阵加权Moore-Penrose 逆的通式[J].青海师范大学学报：自然科学版,2010,2：1-6

[6] 郭华.全转置正交矩阵[J].重庆工商大学学报：自然科学版,2013,30(1)：18-20

[7] 章里程,廖祖华.分块矩阵加权Moore-Penrose逆的块独立性[J].数学杂志,2010,30(5)：921-925

[8] 何兴月,廖祖华,胡淼涵,等.Quantale矩阵的加权M-P广义逆[J].四川师范大学学报：自然科学版，2012,35(3)：340-344

[9] 程云鹏,张凯院,徐仲.矩阵论[M].西安：西北工业大学出版社,2007

[10] 周立新.分块广义幂等矩阵的广义Schur补的一些性质[J].贺州学院学报,2011,27(2)：129-131

Keywords：block matrix；generalized Schur complement；weighted M-P inverse；positive definite matrix

Weighted Moore-Penrose Inverse of Block Matrix

YANGXiao-ying,LIUXin

(Department of Basic Education,Sichuan Information Vocational College, Sichuan Guangyuan 628017, China)

This paper gives weighted M-P inverse representation of generalized Schur complement under the meaning of weighted M-P inverse about the block of block matrix and presents a sufficient condition for the representation of weighted M-P inverse of block matrix.

1672-058X(2013)10-0013-04

2013-03-17；

2013-04-25.

四川信息职业技术学院自然科学基金(2012C04).

杨晓英(1984-)，女，山西祈州人，讲师，硕士，从事矩阵理论与应用研究.

O151.21

A

责任编辑：田静