输运方程数值解法分析

王海林，魏丙涛，刘天祥，桂朝觐，高全归

（1.玉溪师范学院 理学院，云南 玉溪 653100；2.文山学院 数理系，云南 文山 663000）

输运方程是数学物理方程中的一类最基本的方程，在许多情况下，由于边界条件比较复杂，或者由于方程比较复杂，或由于其他各种原因，难以严格解出［1］。因此，近似解法得以发展，只要近似程度能够满足实际需要，近似解的价值并不低于严格解，随着电子计算机的日渐普及，用数值方法求解方程的近似解变得非常方便。

数值解法求解偏微分方程的方法有多种，应用比较普遍的有有限差分法，变分法和有限元方法，有限差分法一般应用于求解含时间问题比较方便。解同样的离散微分方程，采用好的算法与采用一般的算法的计算效果往往相差很大，采用好的算法不但能使求解过程数值稳定、数值解的精度得到提高，而且能数十倍、数百倍地节省计算工作量［2］。本文将通过不同的数值算法求解相同的定解问题，给出数值方法求解输运方程的一些有趣的结果。

1 定解问题

在数学物理方程中，输运方程有很多，比如扩散方程、热传导方程等。在此，用一个比较简单的方程，来考察差分格式对数值结果的影响，以下面的定解问题为例：

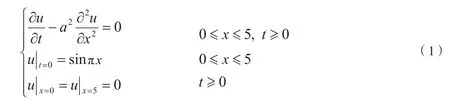
当然上述定解问题可以用分离变量的方法求得其解析解为：

于是可以给出解析解的函数图像，这里给出函数值u随x和t变化的函数关系图（见图1）：

从图1中可以看出，随着时间的增加，函数值逐渐衰减，函数值随空间坐标按正弦规律变化，这与定解问题给出的解析解是一致的，需要说明的是在得到解析解的过程中已经考虑了初始条件和边界条件。

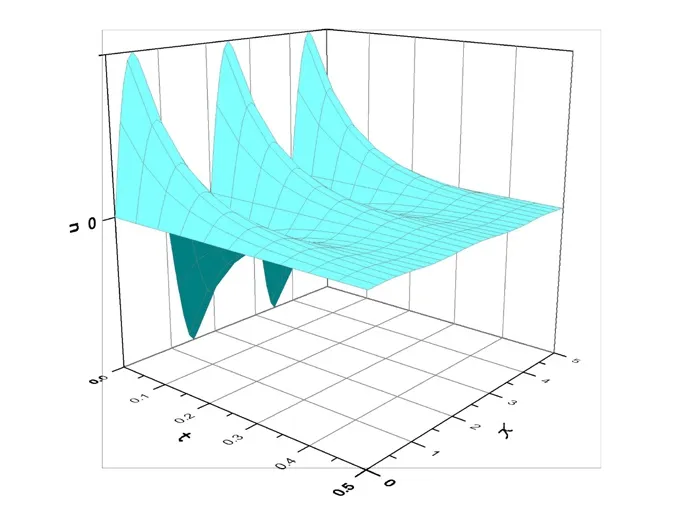
图1 函数值u随x和t变化的解析解的函数图像

2 数值方法

2.1 方程及初边界条件的离散化

对上述方程的离散化方法有很多，在此对方程采用两种离散方法：向前差分和向后差分，离散后向前差分格式的方程可以写为［3］：

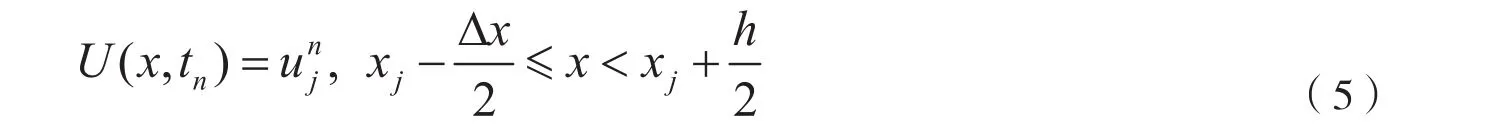
这里使用U（x，tn）仅仅是为了和微分方程中的函数值u相区分，于是（4）式可以改写为

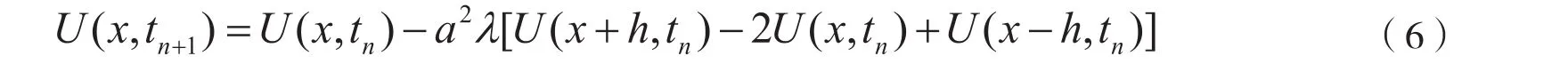
对（6）式等式左右两边同时做傅里叶积分可得：

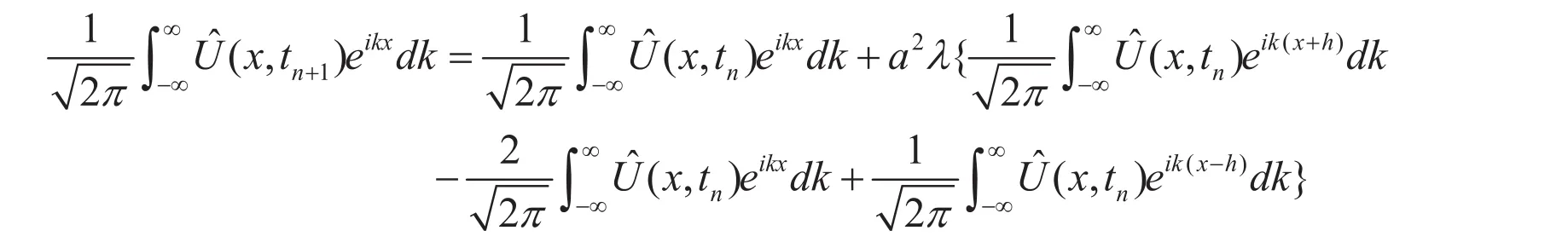
上式可以化简为：

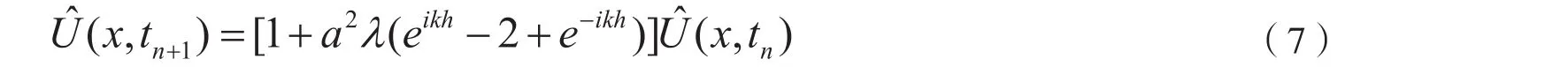
离散后的向后差分格式的方程可以写为［5］：

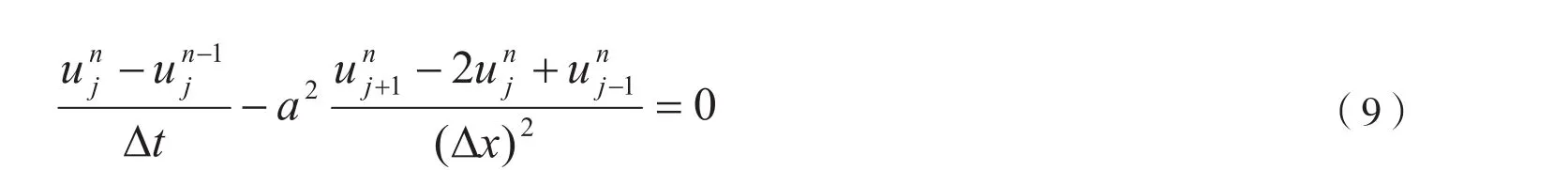
这个差分格式是一个绝对稳定的格式，虽然这样的差分格式的截断误差也为，但是，这样的离散在实际的计算中会存在比较大的误差。

由于定解问题中的边界全为0，这样边界条件很好处理，在边界处直接取0，但初始条件需要离散化，初始条件取为：

有了上面的离散化后就可以进行数值求解了。数值求解的过程中使用Visual C++6.0作为编译器，图形用Origin8.5画出。

2.2 不同差分格式对结果的影响

图2和图3分别运用向前差分的方法计算了t=0.5时的定解问题的解，图2的求解中取a2λ=0.5，刚好能满足稳定性条件，图3不满足稳定性条件，在图3中取a2λ=1。可见，计算过程中不满足稳定性条件a2λ≤0.5时，数值解法是不稳定的，不稳定的解没有意义。表1中给出了向前差分格式对应的不同网格比得到的数值解。由表1中可以看出，当a2λ=1时，函数值得振荡特别严重，这是不稳定的表现。

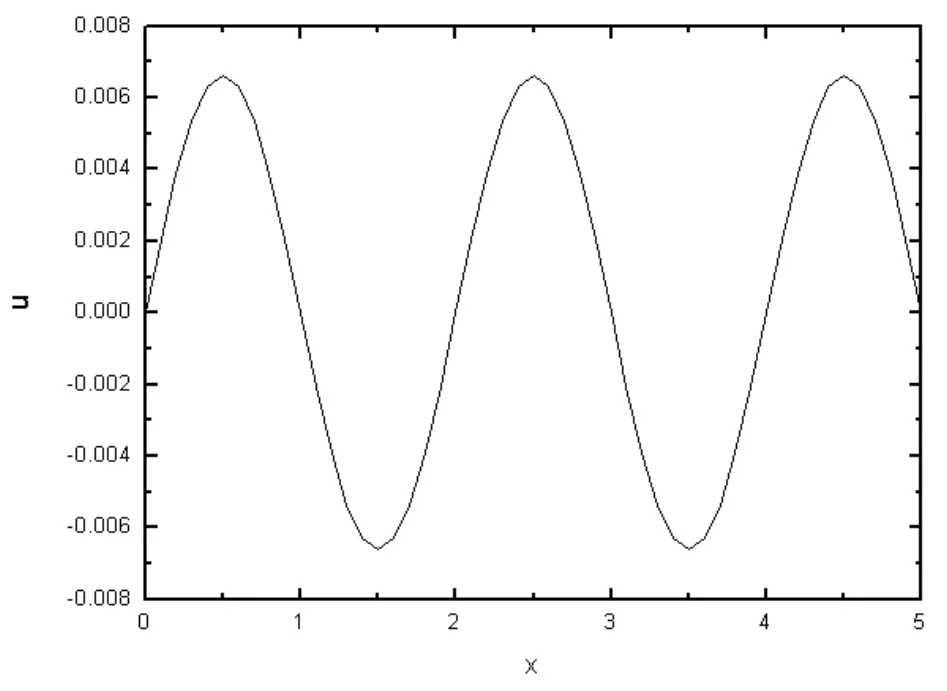
图2 t=0.5时网格比为1/2时的函数图

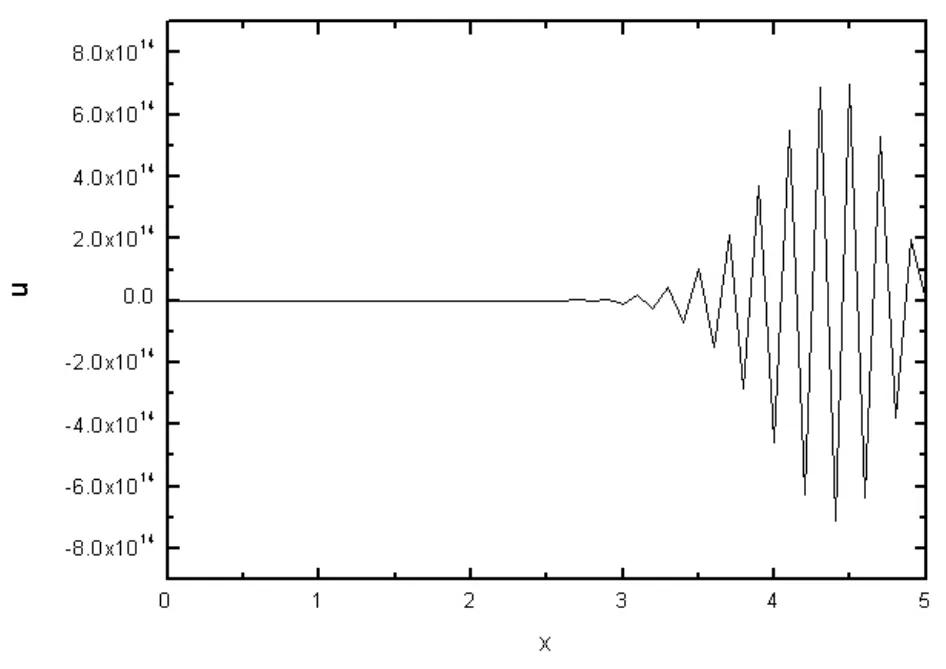
图3 t=0.5时网格比大于1/2时的函数图

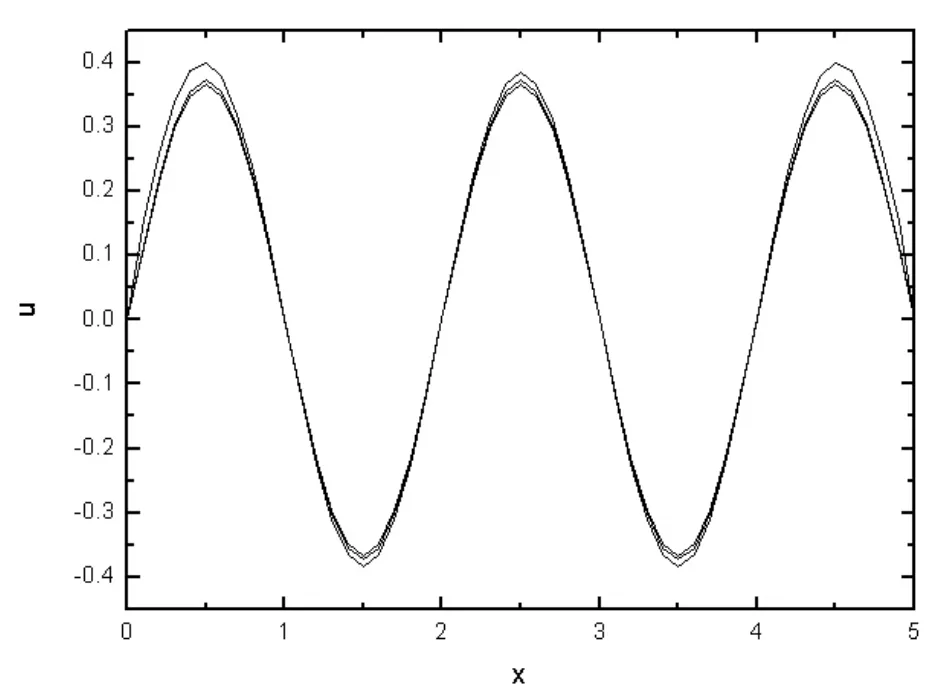
图4 t=0.1时解析解和两种差分结果的比较

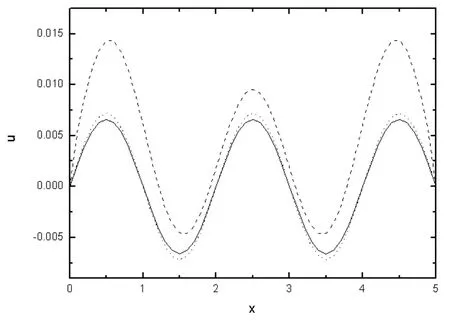
图5 t=0.5时解析解和两种差分结果的比较

图4给出了t=0.1时解析解和两种数值解法的比较，由图4可以看出，三种解法的误差很小，而向前差分和解析解的结果更加接近。图五给出了t=0.5时解析解与两种差分格式的数值解的比较，其中点线为解析解的结果，实线为向前差分格式的数值结果，虚线为向后差分的数值结果。有趣的是向后差分格式虽然在任何情况下都是稳定的，但是，误差比较大，随着数值计算中不断的迭代，误差越来越大，而向前差分只要满足稳定性条件，误差比向后差分要小的多。这是容易理解的，因为在数值计算中，向前差分是由前一个时间层上的三个点来计算下一个时间层上一个点的值，而向后差分是在两个时间层上建立线性方程组来求解，因而，其误差更大。表2中分别给出了解析解、向前差分格式和向后差分格式在t=0.1时及t=0.5时的数值结果，从表2中的数值解的结果可以看出当t=0.1时数值解的误差较小，但当t=0.5时向后差分的误差就变大了。需要指出的是解析解用数值形式表出的时候依然是存在误差的，主要是由于π的取值是存在误差，但这个误差很小，在很多实际应用中时可以忽略的。

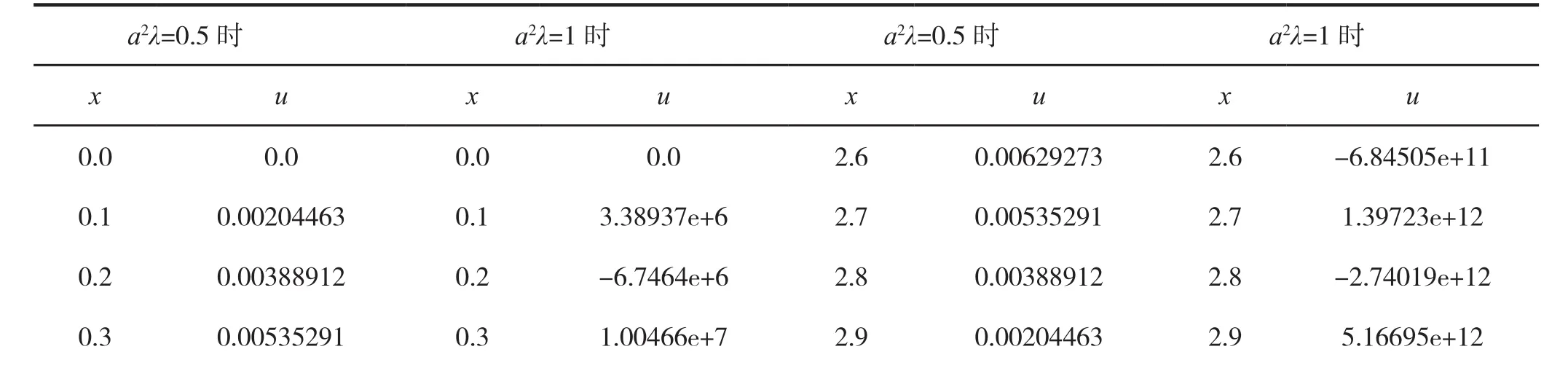
表1 向前差分格式对应不同的网格比得到的数值解

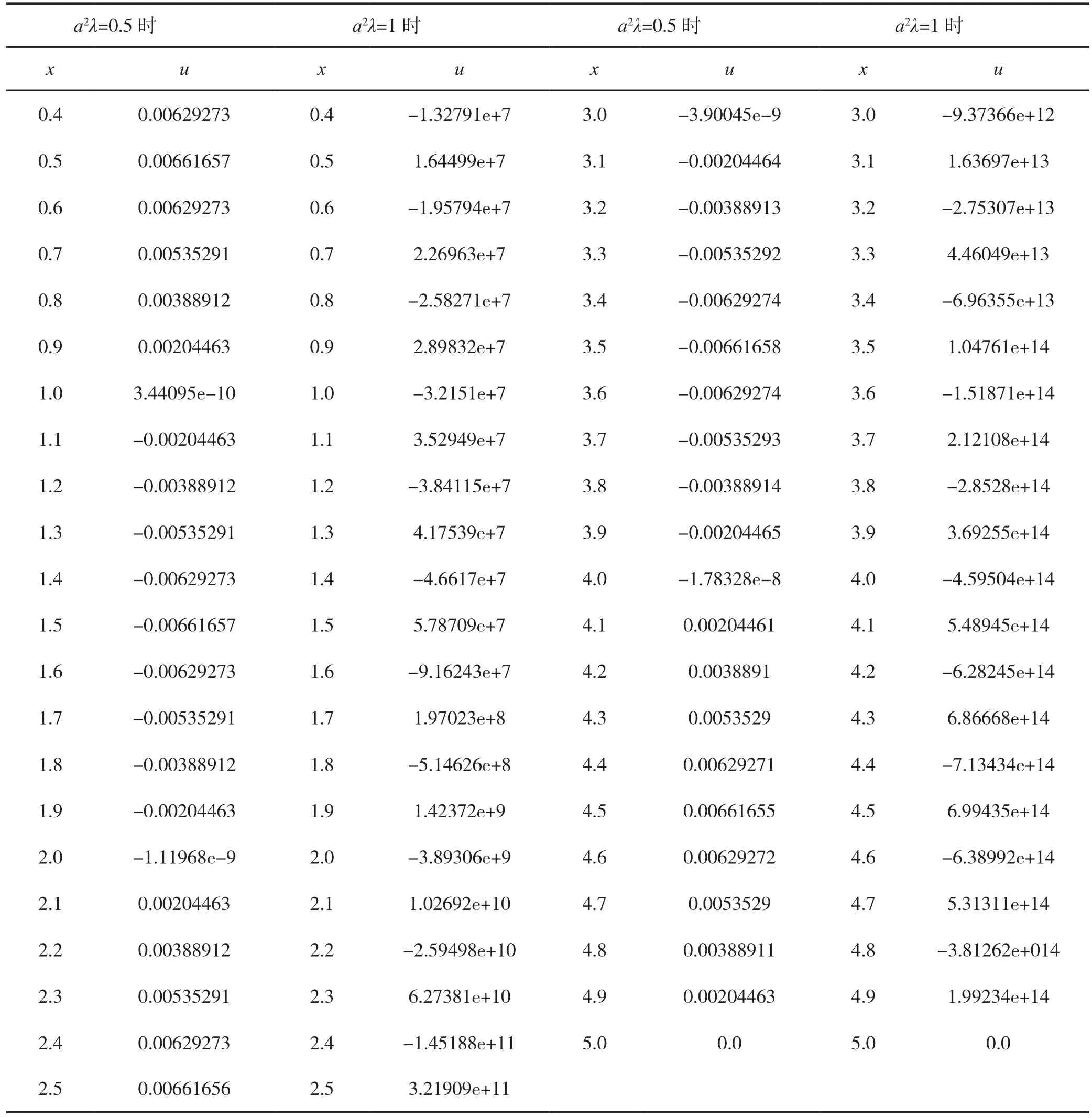
（续表1）

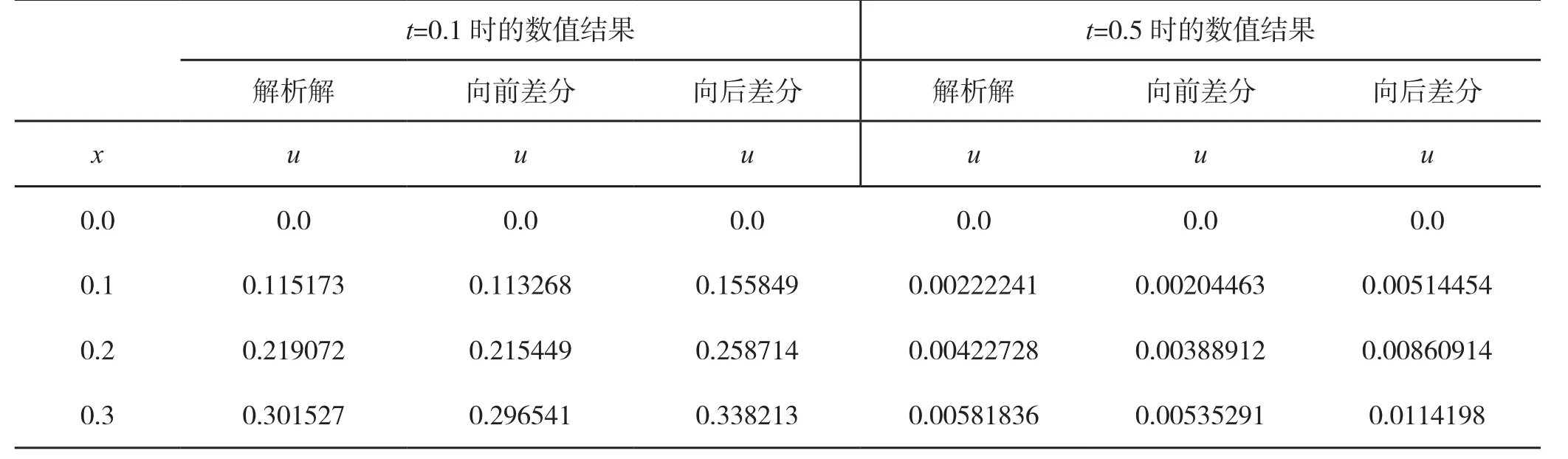
表2 解析解、向前差分格式和向后差分格式在t=0.1时及t=0.5时的数值

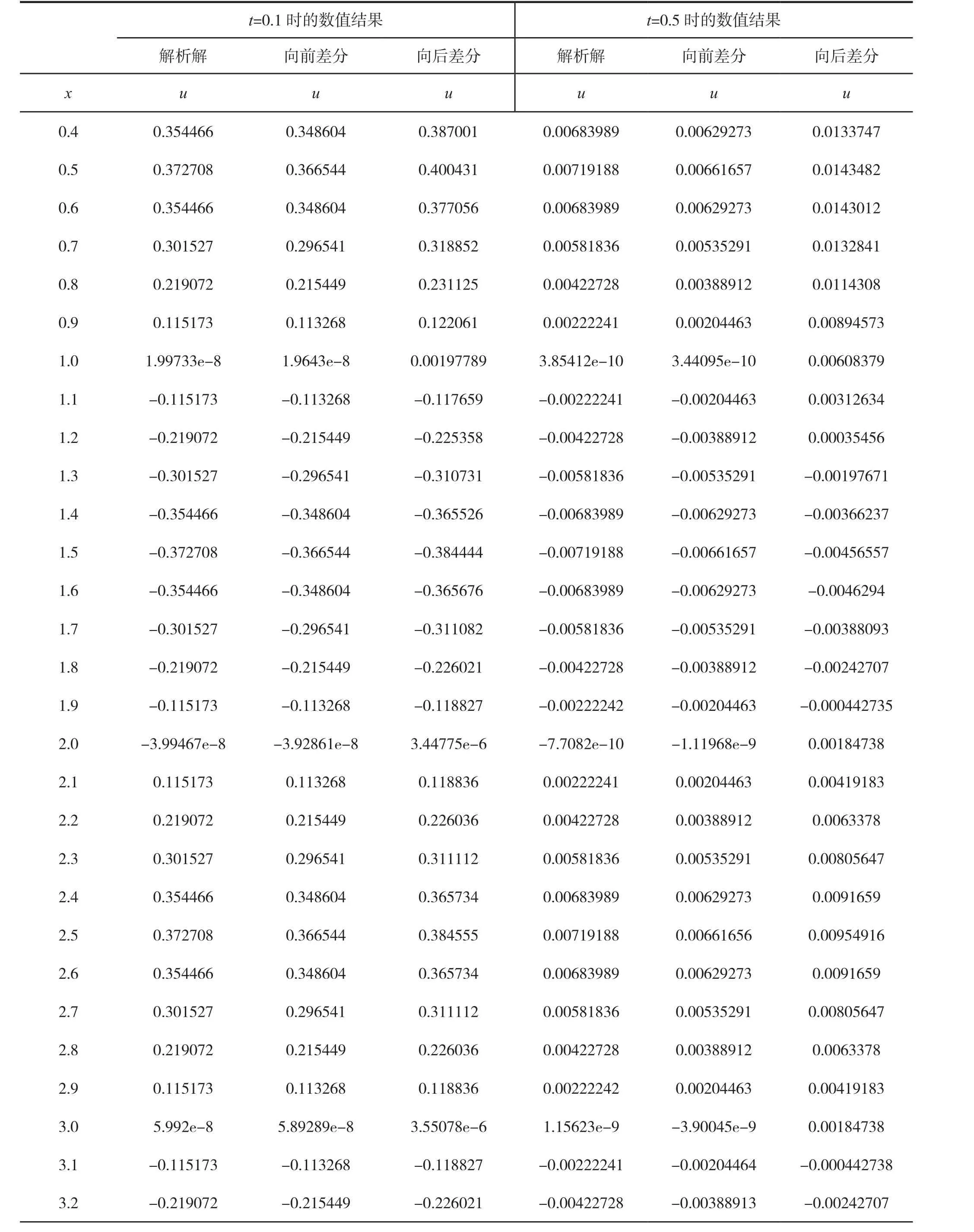
（续表2）

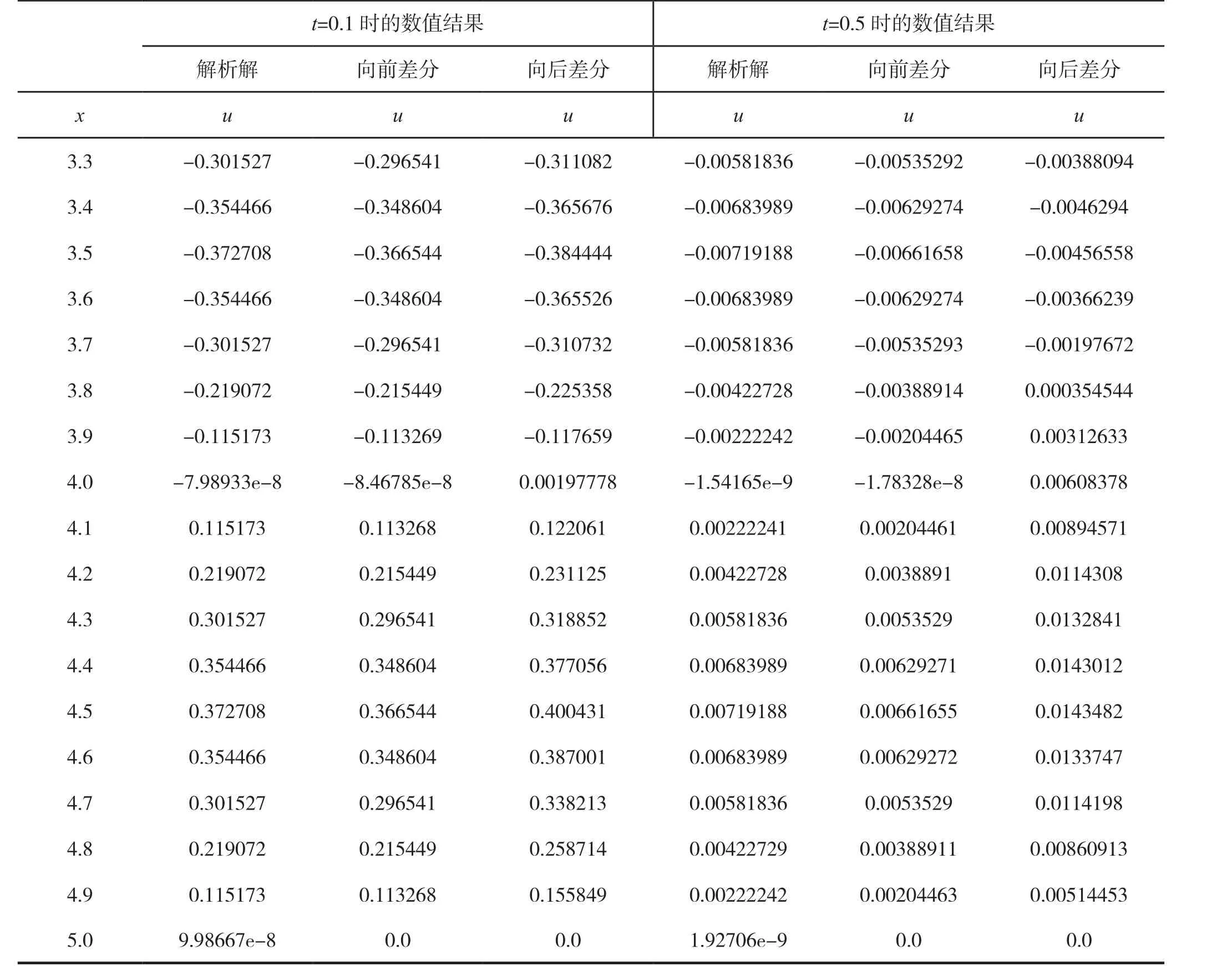
（续表2）

3 结论与展望

通过上面的讨论，可以看出，输运方程的数值解法需要考虑数值解的稳定性，对于本文中给出的两种差分方法，向前差分是条件稳定的，其稳定条件为a2λ≤0.5，而向后差分是绝对稳定的，在实际的数值计算中，两种差分格式如果对于空间变量x取相同的步长，向后差分对时间步长没有严格的限制，但是，向前差分就必须对时间步长加以限制，这样导致时间步长需要取的很小，就会大大提升计算量，而向后差分可以将时间步长取的相对较长，但这样的差分格式的计算精度不是很高，于是在很多需要高精度高效率的工程技术问题中，上面的方法实用性就变得比较有限了，所以我们需要寻找一些高效率高精度的计算方法来满足实际需求，比如加权隐格式，多层网格方法等，这将是我们接下来需要开展的工作。

［1］梁昆淼.数学物理方法［M］.北京：高等教育出版社，2002：459.

［2］徐长发，李红.微分方程数值解法［M］.武汉：华中科技大学出版社，2002：381.

［3］陆金甫，关治.偏微分方程数值解法［M］.北京：清华大学出版社，2007：82.

［4］Mitchell A R, Griffiths D F.The Finite Difference Methed in Partial Dofferential Equations［M］.New York： John Wiley & Sons, 1967:259.

［5］张文生.科学计算中的偏微分方程有限差分格式［M］.北京：高等教育出版社，2006：236.