环形定子的激光致表面波机理及可视化探测研究*

李方浩 章海军 张冬仙

(浙江大学,现代光学仪器国家重点实验室,杭州 310027)

1 引言

近年来,随着微纳米技术及微型光机电系统(MOEMS)的快速发展,对驱动技术也提出了新的要求.现有的驱动技术主要有电磁驱动、静电驱动[1]、压电驱动[2]、电热驱动[3]、光热驱动[4-7]等,其中电磁、静电、压电和电热等驱动方法需要采用导线将控制电流或控制电压引入到驱动机构中,因而无法真正实现非接触式的驱动控制;光热驱动采用将激光能量转换成热能的方法,实现对驱动机构的非接触控制,但是,受限于其所使用的光热转换机制,光和热的转换过程相对缓慢,这类光热驱动机构一般只能实现低速或低频驱动.因此,我们致力于研究发展一种基于激光致表面波的非接触式驱动方法,提出采用纳秒级超短脉冲激光激发出表面波,以此作为驱动源,实现对驱动机构(如马达)的驱动控制.

就激光激发声波这一物理特性而言,目前研究和应用较多的主要有光声光谱分析和激光超声探测等.光声光谱多用于对材料的成分、形貌及其他物理特性的分析,如多晶体材料弹性模量的研究[8]、薄膜机械和结构特性分析[9,10]、光声显微成像[11]等.激光超声探测利用光致超声波在待测物件内部传播时遇到疵点等损伤使其传播特性发生变化的原理,实现内部损伤的探测[12-14].本文所提出的基于激光致表面波的新型驱动方法,利用的是激光在物体表面(如定子)激发出表面波的椭圆形传播轨迹,实现对贴合在该物体表面的目标(如动子)的驱动.为此,本文开展了激光在环形定子表面激发表面波的物理模型及可视化实验研究,为发展光致表面波马达及驱动机构提供理论和实验基础.

2 原理与方法

2.1 环形定子的激光致表面波物理模型

当用脉冲激光照射固体材料表面时,材料将吸收光能形成局部热源并发生局部热膨胀;激光作用结束后,热源消失,该热膨胀区域发生收缩.这种周期性的膨胀和收缩运动将形成声场并向周边区域辐射声波,其中沿介质表面传播的弹性波称为表面波,它是表面纵波和沿垂直表面方向振动的横波叠加干涉的结果.

本文设计了一种带有凹槽阵列结构的环形定子,如图1所示,用脉冲激光照射该环形定子以激发表面波.图中,O为激光照射点,其位置取在圆环环带的中点处,以此为坐标原点建立直角坐标系,圆环内径为r1,外径为r2,C为凹槽阵列区域.

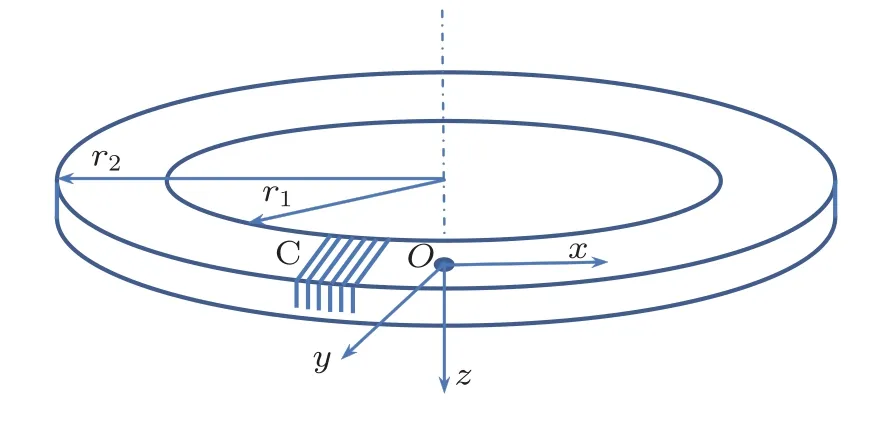
图1 带有凹槽阵列的环形定子示意图

脉冲激光照射O点时,在t时刻环形定子表面形成的热源方程为

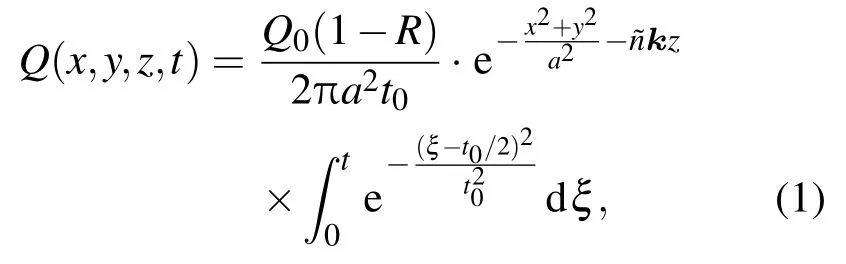
其中Q0是激光的单脉冲能量,R是反射率,a为光斑半径,t0为激光脉冲宽度,和k分别代表复折射率和波矢.

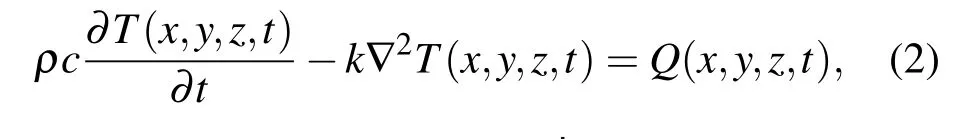
该热源在环形定子中发生热传导,形成温度场T(x,y,z,t),热传导方程为ρ,c,k分别为材料密度、比热容、热传导率,声场中表面波形变量Us(x,y,z,t)与温度T(x,y,z,t)服从热弹性方程[14]:

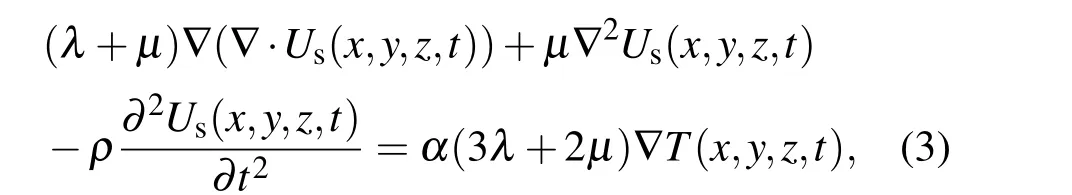
λ和µ为兰姆常数,α是热扩散系数.表面波在圆环内径和外径边界处以及凹槽边界处振幅为零,边界条件有:

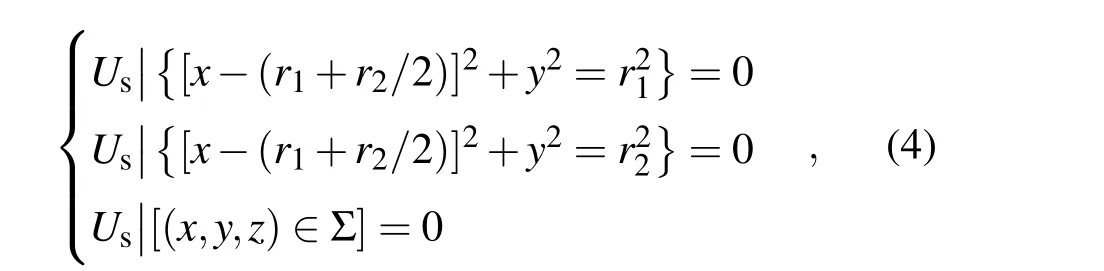
(4)式中Σ为齿状凹槽所形成的外表面.方程组(1),(2),(3)和边界条件(4)构成了激光在环形定子表面激发出的表面波的物理模型.该方程组通过有限元迭代方法进行仿真计算,得出激光在环形定子激发的表面波振幅近似正比于激光单脉冲能量Q0,热传导率k,反比于光照面积πa2,激光脉宽t0,比热c;振幅在z向随厚度的增加按指数衰减.因此,表面波传播到凹槽区域时将被凹槽阵列多次衰减和阻挡,表面波振幅值逐渐趋近于零,即表面波将不能穿过凹槽阵列区.

2.2 激光致表面波的动态可视化探测方法

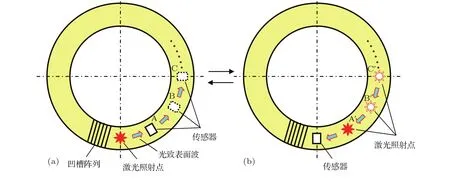
图2 激光致表面波在环形定子上传播的可视化探测原理

如图2(a)所示,激光激发出的表面波从照射点向外沿环形定子表面传播,由压电传感器在某一测量点探测并输入到计算机中.对于每一给定的测量点(如A点),表面波传播至该点的振动状态随时间的变化可以被准确地观测到;不断改变测量点的位置(如B和C点等),则可探测出表面波传播至环形定子表面所有的点的振动状态,而将所有这些点的波形信息整合起来,就可以对表面波的整体传播样貌进行分析.但是,不断移动传感器在圆环上的位置进行逐点探测,在实际操作中很难实现,而移动激光照射点则相对容易得多.因此,利用表面波在激光照射点和传感器探测点之间传播的可逆关系,可按图2(b)所示进行等效处理,将压电传感器置于原激光照射点处,而激光照射点在整个圆环面上逐点扫描,在每一点 (如 A′,B′,C′点等)激发出的表面波均由位置固定的传感器探测,并将探测到的波形信息收集,按时序重构各点的振动状态,即可等效地还原出由照射在传感器位置处的激光单脉冲激发的表面波在圆环面上的传播图样,从而实现激光致表面波的可视化探测.

3 实验与结果

实验中环形定子的材料选用热传导率相对较大、比热容相对较小的黄铜;圆环整体尺寸为外径40 mm,内径30 mm,厚度2 mm;在其环面上切割出6个相邻间距为0.5 mm,宽0.5 mm,深1.5 mm的凹槽,如图3所示.

图3 环形定子与压电传感器的布局图,白色矩形框内为激光扫描区域

采用波长1053 nm的脉冲激光器激发表面波,脉冲宽度为30 ns,单脉冲能量1 mJ,光斑直径约100µm.脉冲激光的重复频率为3 kHz,以保证有足够时间间隔探测每一发激光脉冲激发出的表面波的完整振动状态.图3中白色矩形框显示的是激光扫描区域,激光以光栅扫描方式扫描,扫描点间隔0.2 mm,扫描点数220×250.铜环放置在消声材料基座上,当激光扫描点落在铜环表面时,传感器可探测到表面波信号;而当激光点扫描到铜环以外的区域时,不产生表面波信号.由于激光扫描区域涵盖整个铜环结构,可保证整个铜环都能被扫描到,从而根据图2(b)所示的等效处理原理,实现激光致表面波在整个铜环表面上的动态传播过程的可视化.

压电传感器选用中心频率2 MHz的表面波斜探头,传感器左角与凹槽阵列的最近距离约为4 mm.

实验得到的光致表面波在环形定子上的可视化动态传播过程视频截图如图4所示.根据等效原理,当脉冲激光照射在传感器所处的位置时(以此时刻作为初始时间),表面波分别沿顺时针方向和逆时针方向在环形定子表面传播.图4(a)—(d)表明,沿顺时针方向的表面波传播到凹槽区域时消失,说明凹槽阵列对表面波有很好的阻挡和衰减作用,与理论分析一致;而沿逆时针方向的表面波可持续传播;在29.6µs时,波前传播到凹槽区域的另外一侧,完成近乎整周的单向传播,如图4(e)所示;在39µs之后,铜环面上的表面波因阻尼振荡而整体衰减,如图4(f).为实现表面波的持续单向传播,可选用适当频率的脉冲激光持续照射环形定子.

作为对比,选用相同尺寸但无凹槽结构的铜环进行了激光致表面波的可视化实验,实验结果如图5所示.根据等效原理,当脉冲激光照射在传感器所处的位置时,有两列光致表面波分别沿顺时针和逆时针方向传播;图5(a)—(d)表明,这两列表面波各自持续地向前传播,这与图4实验结果明显不同;在22.8µs时两列波开始汇合,见图5(d);之后出现相互混叠与串扰,如图5(e)和(f)所示,因此在该铜环上无法获得单向传播的激光致表面波.这一实验从另一侧面证明,凹槽阵列结构在获取单向传播的激光致表面波中的关键作用.

需要说明的是,图中沿顺时针方向的表面波在幅值上要弱于逆时针方向的表面波,这是由于作为传感器的斜探头在不同方向上探测能力不同而造成的.

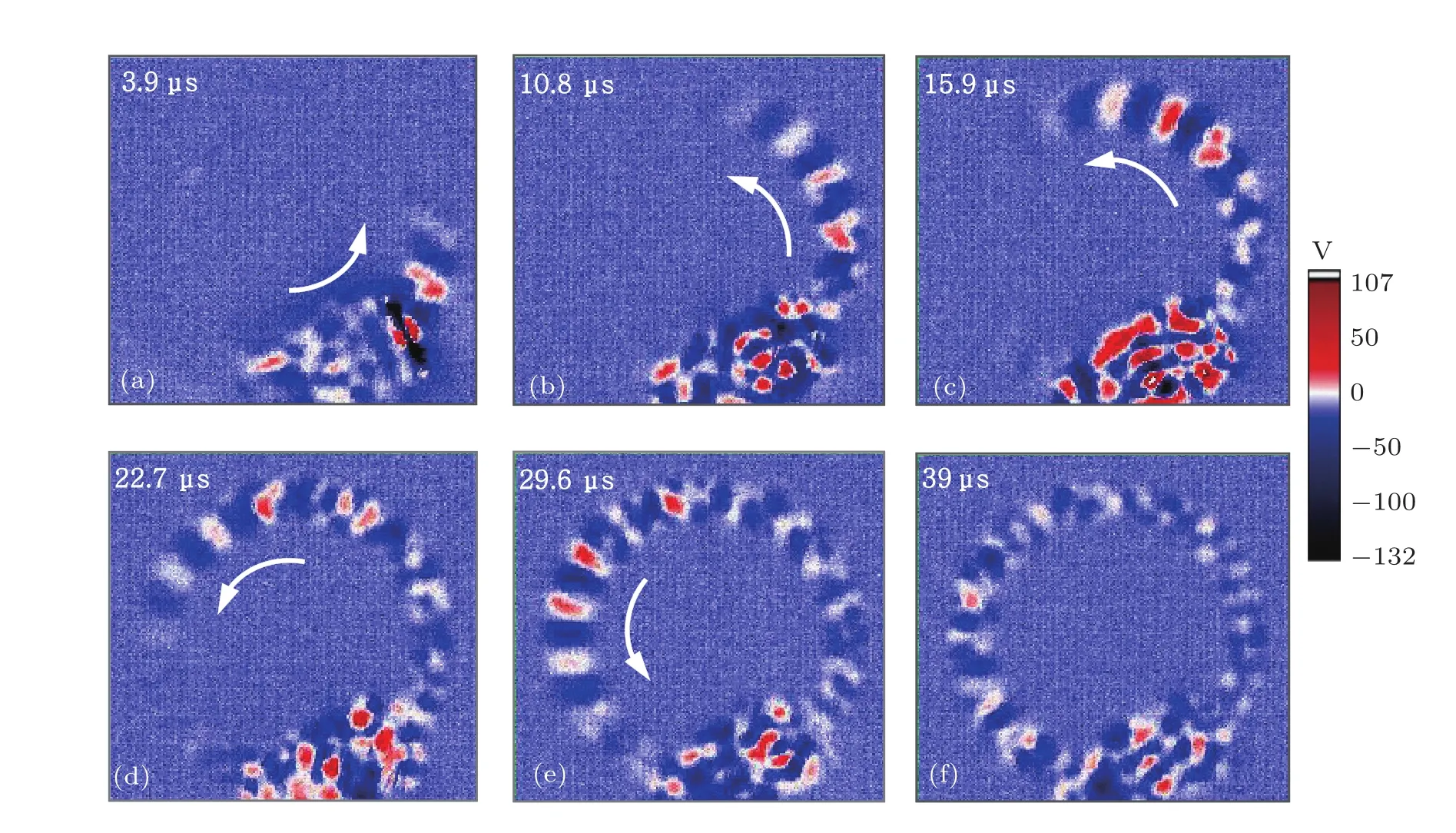
图4 激光致表面波在带有凹槽阵列结构的环形定子上单向传播的可视化视频截图

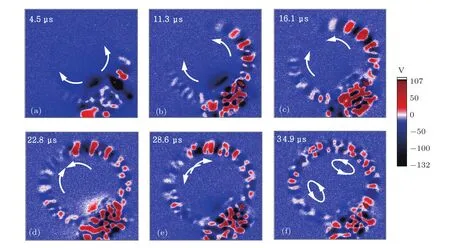
图5 激光致表面波在无凹槽结构的铜环上双向传播的可视化视频截图

4 结论

本文围绕激光致表面波的机理及传播特性开展了理论和实验研究,优化设计了带有凹槽阵列结构的环形定子,建立了激光在环形定子表面激发表面波的物理模型,给出了求解表面波幅值的方程组,并对影响表面波幅值的关键因素进行了分析.阐述了激光致表面波的动态可视化探测方法,利用表面波在激光照射点和传感器探测点之间传播的可逆关系,等效地还原出激光致表面波的传播图样,从而首次实现了激光致表面波在环形定子上传播的可视化探测.

采用这一可视化探测方法,在波长1053 nm,脉宽30 ns,单脉冲能量1 mJ的脉冲激光照射下,对表面波在铜材质的环形定子表面的传播特性进行了实验研究.理论与实验研究表明:当激发光斑的位置紧邻凹槽阵列时,沿着铜环向凹槽方向传播的表面波会被凹槽阵列迅速衰减和吸收,而沿着铜环向远离凹槽方向传播的表面波能够持续向前传递,据此实现了激光致表面波的单向传播;而对没有凹槽阵列结构的铜环进行的对比实验表明,激光致表面波在铜环表面双向传播,最终因相互混叠和串扰等而处于混乱状态.激光在该种环形定子表面激发出的单向表面波,将用于今后光致表面波马达及驱动机构的研究当中.

[1]Srinivasan P,Gollasch C,Kraft M 2010 Sens.Actuators A:Phys.161191

[2]Yang B,Liu J Q,Chen D,Zhou W M,Cai B C 2006 Chin.Phys.B 15454

[3]Hoxhold B,Buttgenbach S 2010 Microsyst.Technol.161609

[4]Wang L Y,Zhang D X,Zhang H J 2010 Appl.Phys.Lett.97131905

[5]Zhang D X,Zhang H J,Liu C 2008 Opt.Express 1613476

[6]Liu C,Zhang D X,Zhang H J 2009 Acta Phys.Sin.582619(in Chinese)[刘超,张冬仙,章海军2009物理学报582619]

[7]Zaidi S,Lamarque F,Prelle C,Carton O,Zeinert A 2012 Smart Mater.Struct.21115027

[8]Kautek W,Rudolph P,Daminelli G,Kruger J 2005 Appl.Phys.A 8165

[9]Giannetti C,Revaz B,Banf iF,Montagnese M,Ferrini G,Cilento F,Maccalli S,Vavassori P,Oliviero G,Bontempi E,Depero L E,Metlushko V,Parmigiani F 2007 Phys.Rev.B 76125413

[10]Ku G,Wang L V 2005 Opt.Lett.30507

[11]Callasso I G,Craig W,Diebold G J 2001 Phys.Rev.Lett.863550

[12]Zhao X Y,Gang T,Zhang B X 2008 Acta Phys.Sin.575049(in Chinese)[赵新玉,刚铁,张碧星2008物理学报575049]

[13]Xiao Q,Wang J,Guo X S,Zhang D 2013 Acta Phys.Sin.62094301(in Chinese)[肖齐,王珺,郭霞生,章东2013物理学报62094301]

[14]Pei C X,Fukuchi T,Zhu H T,Koyama K,Demachi K,Vesaka M 2012 IEEE Trans.Ultrason.Ferroelectr.Freq.Control 592702