基于Bode图的数控转台伺服动刚度分析方法

尹 明 范丽鹏

（内蒙古科技大学机械工程学院，内蒙古包头 014010）

数控转台的传统驱动方式通常是旋转伺服电动机加齿轮、齿轮齿条副及蜗杆齿轮副等，由于存在机械传动链，虽有较好的静态刚度，但在完成启动、加速、减速、反转及停车等运动时，会产生弹性变形、摩擦和反向间隙等，造成机械振动、运动响应慢、动态刚度差及其他非线性误差，难以实现数控转台的高精度加工［1］。直接驱动技术在一定程度上解决了上述问题，它消除了中间传动环节，具有推力大、响应速度快、加速度及定位精度高等特点，但干扰信号将无缓冲地作用在电动机上，使系统易受负载扰动及参数变化等不确定性的影响，这大大降低了系统的抗干扰性能和跟随性能［2］。为了分析负载扰动及参数变化对系统的影响，提高系统伺服刚度，本文推导出系统的传递函数及由干扰输入引起的位置输出的传递函数模型，利用Matlab软件对模型进行了仿真，通过Bode图分析了负载扰动及参数变化对系统伺服刚度的影响规律，进而可以有针对性地进行参数整定，从而提高系统的抗干扰性能。

1 干扰输入引起的位置输出的传递函数框图

基于PID控制的永磁同步电动机转台伺服系统通常包括电流环、速度环和位置环3层控制环节［3］，综合电流环、速度环和位置环的控制结构图，适当简化后，得到其控制系统传递函数框图如图1所示。其中控制系统参数分别是:位置环比例增益Kv、速度环比例增益Kp、速度环积分时间常数Tn、电流环比例增益Ki、转矩系数Kf、系统转动惯量J以及粘滞阻尼系数B。

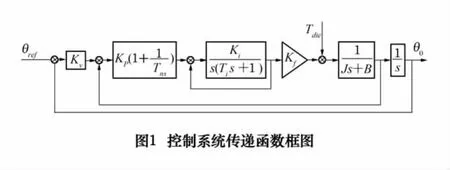
电流环闭环传递函数为

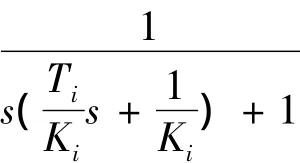
通常电流环闭环传递函数可降阶近似为

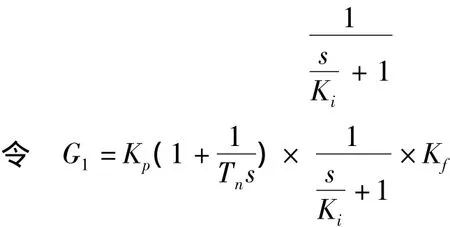
通过等效变换可以得到系统干扰输入引起的位置输出的传递函数框图如图2所示。

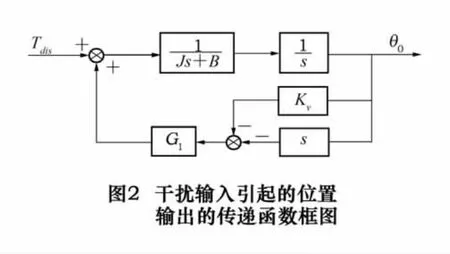
2 系统伺服刚度分析

伺服刚度即系统受到的干扰力矩与干扰力矩引起的位置误差之比，也就是输入为零时的干扰力矩与干扰力矩引起的输出之比，即为从干扰到输出传递函数的倒数［4］，系统伺服刚度越高，其抵抗干扰的能力就越强，表现在Bode图中，即伺服刚度越高，系统干扰所引起的输出偏差越小，系统在相同频率干扰下Bode图的幅值越小。

由控制系统传递函数框图可知，影响伺服刚度的主要参数有Kv、Kp、Tn、Ki和J。对于已选定转台系统，电磁转矩系数Kf是固定的，参考文献［5］中所使用的数控转台参数，本文取Kf值为9.4 N·m/A，B值为0.09 N·m·rad/s，Ki为 1 000 V/A，Kv为 750 min，Kp为45 min/rad，Tn为 10 ×10－3s，J为 50 kg·m2。通过调用Matlab软件中的Bode图函数可求解和绘制系统Bode图。下面将采用单因素仿真分析法研究这些参数对系统伺服刚度的影响。

（1）改变系统位置环比例增益Kv，使其从1开始以200为步长逐渐增加到3 000，系统的Bode图变化如图3所示。由图3可知，随着Kv的增加，系统在低于103Hz的中低频段的幅值在相应减小，而在其他频段内，Bode图幅值基本没有变化，说明随着Kv的增加系统抵抗中低频段干扰的能力在增加，伺服动刚度增加。

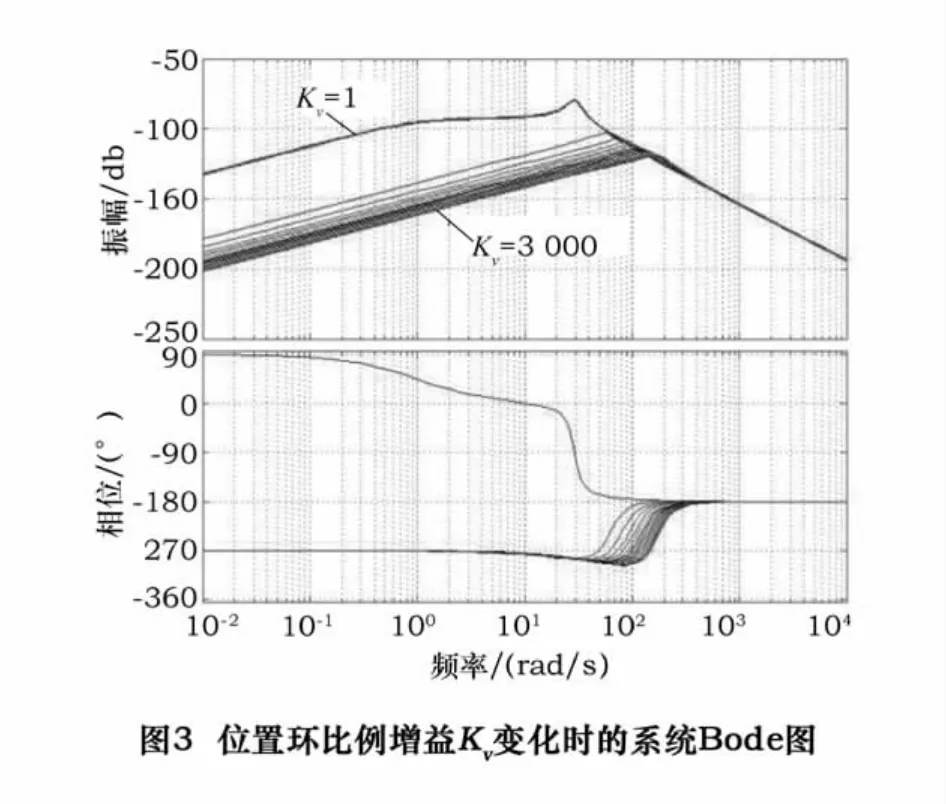
（2）改变系统速度环比例增益Kp，使其从1开始以70为步长逐渐增加到1 000，其余系统参数不变，系统的Bode图变化如图4a所示。由图4a可知，随着Kp的增加，系统在低于103Hz的中低频段的幅值在相应减小，而在其他频段内，Bode图幅值基本没有变化，说明随着Kp的增加系统抵抗中低频段干扰的能力在增加。由图4b可以清楚看到随着Kp的增加，Bode图幅值在特定频段内有明显增大的趋势，系统开始出现超调，变的越来越不稳定，可见，增加系统位置环比例增益可以对系统中低频干扰有明显抑制作用，但要适当取值，以免影响系统稳定性。

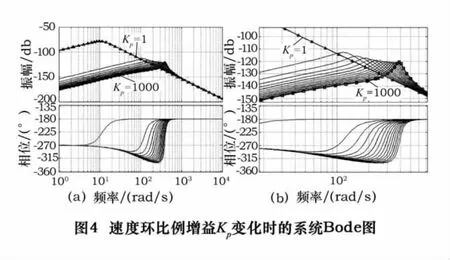
（3）改变系统速度环积分时间常数Tn，使其从0.001开始以0.01为步长逐渐增加到0.2，其余系统参数不变，系统的Bode图变化如图5所示。由图5可知，随着Tn的增加，系统在低于5×102Hz的中低频段的幅值在相应增大，而在其他频段内，Bode图幅值基本没有变化，说明随着Tn的增加系统抵抗中低频段干扰的能力在减少，伺服动刚度降低。与此同时，随着Tn的增加，Bode图幅值在特定频段内有明显增加的趋势，系统开始出现超调，变的越来越不稳定，可见，在适当范围内降低速度环积分时间常数值可以对系统中低频干扰有明显抑制作用。

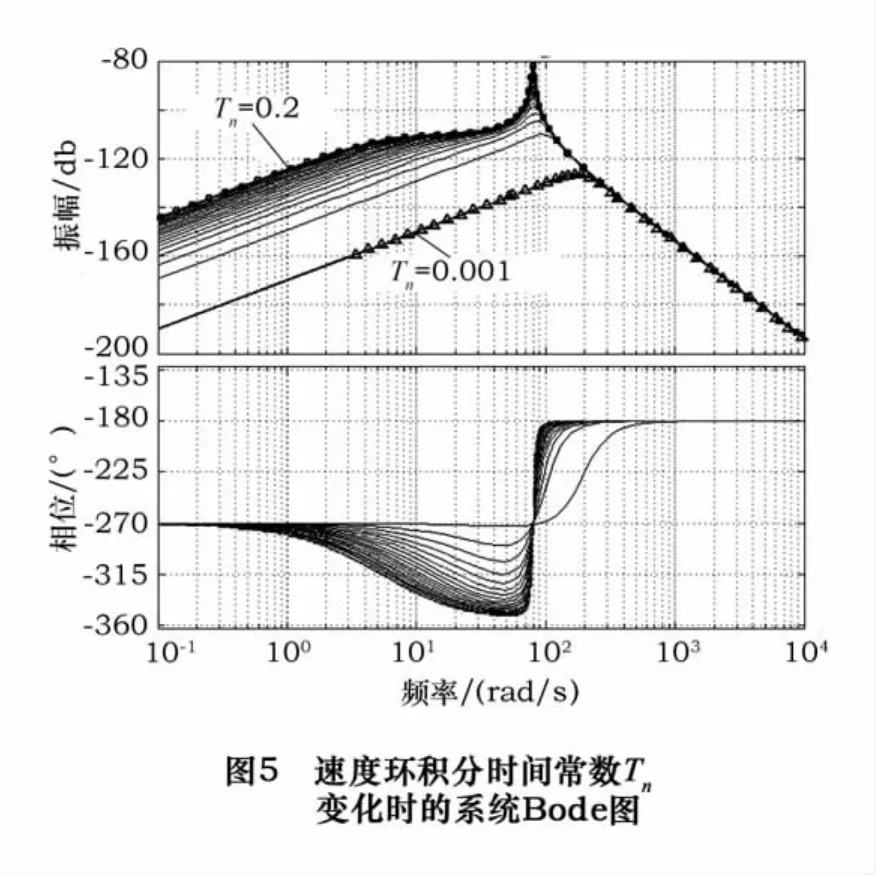
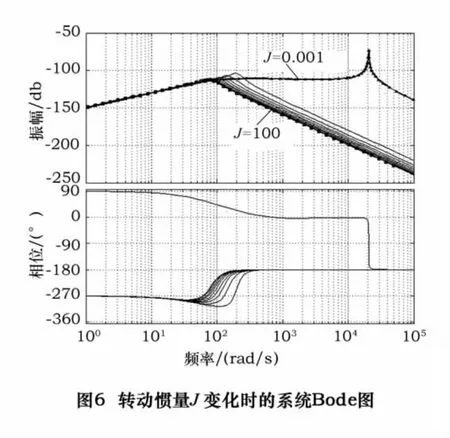
（4）改变系统转动惯量J，使其从0.001开始以10为步长逐渐增加到100，其余系统参数不变，系统的Bode图变化如图6所示。由图6可知，随着J的增加，系统在高于102Hz的中高频段的幅值在相应减小，而在其他频段内，Bode图幅值基本没有变化，说明随着J的增加系统抵抗中高频段干扰的能力在增加，系统动刚度增加，与此同时，随着J的增加，Bode图幅值也趋于平稳，系统趋于稳定。可见，在适当范围内增加系统转动惯量可以对系统中高频干扰有明显抑制作用，也会提高系统稳定性。

3 结语

为了得到控制系统参数对伺服动刚度的影响，提高直接驱动数控转台的伺服动刚度，本文提出了基于Bode图分析系统伺服动刚度的方法。通过上述推导和仿真分析，可以得到如下结论:

（1）对于中低频扰动，可以通过适当增加位置环比例增益、速度环比例增益或者降低速度环积分时间常数来提高系统伺服动刚度，对于高频扰动，可以通过适当增大系统的转动惯量来提高系统伺服动刚度。

（2）虽然本文中分析系统伺服动刚度的方法是针对直接驱动数控转台系统，但该分析方法具有普遍应用的意义，同样可以应用在其他电动机驱动的系统中，以提高系统伺服动刚度。

［1］廖效果，朱启逑．数字控制机床［M］．武汉:华中理工大学出版社，1999．

［2］Wen Zhaofang，Chen Peizheng，Wang Xiankui．Current compensation in the control of high thrust permanent magnet linear synchronous motor［J］．Transactions of Beijing Institute of Technology，2004，24（3）:233－237．

［3］George Ellis．Control system design guide 3rd edition［M］．Academic Press，2004．

［4］David M．Alter，Tsu－Chin Tsao．Stiffness enhancement of direct linear motor feed drivers for machining［C］．Proceedings of the American Control Conference Baltimore:1994．

［5］徐冬生．直接驱动数控转台低速转矩脉动抑制研究［D］．沈阳:沈阳工业大学，2008．