改进的DRASTIC模型在地下水易污染性模糊评价中的应用

郝 静，张永祥，丁 飞，白玉华，任仲宇，巩奕成(1.北京工业大学建筑与工程学院，北京 100124；2.水质科学与水环境恢复工程北京市重点实验室，北京 100124）

“地下水易污染性”的概念是由美国环保署EPA于1987年提出［1～2］:它是指污染物从地表迁移到含水层的难易程度。各类含水层的易污染性统称为地下水易污染性。

地下水易污染性包括:本质易污染性和特殊易污染性［1～5］。本质易污染性是只考虑水文地质内部因素的易污染性而不考虑人类活动和污染源类型影响，水文地质内部因素有相对静态性、不变性及人为不可控制性的特点。地下水对某一特定污染源或人类活动的易污染性称为特殊易污染性，特殊易污染性的易污程度因污染源类型和人类活动的不同而不同，它具有动态性、可变性和人为可控性的特点［6］。

1 DRASTIC模型简介

1.1 DRASTIC模型

DRASTIC模型是评价地下水易污染性的一种指标体系法，主要考虑7个参数:D(depth to water)为含水层埋深；R(net recharge)为含水层净补给量；A为含水层介质类型(aquifer media)；S为土壤介质类型(soilmedia)；T为地形坡度(topography)；I为包气带影响(impact of the vadosezone media)；C为含水层渗透系数(conductivity of the aquifer)。以上7项参数中，4项参数可定量获得，3项参数不能定量获得，参数的范围、评分及权重见参考文献［7］。DRASTIC模型依据地下水易污染性指数来判断相应地区的地下水易污染性［7］。一般易污染性指数高的区域地下水相对容易遭受污染［8］。地下水易污染性指数由各参数定额与权重的线性加权和构成(式1)。对某一区段的地下含水层j，其易污染性指数可表示为［9］:

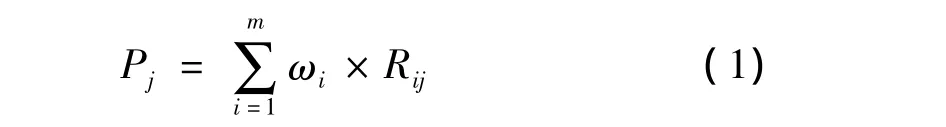
式中:Pj——地下水含水层j易污染性指数；

ωj—— 指标 j的权重；

Rij——含水层样本j第i个指标所赋的定额。

1.2 DRASTIC评价方法的局限性及其改进方法

考虑到DRASTIC 计算方法存在较多缺陷［10～11］，本文对模型作改进:

(1)运用模糊理论将DRASTIC指标体系进行定额，克服指标定额不连续性变化的缺陷。

(2)以含水层厚度(M)代替含水层介质(A)。含水层厚度越厚，其稀释能力越强，含水层厚度的范围及评分，见表1。

(3)引用陈守煜提出的语气算子比较法确定地下水易污染性评价指标的权重［12］。

2 模糊综合评价模型

2.1 构建各评价样本评价指标的实测值矩阵

实测值矩阵xij是由n个待判定的样本及反映样本易污染性的m个指标构成。

式中:xij——样本j指标i的实测值；

i=1，2，…，m；j=1，2，…，n，n 为样本数。

2.2 构建指标标准值矩阵

构建m×c阶指标标准特征值矩阵是将含水层易污染性评价样本j依据m项指标值，按c个等级级别标准值进行识别构成［12］:

式中:yih——指标i级别h的标准特征值。i=1，2，…，m；h=1，2，…，c。

根据陈守煜给出的DRASTIC模型7项指标10个级别(m=7，c=10)的指标标准特征值进行改进(表2)，同时确定与各级别对应的语气算子(表3)。

2.3 级别相对隶属度的确定

根据指标特征值与指标标准值建立某种指标对地下水易污染性等级的隶属函数。10个级别的指标标准特征值对模糊概念极难污染(1级)的相对隶属度即为级别相对隶属度［11］。级别相对隶属度介于0～1之间，是线性变化的:

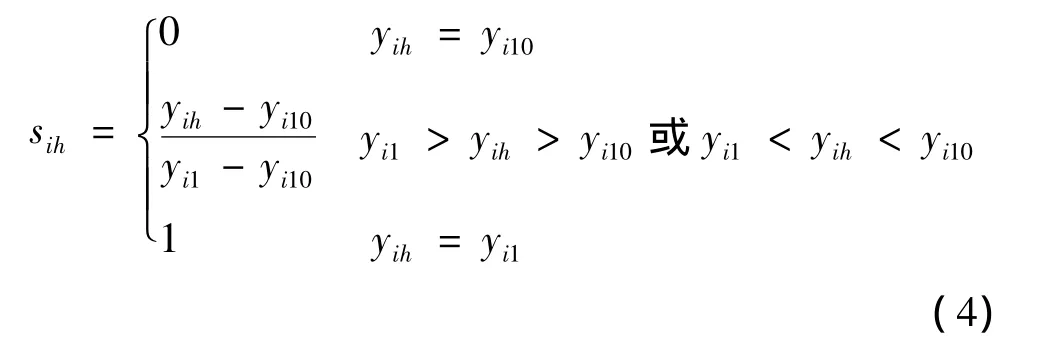
式中:sih——指标i级别h的标准特征值的级别相对隶属度。

yi1、yi10分别为指标i的1级、10级标准值。根据式(3)已知指标的标准特征值矩阵，结合式(4)对极难污染的相对隶属度函数即可得出对极难污染的指标标准特征值的相对隶属度矩阵［11～14］:

2.4 各指标相对隶属度的确定

样本j指标 i对易污染性的相对隶属度函数(rij)［7］。可表示为:

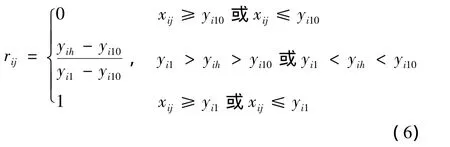
式中:rij——相对隶属度函数(rij)中，样本 j指标 i的特征值。

表1 含水层厚度等级分值及权重Table 1 Quantitative values and weights of the thickness of the aquifer

表2 DRASTIC模型7指标各级别标准特征值Table 2 Seven indexes standard eigenvalues of each level of the DRASTIC model

表3 各级别相应语气算子Table 3 Correspondence relationship between the mood operator and the levels

应用式(6)，可得出式(2)中样本集矩阵的指标相对隶属度矩阵R:

由矩阵R知样本j的7个指标相对隶属度:

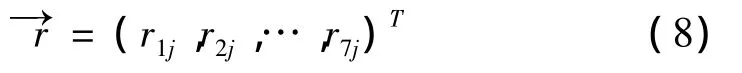
级别限的确定:首先，将行向量rj中指标1，2，…7的相对隶属度r1j，r2j，…，r7j分别与矩阵S中的七个行向量进行逐一比较；再根据其上下限范围，可确定rj落在矩阵S的级别限在级别下限aj与级别上限bj之间。

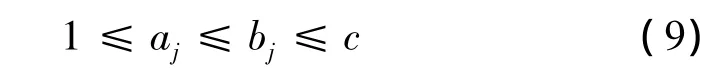
式中:aj——级别下限；

bj——级别上限；

c——级别上限最大值。

2.5 各评价指标归属于各个级别的最优相对隶属度

矩阵的确定［12］

基于DRASTIC的7项指标，设指标权向量为:

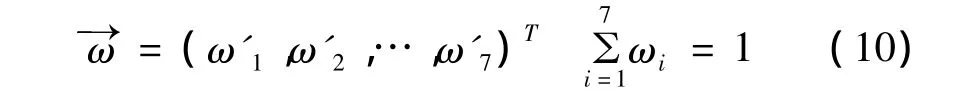
样本j与级别h之间存在的差异，常用广义欧氏距离表示［12］:

式中:dhj——广义欧氏距离。

欧氏距离中包含了指标权重的因素。本文以样本j归属于级别h的相对隶属度uhj为权重，将样本j与级别h之间的差异表示地更为合理［12］。

式中:uhj——样品j归属于级别h的隶属度函数。h=1，2，…，10；j=1，2，…，n。

隶属度与欧氏距离关系的完整形式为:

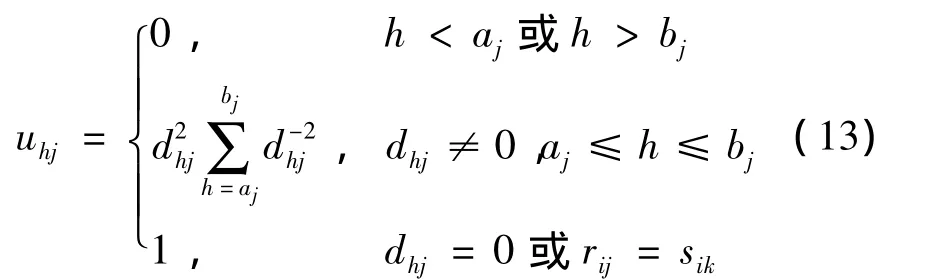
根据式(13)可得n个样本集与10个级别对应关系的最优相对隶属度矩阵为［9］:

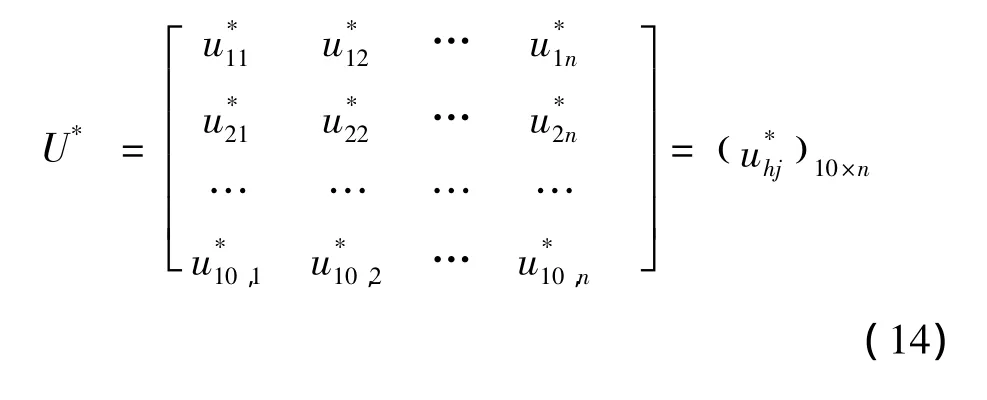
式中:uhj——样本j对级别h的相对隶属度。h=1，2，…，10；j=1，2，…，n。

各级别特征值［11］:

上式计算结果可反映的样本集关于含水层易污染性的程度:H值越大，则含水层易污染性越强。最小级别特征值:Hmin=mjin Hj对应的样本受到污染的可能性最小。

3 实例应用

本次地下水的易污染性评价，以北京市朝阳区为研究区，本区地势低，地面坡降平缓，有零星坡岗地，地貌属洪积冲积扇，第四系覆盖层厚100～450m，表层土质主要为壤土，土地肥沃。选取了5个水文地质区段(样本)，7项评价指标特征值列于表4。

3.1 相对隶属度矩阵R的计算

根据研究区样本集的指标特征值表4，所提供指标的特征值信息，得矩阵X(式16)，结合指标对极难污染相对隶属度函数(式6)可得相应矩阵R(式17)。

3.2 标权向量的确定

3.2.1 定性排序以确定各指标重要性

依据以往经验知识，结合研究区域的水文地质条件，依次对7项评价指标的重要性做比较［12］，得出相对重要性排序标度矩阵(式18):

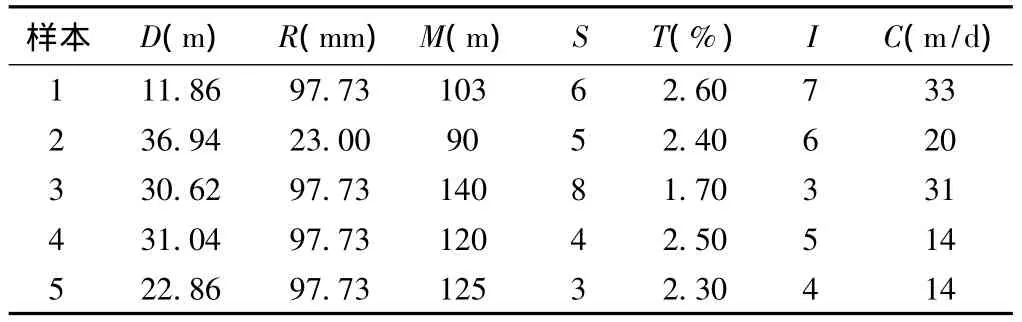
表4 研究区样本集的七项指标特征值Table 4 Index matrix of the samples

矩阵 E 各行之和依次为6，4.5，3，1.5，0.5，6，3。可得指标重要性的定性排列次序为:含水层埋深(D)、包气带影响(I)＞含水层净补给量(R)＞含水层厚度(M)、含水层的水力传导系数(C)＞土壤介质类型(S)＞地形坡度(T)。

3.2.2 七项指标重要性的相对隶属度

根据以上定性排序结果，含水层埋深(D)为最重要的指标，以其作为比较标准，依次与其他6项指标进行二元比较，参考评价区域的实际情况及相关经验知识，经综合考虑判断后，得到指标对重要性的相对隶属度即非归一化指标权重，进一步得归一化权重［12］(表5)。

表5 基于语气算子法的权重计算Table 5 Weight calculation based on the modal operator method

3.2.3 计算各样本对级别h的相对隶属度根据矩阵式(14)得U*(式19)。

由式(19)各列相加，所得样本各级别相对隶属度之和，可得样本集的级别特征值向量:

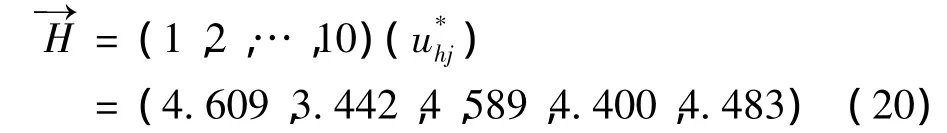
地下水易污染性隶属度和易污染性排序(表6)，可知在研究区的5个水文地质区样本集中地下水易污染性评价特征值均不超过5级，参考表3中对应关系，样本大多处于略难与微难污染之间，偏向微难污染。其中，样本2对应含水层最不易污染，其评价特征值小于4级，介于难污染和略难污染级别之间，但较偏向难污染。

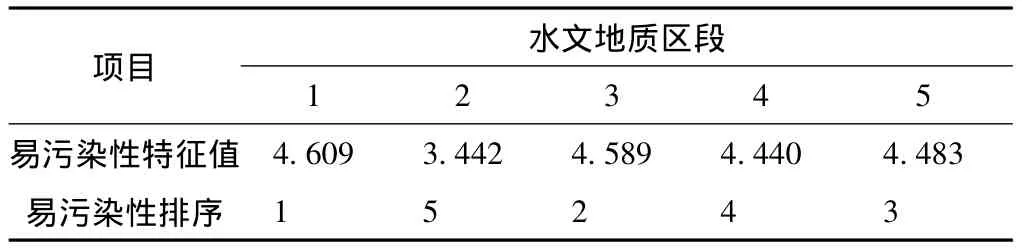
表6 模糊综合评价模型地下水易污染性隶属度和易污染性排序Table 6 Relative membership degree and order with the fuzzy pattern recognition model

为验证本方法的真实性，参照已有研究区样本水质评价综合指标法F值的计算结果(表7)，可见样本2的综合水质最好。

表7 样本综合评价分值Table 7 Values of comprehensive evaluation of the sample

为进一步验证本次改进的评价方法，本文将评价结果与常规DRASTIC法进行对比。给出样本定额值与权重值(表8)，根据式(1)计算，得出5个样本的易污染性特征值(表 9)［13～14］。样本的易污染性排序为:(1，5，2，4，3)，其中样本2易污染性指数最低最不易受污染。

综上，可知本次改进的评价方法可靠，结果合理，基本符合研究区实际情况。

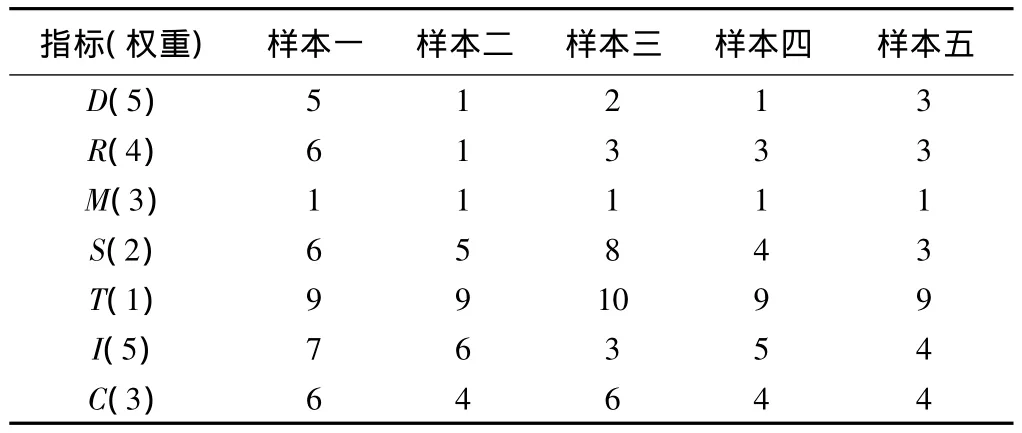
表8 样本定额值Table 8 Rating of the samples

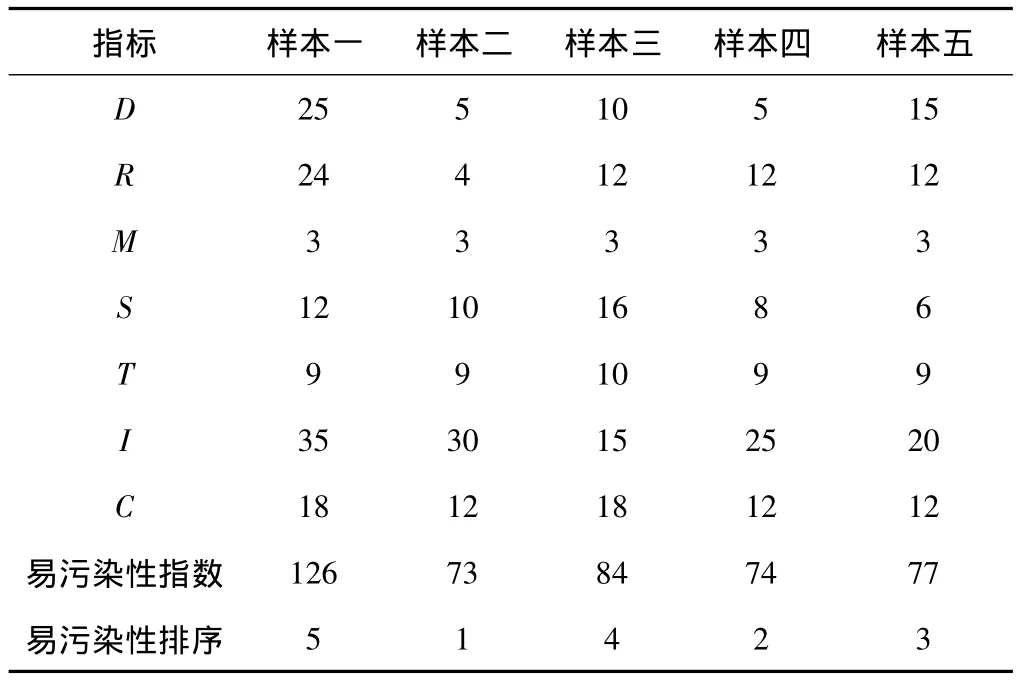
表9 研究区样本易污染性指数Table 9 Vulnerability index of the samples

4 结论

鉴于地下水易污染性评价影响因素较多且复杂，而地下水易污染性本身就是一模糊概念，本文依据模糊集理论，对DRASTIC模型进行了改进。将改进的模型应用于研究区地下水易污染性评价，通过与研究区水质评价结果的验证，以及与传统DRASTIC方法的对比，总结出改进的模型具有如下优点:

(1)采用模糊隶属度进行定额，体现了指标的连续变化对地下水易污染性的评价结果的影响。

(2)以含水层厚度(M)代替含水层介质类型(A)克服了该指标难以准确获取且不直接影响含水层易污染性的缺点，使评价结果更客观。

(3)应用语气算子比较法确定易污染性评价各指标权重，简化了计算，提高了评价的准确性。

综上，该方法理论分析严谨，物理概念清晰，应用于对地下水易污染性进行评价，能够较为客观地反应实际情况。

［1］Aller I，Bennet T，Lehr J H，et al.DRASTIC:a standardized system for evaluating groundwater pollution potentialusing hydrogeologic settings［R］.U.S.EPA Report，1987.

［2］Lobo-Ferreira J P， Oliveira M M. DRASTIC groundwater vulnerability mapping of Portugal［C］//Pro ceedings，Congress of the International Association of Hydraulic Research.IAHR Part C，1997:132－ 137.

［3］范琦，王贵玲，蔺文静，等.地下水易污染性评价方法的探讨及实例［J］.水利学报，2007(5):94－98.［FAN Q，WANG G L，LIN W J，et al.New method for evaluating the vulnerability of groundwater［J］.Journal of hydraulic engineering，2007(5):94 － 98.(in Chinese)］

［4］Youn Jong Kim，Se-Yeong Hamn.Assessment of the potential for groundwater contamination using the DRASTIC/EGIS technique，Cheog ju area，South Korea［J］.Hydrogeology Journal，1999(7):227 － 235.

［5］孙才志，左海军，栾天新.下辽河平原地下水易污染性研究［J］.吉林大学学报:地球科学版，2007(5):105 － 110.［SUN C Z，ZUO H J，LUAN T X.Research on Groundwater Vulnerability Assessment of the Lower Liaohe River Plain［J］.Journal of Jilin University:Earth Science Edition，2007(5):105 －110.(in Chinese)］

［6］范弢，杨世瑜.云南丽江盆地地下水易污染性评价［J］.吉林大学学报:地球科学版，2007(3):137－142.［FAN T，YANG S Y.Groundwater Vulnerability Assessment in Lijiang Basin［J］.Journal of Jilin University:Earth Science Edition，2007(3):137 －142.(in Chinese)］

［7］周惠成，王国利.基于DRASTIC模型含水层易污染性模糊综合评价［J］.大连理工大学学报，2001(2):89 － 92.［ZHOU H C，WANG G L.Fuzzy comprehensive evaluation model for assessing groundwater vulnerability based on the DRASTIC system［J］. Journal of Dalian University of Technology，2001(2):89－92.(in Chinese)］

［8］雷静，张思聪.唐山市平原区地下水易污染性评价研究［J］.环境科学学报，2003(1):96－101.［LEI J，ZHANG S C.Study on the groundwater vulnerability assessment in Tangshan plain area［J］.Journal of Environmental Sciences，2003(1):96－101.(in Chinese)］

［9］方樟，肖长来，梁秀娟，等.松嫩平原地下水易污染性模糊综合评价［J］.吉林大学学报，2007(3):546－550.［FANG Z，XIAO C L，LIANG X J，et al.Fuzzy Comprehensive Evaluation of the Groundwater Vulnerability in Songnen Plain［J］.Journal of Jilin University:Earth Science Edition，2007(3):546－550.(in Chinese)］

［10］鄂建，孙爱荣，钟新永.DRASTIC模型的缺陷与改进方法探讨［J］水文地质工程地质，2010，37(1):102 － 107.［E J， SUN A R，ZHONG X Y.Inadequacies of DRASTIC model and discussion of improvement［J］.Hydrogelogy ＆ Engineering Geology，2010，37(1):102 －107.(in Chinese)］

［11］李绍飞，孙书洪，王勇.基于DRASTIC的含水层易污染性模糊评价方法与应用［J］.水文地质工程地质，2008，35(3):112 － 117.［LI S F，SU S H，WANG Y.Application of themethod forfuzzy assessment of aquifer vulnerability based on DRASTIC［J］.Hydrogeology ＆ Engineering Geology，2008，35(3):112 －117.(in Chinese)］

［12］陈守煜，伏广涛，周惠成，等.含水层易污染性模糊分析评价模型与方法［J］.水利学报，2002，7(23):23 － 30.［CHEN S Y，FU G T，ZHOU H C，et al.Fuzzy analysis model and methodology for aquifer vulnerability evaluation［J］.Journal of hydraulic engineering，2002，7(23):23 －30.(in Chinese)］

［13］陈浩，王贵玲，侯新伟，等.城市周边地下水系统易污染性评价-以栾城县为例［J］.水文地质工程地质，2006，33(5):103 －105.［CHEN H，WANG G L，HOU X W，et al.The groundwater vulnerability assessment of the district around city taking Luancheng County as an example［J］.Hydrogelogy＆ Engineering geology，2006，33(5):103 －105.(in Chinese)］

［14］曲文斌，王欣宝，钱龙，等.石家庄城市区地下水易污染性评价研究［J］.水文地质工程地质，2007，34(2):6 －9.［QU W B，WANG X B，QIAN L，et al.Frangibility evalution of the ground water in Shijiazhuang city［J］.Hydrogeology ＆ Engineering Geology，2007，34(2):6 －9.(in Chinese)］