地下水污染监测网多目标优化设计模型及进化求解

骆乾坤，吴剑锋，林 锦，祝晓彬，吴吉春

（1.南京大学地球科学与工程学院水科学系，江苏 南京 210093；2.南京水利科学研究院，江苏 南京 210029）

在地下水污染治理和修复过程中，建立相应的地下水污染长期监测网络，可以及时获取地下水的物理、化学、生物特性的动态变化资料，从而保证治理结果的可靠性［1］。自20世纪80年代国外就有地下水污染监测网设计的研究报道，随后国内也开展了这方面的研究［2～5］。近10多年来，地下污染监测网设计研究已成为地下水领域的研究热点之一［6～10］。目前，地下水污染监测网的设计多采用模拟-优化方法［11］。

在处理地下水污染监测网优化设计问题时，决策者往往需要权衡各方面因素的相互影响。在这种情况下，采用多目标优化方法求解出相互矛盾的目标函数之间的权衡曲线可以提供给决策者一系列的Pareto解，以便其根据实际需要选择一个最有效、最合适的解。但传统地下水污染监测网优化设计大多数都是建立在单一目标函数优化基础上的罚函数方法［7～9］。通常情况下如果对罚函数选取不当，优化算法就很可能陷入局部最优解，然而对于一个给定的目标函数来说，很难找到适合的罚函数。将单一目标优化问题多目标化就可以克服以上问题［12］。多目标优化方法可以同时优化所有的目标函数，而不需要知道各个目标函数的权重或者处理为约束条件。为此，近年来，各种多目标进化算法已逐渐应用到地下水资源模拟优化领域。如，Ritzel等［13］将多种遗传算法应用到目标函数分别为最小化治理成本和最大化去除污染物的地下水污染治理问题，结果表明Pareto遗传算法(Pareto genetic algorithm，PGA)比其他算法更为优越。Erickson等［14］将小生境Pareto遗传算法(niched Pareto genetic algorithm，NPGA)引入到地下水水质管理领域，场地实验优化结果表明与单目标遗传算法和随机搜索算法相比，NPGA可以得到更加完整的权衡曲线。吴剑锋等［15～16］针对NPGA算法存在局部早熟收敛和收敛速度慢两个不足，提出了改进NPGA(improved NPGA，INPGA)方法。二维理想算例和三维实际算例的优化结果均表明该算法求解过程简单，计算时间短，优化得到的Pareto解集权衡曲线的跨度更为合理。

本文采用模拟-优化方法建立地下水污染监测网设计的多目标优化模型，同时引入INPGA方法用于求解监测网的多目标优化设计模型，并通过算例应用对其进行分析和验证。

1 多目标优化问题概述

一般多目标优化问题可描述为:最小化:

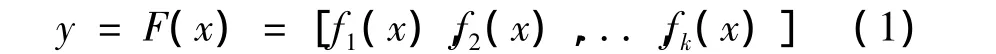
约束条件:

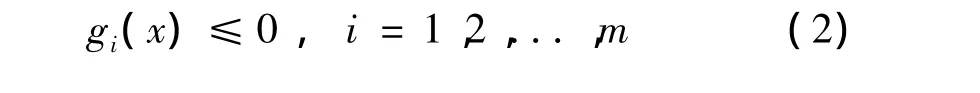
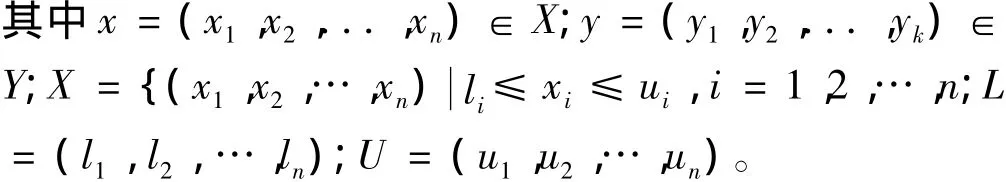
以上多目标优化问题由k个目标函数fk(x)或yk，n个决策变量xn和m个约束条件组成。X表示决策空间，ln和un分别为变量xn的下界和上界，L和U分别是决策变量xn的下界和上界向量，Y表示目标函数空间。对于任意两个向量 y=(y1，y2，...，yk)和 y'=(y'1，y'2，...，y'k)，如果任意 i∈ {1，2，...，k}，有 yi≤ yk'成立，同时存在 i∈ {1，2，...，k}，使得 yi≤ yk'成立，亦即向量y在所有的目标函数中至少不劣于向量y'，且至少有一个目标函数优于向量y'，则称向量y优于或控制向量y'。

对于以上多目标优化问题，如果存在x*∈X，同时当且仅当不存在x∈X，使得y=F(x)优于y=F(x*)，则称x*为决策空间X上的一个Pareto最优解，也称为非支配解或非受控解。一系列非受控解组成的集合称为多目标问题的Pareto解集或最佳权衡解。

2 地下水污染监测网多目标设计模型

2.1 地下水污染监测网多目标设计模型

污染物在含水层中的分布形态可以用污染羽的空间矩来刻画，即零阶矩(污染物的总质量)、一阶矩(污染羽的质心位置)和二阶矩(污染羽围绕质心的分布范围，即各个方向的协方差)［8］。三种不用的空间矩分别从不同方面来刻画污染物在空间上的分布状态。只有同时已知这三个不同的物理特征值，才能准确刻画污染羽的分布状态。假设模拟得到的污染羽浓度分布代表未来某一时刻的实际污染羽分布，亦即如果某一结点被优化模型选中，则该点位置的浓度认为已知，并由运移模型模拟所得的该点浓度值来给定。各种不同取样方案中取样点的浓度可通过插值得到一个污染羽，并分别与所有可能观测点插值计算所得到的污染羽进行比较。如果取样的点数量足够多，则插值所得到的污染羽与模拟所得到的污染羽就会趋于一致。同时，取样点数目的增加，势必增加监测费用。因此，在提高监测精度和减少监测费用两者之间必须要权衡利弊，得到最佳采样方案。数学上，地下水污染监测网多目标优化设计模型包括以下4个目标函数:(1)最小化监测费用(即取样及分析费用)；(2)最小化污染物质量评估误差；(3)最小化污染羽一阶矩评估误差；(4)最小化污染羽二阶矩评估误差。第1个目标函数表示“以最小的投入”，后3个目标函数则表示“获取最准确的污染羽空间分布信息”即污染羽的空间矩评估误差最小。具体地，优化模型可表示为:

最小化:

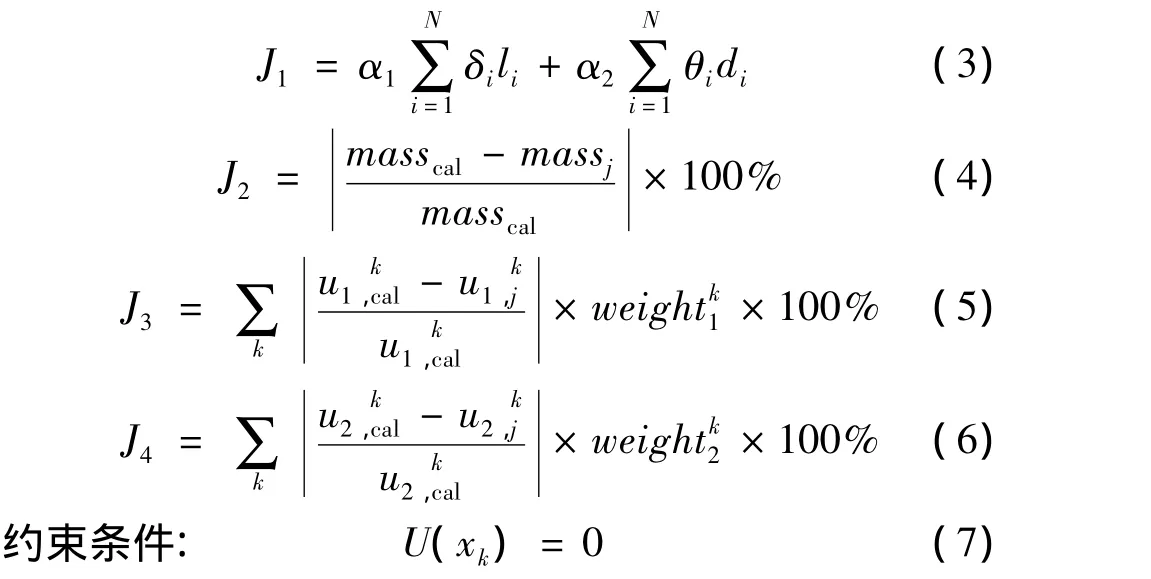
由式(3)～(7)组成的污染监测网多目标优化设计模型实际上还包含嵌入的地下水流与污染物的运移模型［10，13］。

式中:N——所有可能取样的观测井数；

α1——单个样品的采集和分析费用；

δi——二进制变量，表示在第 i号孔位置是否进行取样，如果δi=1表示取样，如果δi=0则不取样；

li——第i号孔不同深度的取样个数；

α2——第i号监测孔单位深度的安装/钻井费用；

di——第i号监测孔的深度；

θi——二进制变量，表示位置i处是否需要重新打井(即观测孔原来是否已经存在)，θi=1表示需要打井，θi=0表示观测孔已存在；

masscal——采用所有可能的观测点取样分析插值计算得到的污染物质量；

massj——采用第j个取样方案取样分析插值得到的污染物质量；

U(xk)——根据取样点数据无法插值得到污染羽未知浓度点个数。

如果某一个取样方案导致U(xk)≠0，以上4个目标函数就要受到惩罚以降低此方案的适应度值，从而保证最好的策略在进化搜索过程中得以保存下来。罚函数可表示为以下数学形式［10］:

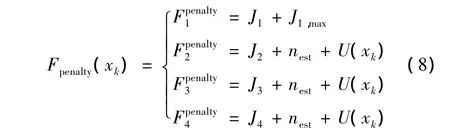
式中:nest——总的插值点数；

J1，max—— 第一个目标函数的最大值。

2.2 污染监测网多目标设计模型的求解

地下水污染监测网多目标设计模型的求解包括3个主要模块，即:地下水流和污染物运移模拟模块，污染羽空间矩评估模块，以及基于多目标进化算法的优化搜索模块。

2.2.1 地下水流和污染物运移模拟

研究采用 MODFLOW［17］和 MT3DMS［18］程序分别作为地下水流和污染物运移模型来模拟污染物在不同时段的变化状况，从而获取不同取样点位置处的真实浓度数据值。

2.2.2 污染羽空间矩评估

污染羽空间矩评估用来刻画某一特定时刻污染物的总质量以及空间分布形态。根据取样点的浓度数据值，采用普通克里格(ordinary kriging，OK)方法插值计算未知结点的浓度值［19］，得到不同方案所对应的污染羽空间分布，然后分别与采用全部取样点插值得到的污染物的总质量、一阶矩和二阶矩进行比较。进而计算和评估相应的目标函数值，并检查是否满足约束条件。

污染羽在任一时刻t关于原点的一阶矩，即污染羽质心坐标 ()可以表示为［8，20］:

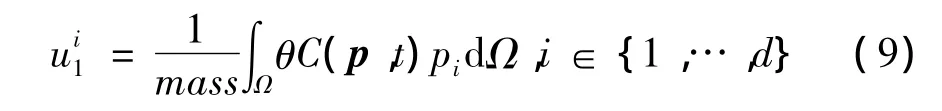
mass——污染物的总质量(零阶矩)；

C(p，t)—— t时刻污染物在空间点 p=(p1，…，pd)处的浓度；

d——空间的维数，可以是2或者3；

θ——含水层在空间点p=(p1，…，pd)处的有效孔隙度；

Ω——污染物的浓度分布区域。

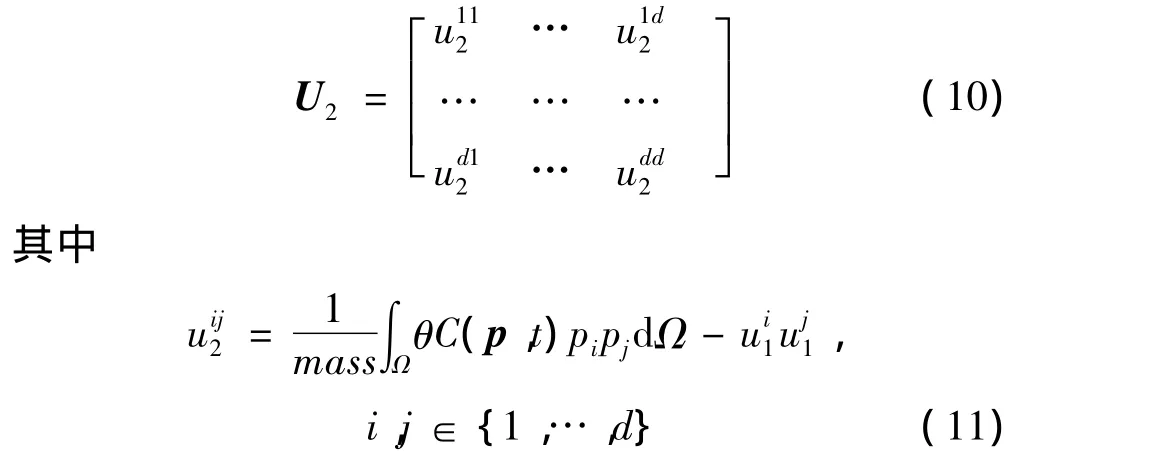
2.2.3 多目标进化求解

本次研究采用INPGA方法［15］来求解监测网多目标设计模型，其求解过程可用图1来表示。首先调用水流和溶质运移模型MODFLOW和MT3DMS获取所有可能取样点的浓度数据，根据所得到的浓度数据插值计算相应污染羽的空间矩；然后优化模型产生初始种群，并计算相应的目标函数值(监测费用、污染物质量评估误差、污染羽一阶矩评估误差、污染羽二阶矩评估误差)；经过INPGA的寻优迭代计算，最终得到地下水污染监测网多目标优化设计的Pareto最优解［7～9］。

与Erickson等［14］提到的 NPGA方法相比，INPGA方法主要通过添加Pareto解集过滤器、精英个体保留策略、邻域空间Mühlenbein变异以及个体适应值库来提高算法的搜索能力和求解效率［21～22］。

3 算例应用

3.1 场地概述

本研究算例为一均质各向同性二维承压地下水系统。如图2所示，研究区横向长600m，纵向延伸400m。已知有56个可能取样点分布于研究区(图2中的小三角形点)，假设在污染源处发生了一次泄漏(C0=1000.0×10－6mg/L)，导致地下水污染，污染羽向左边界移动。

3.2 地下水流模型和污染物运移模型

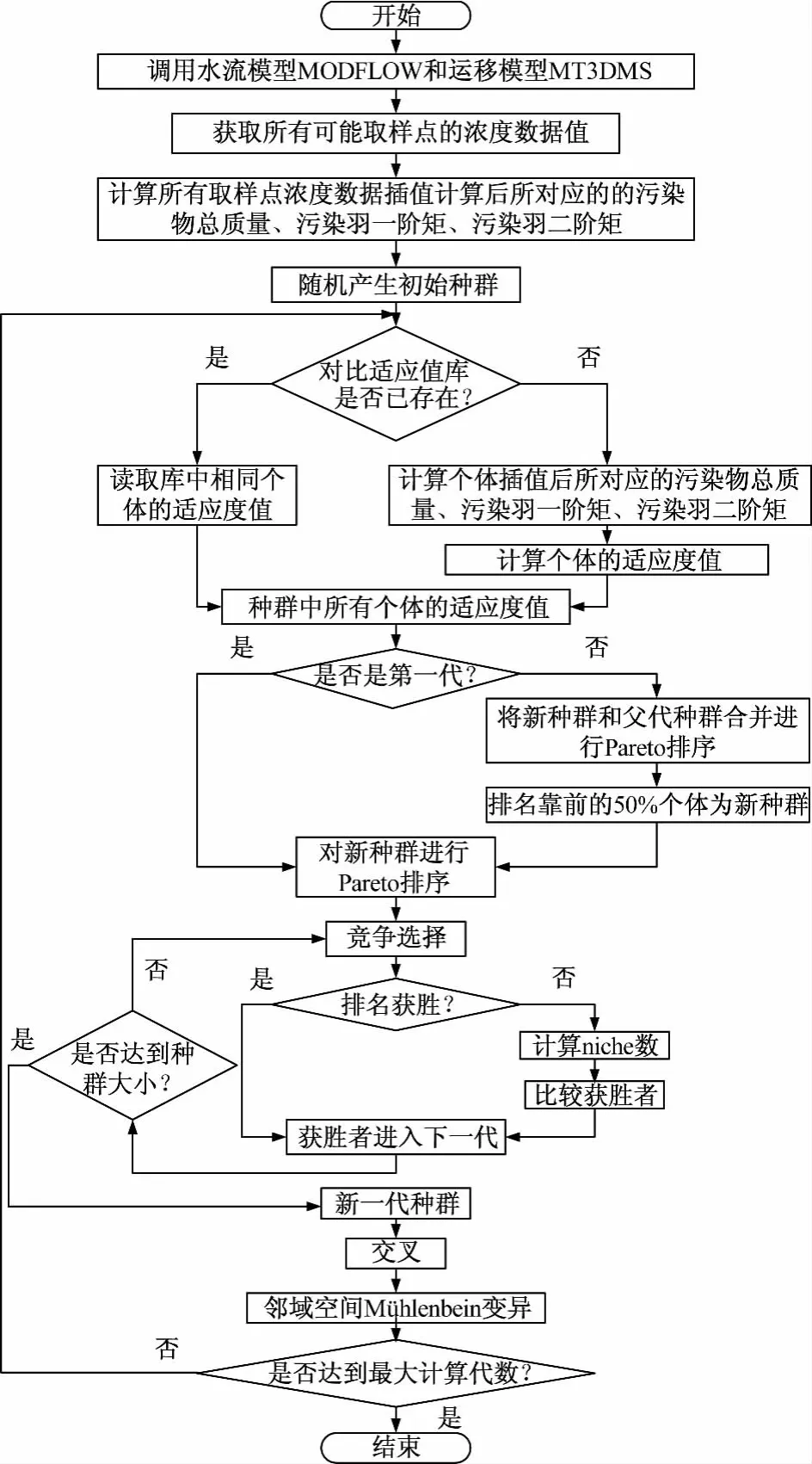
图1 地下水污染监测网多目标优化模型的进化求解流程Fig.1 Flowchart describing the evolutionary process for solving a multi-objective groundwater monitoring network design model

水流模型和污染物运移模型分别采用以有限差分法为基础的MODFLOW和MT3DMS程序进行求解。研究区空间离散为30×20=600个正方形差分网格，网格的边长为20m(图2中的浅色正方形网格)。研究区左侧边界为给定水头边界，自上而下由89.0m线性渐升为89.5m；右侧为给定流量补给边界，单位面积上的流量为9.45m/d；上下均为隔水边界。其他相关水文地质参数见表1。在此仅以污染源自泄漏起始至污染物运移3年期末作为第一个管理期来进行监测网优化设计。

3.3 监测网优化设计模型

针对此算例的监测网多目标优化设计模型可采用式(3)～(7)表示。为了方便优化模型计算，不妨定义监测费用率(即监测过程中实际取样分析费用与全部可能取样点取样分析费用之比)来代替式(3)所表示的监测费用［10］，具体可表示为:

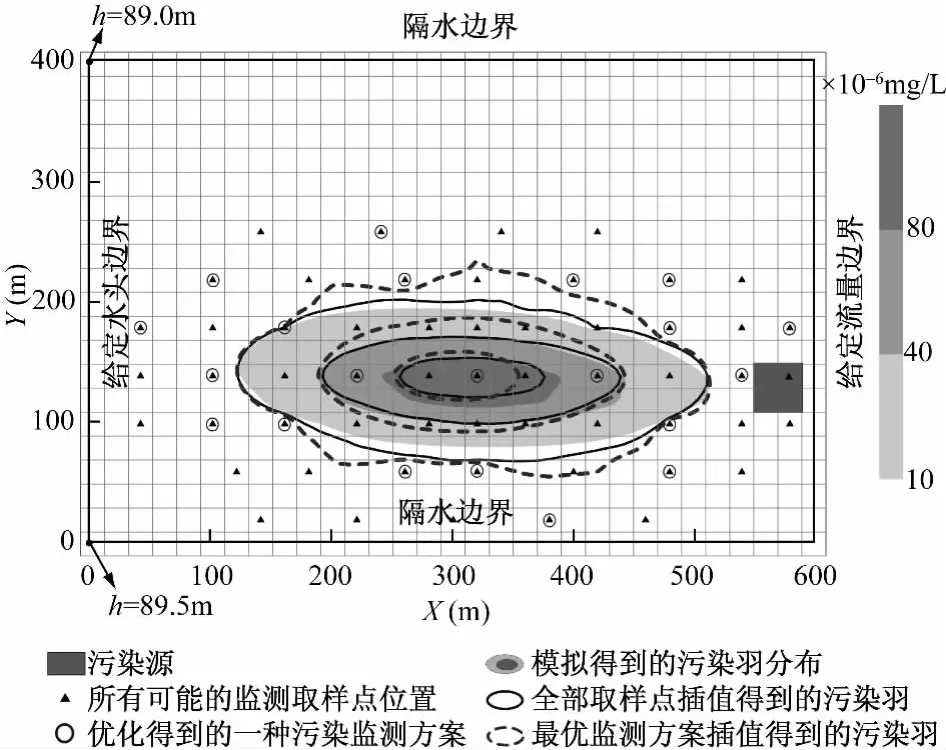
图2 研究区平面图Fig.2 Map showing the study area

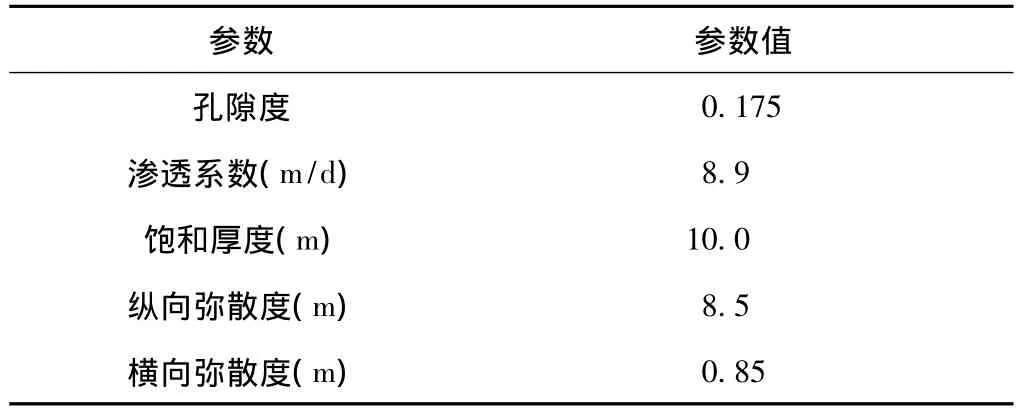
表1 算例中水流和溶质运移模型的参数(据Wu等［9］)Table 1 Parameters input to the flow and transport model［9］

其他各式保持不变。优化模型中各参数取值为:N=56；J1，max=100；nest=651；α1li和 α2di均为 2000 个货币单位；==1。

3.4 优化结果及分析讨论

在求解监测网多目标设计模型时，INPGA算法的有关参数分别取值如下:计算代数为40；种群大小为500；Pareto解集过滤器大小为400；交叉概率为0.95；Mühlenbein变异概率为0.25；小生境半径为0.05。

由INPGA优化得到的结果如图3所示。图3a为各目标函数之间的权衡关系，图3b～3d分别为图3a中优化结果在三个面上的投影，即对应3个不同目标函数之间的权衡关系。整体上，随着费用率的增加，其它3个目标函数包括质量评估误差、一阶矩和二阶矩的评估误差均呈现非线性递减的趋势，说明增加监测费用可提高污染羽的监测精度。同时，质量评估误差与一阶矩和二阶矩的评估误差均为正相关关系，尤其前两者(J2∝J3)近乎为线性正相关关系，而二阶矩评估误差受取样点数目及位置影响最为敏感。再从优化得到权衡解的空间域来看，图3中费用率的变化区间为3.57% ～66.7%，质量评估误差介于0.93%～28.25%，一阶矩评估误差和二阶矩评估误差分别介于0.86%～28.25%和6.5%～125.5%。由此说明，优化得到的权衡解的空间分布很广，可满足决策者在不同费用率(3.57%～66.7%)前提下追求监测精度最大化(J2～J4最小化)的目标。显然，当费用率超过一定程度(J1＞66.7%)时，其他各目标函数没有减小，亦即监测精度没有提高)。

图3 INPGA求解多目标模型得到的优化结果(黑边三角形点为最优解集中的一个“最优监测方案”)Fig.3 The INPGA-based optimization results showing the tradeoffs between different objectives(The black triangle indicates a preselected optimal plume monitoring design based on INPGA method)

在实际应用过程中，决策者可以根据监测费用的预算状况和污染物监测的精度需要选择图3中对应的任一特定解作为相应的监测方案。在多数情况下，决策者均需要全面权衡各个目标函数，即需要兼顾监测费用和监测精度。以图3中黑边三角形点所示的Pareto解为例(通过此监测方案得到的污染羽的浓度等值线如图2中虚线所示)，该点基本处于图中多目标解集中的拐点，其对应的费用率为37.5%，其它3个目标函数即质量评估误差、一阶矩和二阶矩评估误差分别为3.36%，2.86%和20.17%。在费用率J1＜37.5%时，随着费用率的增加，污染羽监测精度也能明显得到提升；而在费用率J1＞37.5%时，监测精度之提升速率随着费用率的增加明显减缓。因此，在需要兼顾监测费用和监测精度的情况下，一般说来，决策者可将此三角形点对应的解作为污染监测实施过程中的监测方案。

在有些情况下，根据场地实际和污染物性质，如果污染物对环境危害不太大，公众反应也不太敏感，这时可能更关注节省监测费用，决策者可根据费用预算情况选择最能刻画污染羽空间分布的Pareto解作为监测方案。而另外有些情况，如污染物的毒性很强，同时对公众影响巨大，这时最关注的应该是监测精度，而不会过分强调节省监测费用，决策者则需选择监测精度尽可能高的Pareto解作为监测方案。

由以上不同情况可知，利用多目标模型进行地下水监测网优化设计，由INPGA求解一次多目标模型就可得到一系列权衡解，决策者具有充分的选择权，可根据实际情况选择不同的权衡解作为相应的监测方案。这是多目标优化模型的最显著优势。与此相反，如果不采用多目标优化模型求解上述监测网优化问题，则需要将以上多目标模型转化为单目标模型，即保留1个目标函数，其它3个目标函数变为给定阈值的相应约束条件，利用单目标遗传算法即可求解。但这种情况下，约束条件下的右端项具有较大的人为性和主观性，依赖于分析者的个人专业经验，同时利用单目标遗传算法每运行一次单目标模型只能得到依赖于约束条件右端项的一个解，决策者没有其它选择，会有“分析者取代决策者之嫌”。

4 结论

(1)本文采用模拟-优化方法建立了一个包括监测费用、污染物质量评估误差、污染羽一阶矩和二阶矩评估误差等4个目标函数的地下水污染监测网设计的多目标优化模型。同时，采用进化算法求解，可得到能真实反映各个目标函数之权衡关系的一系列Pareto权衡解，而不用考虑惩罚因子的影响。

(2)污染羽质量评估误差与一阶矩评估误差和二阶矩评估误差均为正相关关系。同时，二阶矩评估误差对取样点数目及其位置最为敏感，表明污染羽外围监测点对准确刻画污染羽的空间分布具有重要作用。

(3)采用多目标模型进行地下水污染监测网优化设计，能最大限度地减少分析者的主观性，同时，利用进化算法求解多目标模型，一次求解就能获得一系列权衡解集，其设计效率高，能给决策者以充分的选择权。

［1］吴剑锋，黄昌硕.Delaunay方法的改进及其在地下水污染监测网设计中的应用［J］.水科学进展，2006，17(3):305－311.［WU J F，HUANG C S.Improvement of Delaunay method and its application to spatial sampling network design for contaminant plume monitoring［J］.Advance in Water Science，2006，17(3):305－311.(in Chinese)］

［2］Loaiciga H A.An optimization approach for groundwater quality monitoring network design［J］.Water Resources Research，1989，25(8):1771－1780.

［3］周磊，王翊红，林健，等.北京平原区地下水水质监测网优化设计［J］.水文地质工程地质，2008，35(2):1－9.［ZHOU L，WANG Y H，LIN J，et al.Optimal design of monitoring network of groundwater quality in the Beijing Plain［J］.Hydrogeology ＆Engineering Geology，2008，35(2):1 － 9.(in Chinese)］

［4］高赞东，段秀铭，王庆兵，等.济南岩溶泉域地下水水质监测［J］.水文地质工程地质，2008，35(2):10－17.［GAO Z D，DUAN X M，WANG Q B，et al.Groundwater quality monitoring in the Jinan karstic spring basin［J］.Hydrogeology＆ Engineering Geology，2008，35(2):10－17.(in Chinese)］

［5］郭占荣，刘志明，朱延华.克立格法在地下水观测网优化设计中的应用［J］.地球学报，1998，19(4):429－433.［GUO Z R，LIU Z M，ZHU Y H.The application of kriging estimation to the optimal design of groundwater observation network ［J］.Acta Geoscientica Sinica，1998，19(4):429 － 443.(in Chinese)］

［6］Wagner B J.Sampling design methods for groundwater modeling under uncertainty［J］.Water Resources Research，1995，31(10):2581－2591.

［7］Reed P M，Minsker B S，Valocchi A J.Costeffective long-term groundwater monitoring design using a genetic algorithm and global mass interpolation［J］.Water Resources Research，2000，36(12):3731－3741.

［8］Wu J F，Zheng C M，Chien C C.Cost-effective sampling network design for contaminant plume monitoring under general hydrogeological conditions［J］.Contaminant Hydrology，2005，77:41－65.

［9］Wu J F，Zheng C M，Chien C C， et al.A comparative study of Monte Carlo simple genetic algorithm and noisy genetic algorithm for cost-effective sampling network design under uncertainty ［J］.Advances in Water Resource，2006，29:899 －911.

［10］Kollat J B，Reed P M.Comparing state-of-the-art evolutionary multi-objective algorithms for long-term groundwater monitoring design ［J］.Advances in Water Resource，2006，29:792－807.

［11］吴剑锋，郑春苗.地下水污染监测网的设计研究进展［J］.地球科学进展，2004，19(3):429－ 436.［WU J F，ZHENG C M.Contaminant monitoring network design:recent advances and future directions［J］.Advance in Earth Sciences，2004，19(3):429－436.(in Chinese)］

［12］彭伟，吴剑锋，吴吉春.NPGA-GW在地下水系统多目标优化管理中的应用［J］.高校地质学报，2008，14(4):631－636.［PENG W，WU J F，WU J C.Application of Niched Pareto genetic algorithm to multi-objective optimal design of groundwater system［J］.Geological Journal of China Universities，2008，14(4):631－636.(in Chinese)］

［13］Ritzel B J，Eheart J W，Ranjithan S.Using genetic algorithms to solve a multiple objective groundwater pollution containment problem［J］.Water Resources Research，1994，30(5):1589－1604.

［14］Erickson M，Mayer A，Horn J.Multi-objective optimal design of groundwater remediation systems:application of the niched Pareto genetic algorithm(NPGA)［J］.Advances in Water Resources，2002，25(1):51－65.

［15］吴剑锋，彭伟，钱家忠，等.基于INPGA的地下水污染治理多目标优化管理模型:I-理论方法与算例验证［J］.地质论评，2011，57(2):277－284.［WU J F，PENG W，QIAN J Z，et al.INPGA-based multi-objective management model for optimal design of groundwater remediation system:I.methodology and its experimental validation ［J］. Geological Review，2011，57(2):277－284.(in Chinese)］

［16］吴剑锋，彭伟，钱家忠，等.基于INPGA的地下水污染治理多目标优化管理模型:II-实例应用［J］.地质论评，2011，57(3):437－443.［WU J F，PENG W，QIAN J Z，et al.INPGA-based multiobjective management model for optimal design of groundwater remediation system:II.application to the MMR Site［J］.Geological Review，2011，57(3):437 －443.(in Chinese)］

［17］Harbaugh A W，McDonald M G.Programmer＇s Documentation for MODFLOW-96，An Update to The U.S.Geological Survey Modular Finite-difference Ground-water Flow Model［R］.U.S.Geological Survey Open-File Report 96-486，1996:220.

［18］Zheng C M，Wang P P.MT3DMS:A Modular Three-dimensional Multi-species Transport Model for Simulation of Advection，Dispersion and Chemical Reactions of Contaminants in Groundwater Systems；Documentation and User’s Guide，Contract Report SERDP-99-1［R］.Vicksburg:U S Army Engineer Research and Development Center，1999.

［19］Deutsch CV，Journal AG.GSLIB:Geostatistical Software Library and User’s Guide［M］.2ndEd.New York:Oxford University Press，1998.

［20］阎婷婷，吴剑锋.渗透系数的空间变异性对污染物运移的影响研究［J］，水科学进展，2006，17(1):29－36.［YAN T T，WU J F.Impacts of the spatial variation of hydraulic conductivity on the transport fate of contaminant plume［J］.Advances in Water Science，2006，17(1):29－36(in Chinese)］

［21］Deb K，Pratap A，Agarwal S，Meyarivan T.A Fast and Elitist Multi-Objective Genetic Algorithm:NSGAII［J］.Evolutionary Computation，2002，6(2):182－197.

［22］Herrera F，Lozano M，Verdegay J L.Tackling realcoded genetic algorithm:operators and tools for behavioural analysis ［J］. Artificial Intelligence Review，1998，12(4):265－319.