三次NURBS曲线插值在土工织物有效孔径分析中的应用

王 宵

（上海勘测设计研究院 上海 200434)

1 引言

土工织物的有效孔径是土工织物排水反滤的一个重要指标，直接反映织物的保土能力和排水能力。有效孔径的测试方法主要有筛析法（干筛法、湿筛法、动力水筛法)、显微镜测读法、气泡点法等。由于筛析法最能模拟颗粒通过土工织物的工程实际情况，且干筛法最为简便，因此我国目前在对于土工织物的有效孔径检测试验中，主要采用干筛法。有效孔径以能有效通过土工织物的近似最大颗粒直径表示，例如O90表示土工织物中90%的孔径低于该值。此外常用的表示方式还有O95和O98等。

干筛法有效孔径的测试原理是：用土工织物作为筛布，将已知直径的标准颗粒放在土工织物上面振筛，称量通过土工布的标准颗粒材料重量，计算出过筛率，以该过筛率和标准颗粒直径为一组数据，调换不同直径的标准颗粒进行试验，得出至少三组数据，由此绘出土工织物的孔径分布曲线。然后在曲线上得出O90、O95以及O98。

传统的有效孔径试验数据处理，是将试验获得的数据，在半对数坐标纸上标出，然后将数据点用曲线板手绘连成曲线，得到一条织物有效孔径的分布曲线，然后再从曲线上查取 O90、O95以及O98值，这种手绘的数据处理方法不仅繁琐，而且不可能得到连续光滑的曲线，局部总是存在奇异点，大大降低了实验数据的准确度。通过对多种样条插值函数数学原理的分析比较，采用三次非均匀有理B样条曲线（NURBS曲线)对土工织物有效孔径的实验数据进行插值，能很好的解决有效孔径试验数据处理，并且便于使用计算机语言开发计算及绘图程序，大大提高土工织物有效孔径数据处理的效率和精度。

2 土工织物有效孔径分布曲线的特点

2.1 曲线的连续性

根据国标《土工布及其有关产品有效孔径的测定干筛法》（GB/T14799-2005)中土工织物有效孔径分布曲线的定义，曲线的纵坐标为一块织物中大于某一粒径的孔径的百分比，为累积型曲线，不可能出现断点，因此曲线必定是连续的。

2.2 曲线的光滑性

在生产条件不变的情况下，生产出来的土工织物的孔径大小符合正态分布，这一点已经得到共识，其概率分布如图1所示。

正态分布的概率密度函数为：

分布函数为：

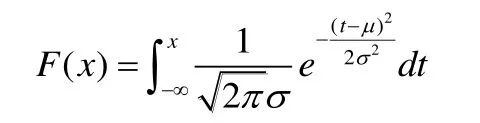
正态分布函数为e为底的指数型函数，具有n阶连续导数，因此土工织物的孔径分布曲线必定是光滑的，至少具有一阶连续的导数，理论分布曲线如图2所示。

图1 织物孔径概率分布曲线

图2 织物孔径理论分布曲线

2.3 曲线的单调性

孔径分布曲线为累积性曲线，孔径大的点对应的筛余量不可能大于孔径小的点，所以曲线按照坐标轴的排列不同，一定是单调递增或是递减。

3 插值方法的比较及数学原理

根据对土工织物有效孔径累积分布曲线的特点分析，对于曲线的要求是根据数据点绘出的孔径分布曲线必须是经过型值点(即数据点)的光滑的（至少具有一阶连续导数)连续的单调的曲线。

插值的定义：给定一组精确的数值点，要求构造一个函数，使之严格地依次通过全部型值点，且满足光滑的要求。

插值的方法：

（1)多项式插值：这是最常见的一种函数插值，已知平面上n＋1个不同点，要寻找一条n次多项式曲线通过这些点。插值多项式一般有拉格朗日插值多项式和牛顿插值多项式两种常见的表达形式。多项式插值有阶数低，易出现奇异点的明显缺点；

（2)三次均匀样条插值：采用分段 3次多项式作为插值函数，数据点间距较大时出现曲线奇异；

（3)三次非均匀有理 B样条插值：也称作三次NURBS曲线，是目前使用最为广泛，最好的样条插值曲线，它具有连续的二阶导数和光滑的插值曲线，且克服了均匀样条插值函数节点间距较大时产生的曲线奇异。

非均匀有理B样条曲线（NURBS曲线)由节点向量、控制点、权值唯一确定。一条k次非均匀有理B样条曲线的定义为：

式中：wi(0≤i≤n)为控制权因子；vi(0≤i≤n)为控制顶点；Ni,k(u)是由节点矢量

U=[u0,u1,.......un+k+1]决定的k次规范B样条基函数，由de-Boor-Cox递推公式定义：

并规定0/0＝0。

4 三次NURBS插值函数的确定

4.1 三次NURBS插值函数的矩阵表达式

根据递推公式可以得到三次NURBS插值函数的矩阵表达式：

（1≤i≤n-1，n为型值点个数)

其中 t=(u-ui)/(ui+1-u)(0≤t≤1)，Ni为由节点向量确定的4阶矩阵。

B样条曲线是由控制顶点连线构成的控制多边形确定，一般不通过控制多边形的控制顶点，因此需要根据型值点（数据点) pi(1 ≤i ≤n)反求控制顶点 vi( 0≤i ≤n+1)。根据型值点条件以及边界条件可得到n+2个方程，即由n个型值点可以唯一确定n+2个控制点。边界条件可以由曲线两端的一阶导数 pi(t)′或是两阶导数pi( t)′确定。根据实际情况在这里选用第二类边界条件，可取 p1(0 )′=0,pn-1(1)′=0。

4.2 节点向量的确定

三次样条插值函数的均匀与非均匀性质的主要区别在于节点向量的取值。干筛法有效孔径的数据点之间的间距一般变化较大，数据点分布不均匀，在此选用弦长累积法确定节点向量。

通过n个型值点三次样条插值函数的节点向量可以表示为：

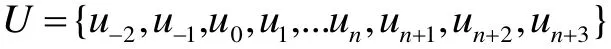
其中（n≥3)。

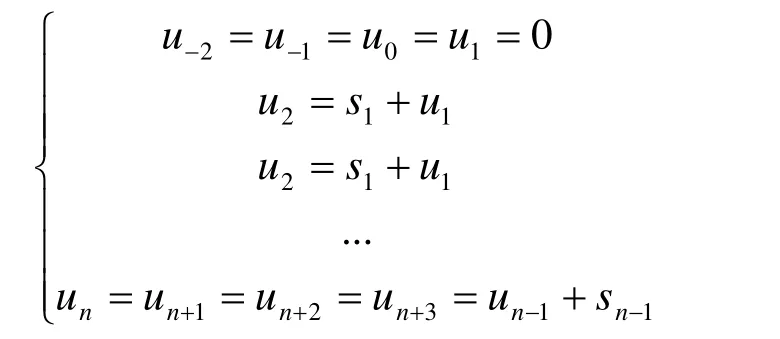
5 应用三次NURBS插值函数绘制孔径分布曲线的VC++语言实现

按照国标《土工布及其有关产品有效孔径的测定干筛法》（GB/T14799-2005)，确定某一试样的有效孔径，需要取得不少于三组连续分级标准颗粒材料的过筛率，每组粒径需要取得5块试样的平均值。根据经验，实际的试验过程中，要取得完整的4组粒径的筛余量是比较困难的。因为对于织物孔径分布而言，4组粒径范围过大，容易出现最小粒径筛余率为0g，或是最大的粒径筛余率为50g的情况，这两种数据都是无效的数据。对于仅需要得到以O90、O95以及O98为代表的织物有效孔径而言，只要保证所求的有效孔径落在孔径曲线的第一段内，那么第四个数据点对曲线第一段的形状基本没有影响，即不会影响有效孔径的数值。所以实际试验中一般选用3组粒径，即满足了规范和数据准确性的要求，又简化了实验过程。基于以上对土工织物有效孔径实验的数据点及孔径分布曲线特性的分析，编制采用通过3个数据点的三次非均匀有理B样条插值函数来绘制土工织物孔径分布曲线的程序，是解决土工织物有效孔径实验数据处理的最好方法。

程序采用 VC++语言实现，设计流程如图 3所示：

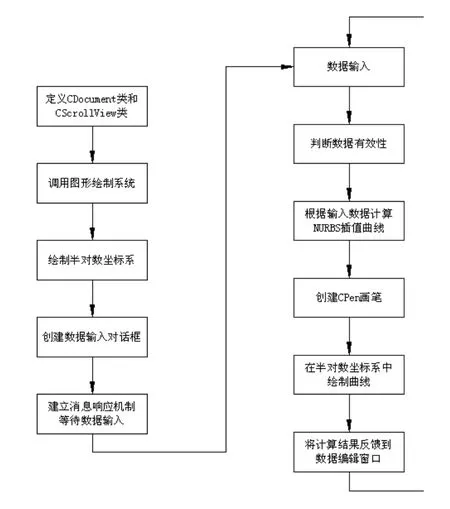
图3 孔径分布曲线程序的流程图

6 孔径曲线的修正

土工织物按照加工的方式分为有纺和无纺两种，当织物中的孔隙较集中地分布在一个小范围内时，用筛析法测试土工织物的孔径，往往会出现两组连续颗粒粒径间筛余率相差很大的情况。这种情况较多出现在一些较厚的无纺布当中，这样得到的两个数据点之间间距较大，很容易出现不单调的情况，这显然是不合理的。

产生曲线不单调的原因在于两数据点间距太大，这一段曲线因为缺少必要的数据点，为满足边界条件曲线会出现不单调递增，解决方法有两种：一是在两数据点之间添加新的数据点，但是由于规范已经规定好了标准颗粒的粒径范围，同时相邻粒径之间相差已经很小，再细化可能标准颗粒粒径本身误差就会很大，因此实施起来比较困难；二是根据情况加大首端或末端型值点的权值，根据首末端曲线的弯曲程度可以建立起曲线首末端斜率k与权值w的对应函数关系，这样曲线出现不单调时，就可以通过自动调节首末端点的权值大小来修正实际孔径曲线的单调性。

7 工程实例

表1 无纺布规格参数

表2 无纺布有效孔径实验数据

我们选取了一组典型的厚度较大的无纺土工布，规格如表 1所示。按规范规定的粒径组（0.071～0.090，0.090～0.125，0.125～0.154，分别取粒径范围下限)取得3组数据。因为实际取得的0.071和0.090两组粒径对应的数据点之间间距较大，将0.071～0.090之间的砂重新过0.075mm的筛网，取得 0.075～0.090粒径范围的砂，额外增加了0.075粒径对应的一组数据点。因此一共取得了4组数据，如表2所示。然后在半对数坐标内，分别用三次均匀样条插值函数和三次非均匀有理B样条插值函数绘制3个数据点和4个数据点的孔径分布曲线，如图4、5、6、7所示。

图4 3个数据点经过三次均匀样条插值得到的孔径分布曲线

经过图中的对比可以看出当数据点间距较大时，三次均匀样条曲线当3个数据点分布不均匀时，很容易出现曲线奇异，而未经修正的三次非均匀有理 B样条曲线很好的解决了数据点分布不均匀时出现的曲线奇异，但是数据点间距较大时，单调性容易发生改变，应用在实际的有效孔径测试中，这肯定是不合理的。经过权值修正后曲线的单调性得到了很好的控制，并且与新增数据点后得到的实际的孔径分布曲线基本一致，很好的拟合了实际的孔径分布曲线。

图5 3个数据点经过三次非均匀有理B样插值得到的孔径分布曲线

图6 4个数据点经过三次非均匀有理B样条插值得到的孔径分布曲线

图7 3个数据点经权值修正后的孔径分布曲线

8 结语

采用通过型值点的三次非均匀有理 B样条插值函数，对土工织物干筛法有效孔径实验数据进行了插值，并绘制了连续光滑的孔径分布曲线。此外对曲线绘制中可能出现的的不单调性，提出了权值修正方法，进行了曲线修正，在此基础上开发了土工织物有效孔径分布曲线绘制程序。这一方法解决了长期以来用曲线板手工绘制孔径分布曲线，然后再从曲线上查取有效孔径数值的非常繁琐、且误差较大的数据处理方法，大大地提高了土工织物有效孔径数据处理和绘制分布曲线的效率和精度。