基于Copula理论的风光互补发电系统可靠性评估

赵继超 ，袁 越 ，傅质馨 ，孙纯军 ，钱 康 ，许文超

（1.河海大学 能源与电气学院，江苏 南京 211100；2.河海大学 可再生能源发电技术教育部工程研究中心，江苏 南京 210098；3.江苏省电力设计院，江苏 南京 211102）

0 引言

随着可再生能源发电设备制造工艺的不断革新以及可再生能源并网技术的持续快速发展，风力发电、光伏发电已经成为当前可再生能源利用的2种主要形式。然而，由于风速、光照强度等自然因素固有的随机性和波动性，风电场、光伏电站的出力呈现较强的间歇性和不可控性。随着间歇性电源穿透功率的增加，可再生能源并网给电力系统带来的影响日益突出，严重影响电力系统的安全、稳定、可靠运行。因此，对含可再生能源的发电系统进行准确的可靠性评估十分必要。

上述问题的关键在于建立准确的可再生能源发电系统可靠性模型，主要方法有解析法［1-2］和蒙特卡罗模拟法［3-4］。针对多个风电场之间出力的相关性研究，文献［5］通过蒙特卡罗模拟法产生2组无相关特性的风速向量，采用矩阵变换技术模拟风电场之间的关联特性；文献［6］采用ARMA时间序列法得到具有时序特性的风速序列，在此基础上应用遗传算法产生2组具有关联特性的风速序列。文献［7-8］在进行风光混合发电系统的可靠性评估时，认为风电、光伏的出力是相互独立的，并未计及风电、光伏出力的相关性。然而，同一地区的风电、光伏出力往往具有互补性，即负相关特性。两者之间的相关性会改变风光互补发电系统出力的概率分布，影响发电系统的可靠性评估。目前，关于风电场、光伏电站出力相关性的研究尚未见到报道。为了考虑同一地区风电场、光伏电站出力的相关性，本文提出一种应用Copula理论建立风光互补发电系统可靠性模型的新方法。

Copula理论可以将1个联合分布分解为k个边缘分布和1个Copula函数，Copula函数描述了变量间的相关性［9］。文献［10］应用该理论计算了冰风暴灾害下电力断线倒塔的概率。文献［11］采用Copula理论，描述了多个可再生分布式电源出力的统计特性。文献［12］基于Copula理论，研究了上海地区台风条件风速和雨强联合概率分布。

本文通过江苏沿海某风光互补电站示范工程的实测数据，采用核密度估计的方法，得到风电场、光伏电站出力的概率分布；选取Kendall秩相关系数度量两者之间的相关程度；基于Copula理论，建立风光互补电站的可靠性模型；以RBTS标准测试系统作为算例，采用该模型对风光互补发电系统进行可靠性评估。

1 风电场和光伏电站出力的概率分布

建立风电场、光伏电站出力的概率模型，常采用参数估计法，假定风速服从Weibull分布、光照强度短时服从Beta分布，通过估计其中的参数获取概率分布。然而，参数估计法的结果不能总令人满意，原因在于选取的参数模型与实际的物理模型之间往往存在较大的差距；风电场、光伏电站的出力不仅取决于风速、光照强度，而且还受其他诸多因素的影响，如风电场风机的布局、光伏面板的倾角等。因此，本文根据江苏沿海某风光互补电站示范工程的实测数据，采用非参数核密度估计法，获取风电、光伏出力的概率分布。

1.1 核密度估计

核密度估计属于非参数检验方法之一，该方法不需要分布的先验知识和任何概率分布形式的假设，是一种从数据样本本身出发，研究数据分布特征的方法［13］。

设 x1、x2、…、xn为随机变量 x 的样本，令随机变量 x 的概率密度函数为 f（x），则 f（x）的核密度估计为［14］：

其中，n为样本容量；h为平滑系数；K（·）为核函数，通常选取以0为中心的对称单峰概率密度函数。

常用的核函数以及核函数的基本性质参考文献［14］。 数学理论证明，fh（x）将继承核函数 K（·）的连续性和可微性，若选用高斯核函数，则fh（x）可以进行任意阶微分［13］。

1.2 风电场和光伏电站出力的概率分布

将实测的出力数据折算成出力率，进行归一化处理，选取风电场、光伏电站的出力率为随机变量。

设风电场的出力率为P1，其对应的概率密度为fWT（P1）；光伏电站的出力率为 P2，其对应的概率密度为 fPV（P2）。 令（p11，p12，…，p1n）和（p21，p22，…，p2n）分别为P1和P2的样本空间，n为样本容量。

分别将（p11，p12，…，p1n）和（p21，p22，…，p2n）代入式（1），可估计出 fWT（P1）和 fPV（P2）。 核密度估计图与实测数据的频率直方图对比见图1和图2。

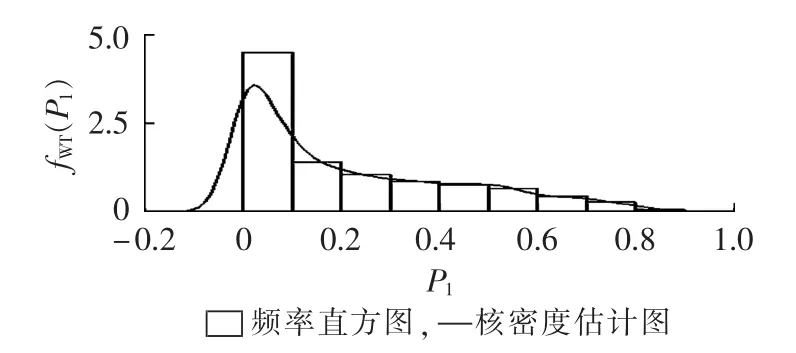
图1 风电场出力的概率密度曲线Fig.1 Probability density curve of wind farm output

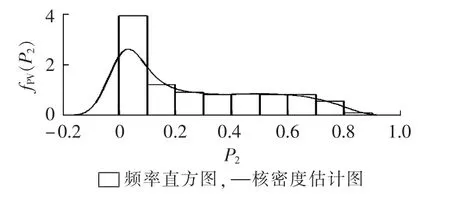
图2 光伏电站出力的概率密度曲线Fig.2 Probability density curve of PV station output

分别对 fWT（P1）和 fPV（P2）进行积分运算，可得风电场和光伏电站出力的累积概率分布 FWT（P1）和FPV（P2），计算公式如下：

经核密度估计的累积概率分布曲线与实测数据的经验分布对比见图3。

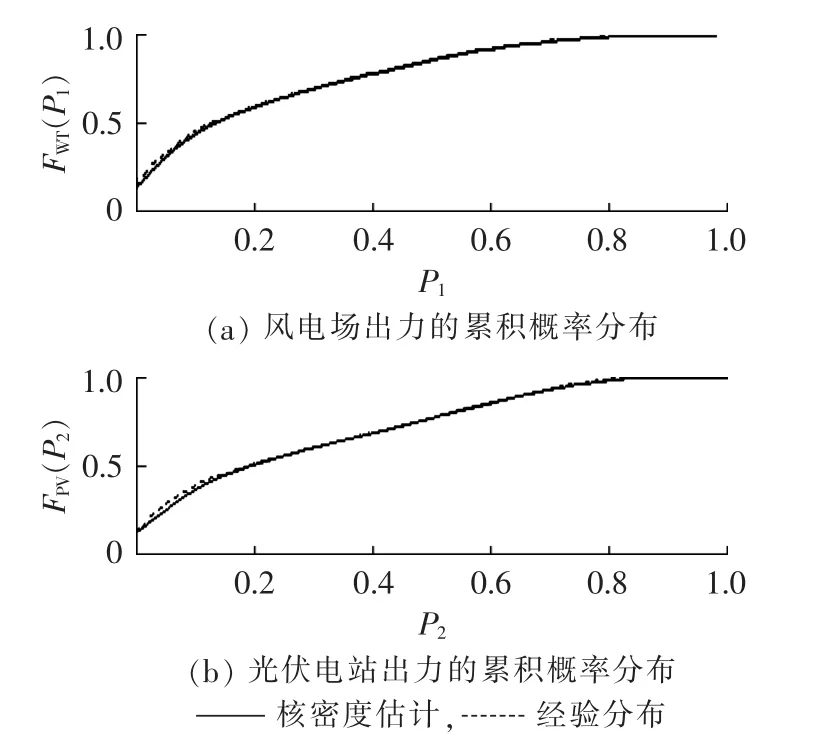
图3 累积概率分布曲线Fig.3 Cumulative probability distribution curve

由图1和图2可以看出，采用核密度估计法得到的概率密度曲线与频率统计直方图基本吻合，但概率密度函数的支撑集超出了出力率［0，1］范围，这是由核密度估计算法的边界效应造成的。由图3可以看出，采用核密度估计法得到的累积概率分布函数曲线与经验分布基本一致，因此，可以忽略密度函数支撑集溢出对风电场、光伏电站出力概率分布的影响。

2 Copula理论与相关性分析

2.1 Copula函数的定义

风电场、光伏电站的出力存在互补性，且非线性相关，通过传统的概率理论确定两者的联合概率分布计算复杂。Copula理论的提出，为解决复杂高维联合分布问题提供了一种新思路。它将联合分布问题转化为边际分布和相关程度2个问题，模型实用、有效，简化了计算。

假设 H（·，·）为具有边缘分布 F（·）和 G（·）的联合分布函数，那么存在一个Copula函数C（·，·），满足［9］：

此外，通过 Copula函数 C（·，·）的密度函数c（·，·）和边缘分布函数 F（·）、G（·），可以求出分布函数 H（·，·）的密度函数：

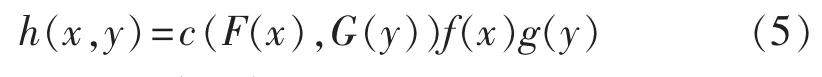
在Copula函数族中，阿基米德Copula性质优良，应用广泛。Gumbel、Clayton和Frank Copula函数是3类常用的二元阿基米德Copula函数。其中Gumbel Copula和Clayton Copula函数只能描述变量间的非负相关关系，而Frank Copula函数还可以描述变量间的负相关关系。

考虑到同一地区的风电场、光伏电站的出力往往具有互补性，即负相关特性，本文选取Frank Copula函数作为风电场、光伏电站出力联合概率分布的连接函数。Frank Copula函数的分布函数和密度函数分别为：

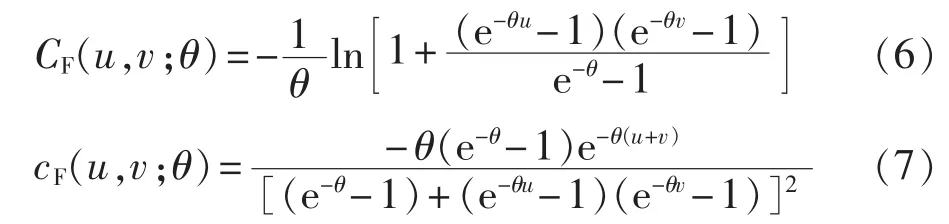
其中，θ为相关参数，θ≠0，θ＞0 表示随机变量 u、v正相关，表示随机变量u、v趋向于独立，θ＜0表示随机变量u、v负相关。

2.2 Copula函数的相关性测度

Pearson线性相关系数是目前常用的处理2个随机变量相关性问题的方法，如文献［6］度量2个风电场风速的相关性。然而，利用Pearson线性相关系数处理非线性相关性问题时存在如下缺陷：

a.若随机变量的概率分布具有厚尾特性，Pearson线性相关系数不能准确描述变量间的相关性；

b.在进行非线性变换过程后，变换前后变量间的相关程度发生变化；

c.随机变量间存在相关关系，但Pearson线性相关系数可能为零。

由于Kendall秩相关系数和Spearman秩相关系数在Copula理论中要优于Pearson线性相关系数［11］，因此本文采用Kendall秩相关系数来度量风电场、光伏电站出力的相关性。

设集合 φ＝｛（x1，y1），（x2，y2），…，（xN，yN）｝为由随机向量（X，Y）的N组观测值组成的样本空间，其中X和Y均为连续的随机变量，且xi和yi在时间上一一对应。 令（xi，yi）和（xj，yj）为从 φ 中随机选取的 2 组观测值，i，j=1，2，…，N 且 i≠j，如果 xi＜xj且 yi＜ yj，或者 xi＞xj且 yi＞yj，即（xi-xj）（yi-yj）＞0，则称（xi，yi）和（xj，yj）是一致的；类似地，如果（xi-xj）（yi-yj）＜0，则称（xi，yi）和（xj，yj）是不一致的。

Kendall秩相关系数表示从样本中随机选取的观测值（xi，yi）和（xj，yj），i≠j，一致的概率与不一致的概率之差。由此可得Kendall秩相关系数定义的一般形式。

令（xi，yi）和（xj，yj）为随机向量（X，Y）的任意 2 个可能值，那么（xi，yi）和（xj，yj）独立同分布，定义

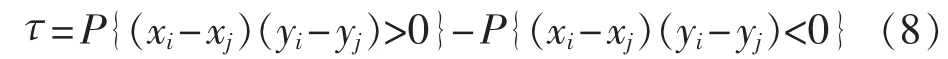
为Kendall秩相关系数，记为τ∈［-1，1］，i≠j。式中P表示事件发生的概率。

若τ＞0，随机变量 X、Y 正相关；若τ＜0，随机变量X、Y负相关；若τ=0，不能确定随机变量X、Y的相关关系。

Kendall秩相关系数τ与Frank Copula函数中相关参数θ的关系为：

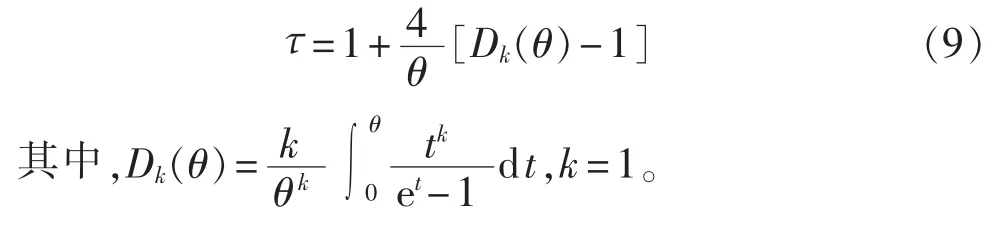
3 风光互补发电系统的可靠性模型

3.1 风光互补发电系统出力的概率分布

风光互补发电系统的出力为互补电站中风电场和光伏电站出力之和。求取风光互补发电系统出力的概率分布可以转化为求取互补电站中风电场、光伏电站出力的联合概率分布。

令随机变量P1和P2分别为风电场和光伏电站的出力率，（p11，p12，…，p1n）和（p21，p22，…，p2n）分别为随机变量P1和P2的样本空间，n为样本容量，且p1i和 p2i在时间上一一对应，那么（p1i，p2i）和（p1j，p2j）为独立同分布的随机向量，其中 i，j=1，2，…，n 且 i≠j。

根据Copula理论，风光互补发电系统中风电场、光伏电站出力的联合概率分布可由如下步骤计算：

a.根据样本（p11，p12，…，p1n）和（p21，p22，…，p2n），利用式（1）进行核密度估计得到 fWT（P1）和 fPV（P2）；

b.将 fWT（P1）和 fPV（P2）分别代入式（2）和（3），计算风电场和光伏电站出力的累积概率分布FWT（P1）和 FPV（P2）；

c.将（p1i，p2i）和（p1j，p2j）代入式（8），计算风电场和光伏电站出力的Kendall秩相关系数τ；

d.将τ代入式（9），计算Frank Copula函数相关参数θ；

e.将式（5）和式（7）联立，得到随机变量 P1和 P2的联合概率密度。

其数学表达式为：

其中，u=FWT（P1），v=FPV（P2），θ为步骤 d 确定的 Frank Copula函数的相关参数。

经计算，该风光互补示范工程中风电场、光伏电站出力的Kendall秩相关系数τ=-0.161，两者的联合概率密度如图4所示，风电场、光伏电站出力的频数统计直方图见图5，实际统计的详细数据见表1。由图4和图5可以看出，基于Copula理论所建立的风电场、光伏电站出力的联合概率密度模型，较好地刻画了风光互补电站出力的统计特性。

3.2 风光互补发电系统的可靠性模型

为了突出问题，本文在建立风光互补发电系统的可靠性模型时，重点考虑风电场、光伏电站出力的随机性与两者之间的相关性，暂不考虑风光互补发电系统的元件故障特性，认为风光互补发电系统元件完全可靠。

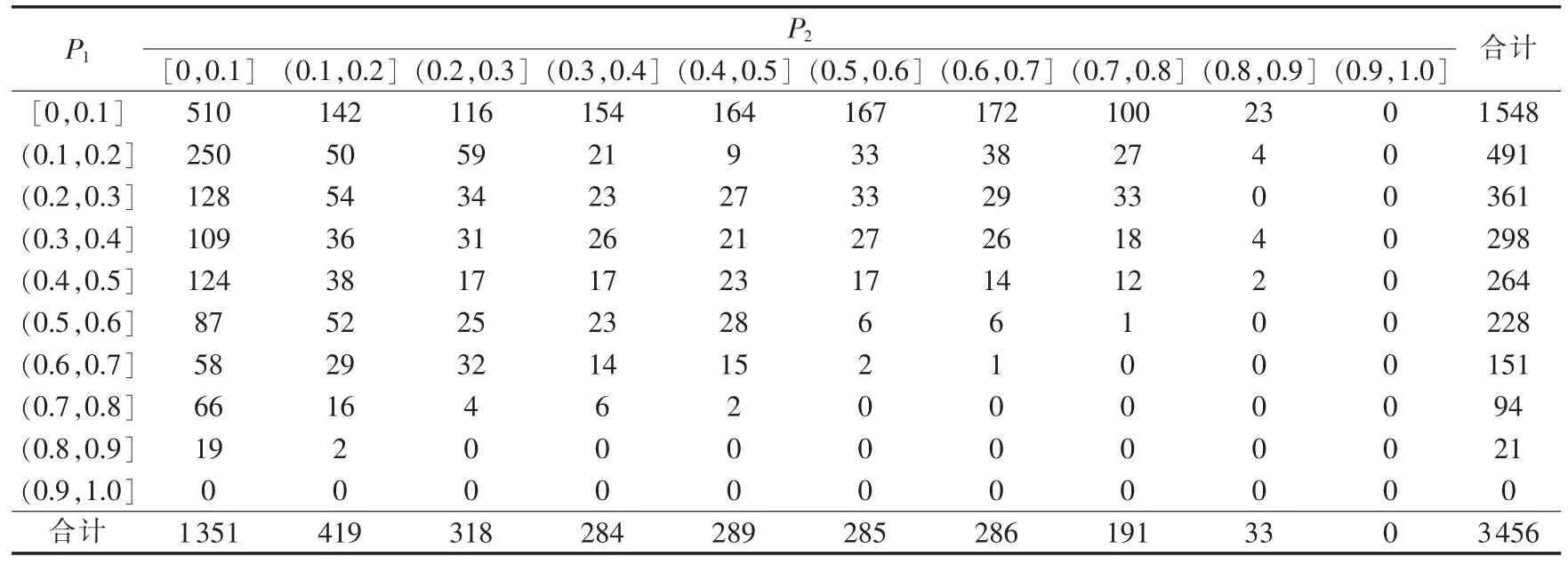
表1 风电场和光伏电站实测出力的统计结果Tab.1 Statistics of measured power outputs of wind farm and PV station

图4 风电场和光伏电站出力的联合概率密度Fig.4 Joint probability density of wind-PV power outputs

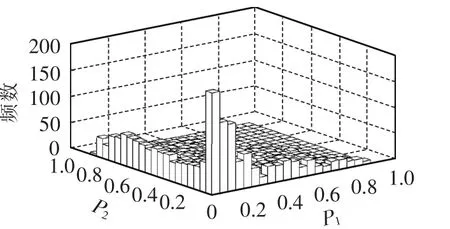
图5 风电场和光伏电站出力的统计直方图Fig.5 Statistic histogram of wind-PV power outputs

根据风电场、光伏电站出力的联合概率密度函数，通过积分运算得到风光互补电站的累积概率分布。设风电场装机容量为S1，光伏电站装机容量为S2，则风光互补发电系统总出力的累积概率分布可通过式（11）计算。

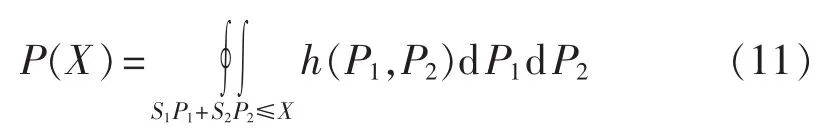
其中，X为风光互补电站出力，P（X）为风光互补电站出力的累积概率。

通过累积概率P（X）形成风光互补电站出力的停运表，由此建立风光互补电站的可靠性模型。该模型通过Frank Copula连接函数的相关参数θ，度量风电场和光伏电站出力之间的相关程度。因此，通过式（11）形成的风光互补发电系统的停运表，既包含了风电场、光伏电站出力的随机性，也包含了两者之间出力的相关性。

4 算例分析

4.1 可行性研究

以RBTS可靠性测试系统为研究对象，该系统装机容量为240 MW，其机组参数和小时负荷数据参见文献［15-16］。选取缺电小时期望值（HLOLE）和电量不足期望值（EENS）为可靠性指标，对算例系统进行可靠性评估。算例将测试系统中强迫停运率为0.02的40 MW机组替换为40 MW的风光互补电站，风电容量S1与光伏容量S2之比为10∶1。假定该互补电站的风速、光照特性与江苏沿海某风光互补示范工程相同。该工程共安装总装机容量200.25MW风电机组174台（1.5 MW双馈机组93台，0.75 MW的鼠笼式异步风电机组81台）；光伏电站总容量约20.004 MW。

实际示范工程中风电、光伏全年出力的Kendall秩相关系数τ=-0.161，算例中互补电站与其保持一致。同时计算了当替换容量分别为40 MW风电场和40 MW光伏电站时的系统的可靠性指标。结果见表2。

表2 可靠性指标比较（S1∶S2=10∶1）Tab.2 Comparison of reliability indices（S1∶S2=10∶1）

由表2可以看出，互补电站对算例系统的可靠性贡献接近于同容量的风电场，即风电在互补电站中起主导作用。光伏系统对算例系统可靠性的影响被较大的风光容量比（S1∶S2=10∶1）所掩盖。

为突出光伏系统的影响，以下研究中假定40MW互补电站中的风电光伏容量比为1∶1，其他计算条件保持不变。

将现场采集的200 MW风电场出力样本中每个元素缩小至原来的1/10，然后加上同一时刻20 MW光伏电站的出力，即形成风光容量比为1∶1的40 MW互补电站的出力数据，根据此数据计算的可靠性指标作为参考值。结果见表3。

表3 可靠性指标比较（S1∶S2=1∶1）Tab.3 Comparison of reliability indices（S1∶S2=1∶1）

通过比较，计算值与参考值相差很小，说明本文提出的方法是可行的。

4.2 不同季节的可靠性评估

根据互补电站的实际运行数据，以Kendall秩相关系数为相关性测度，计算一年四季风电、光伏出力的相关性，结果见表4。

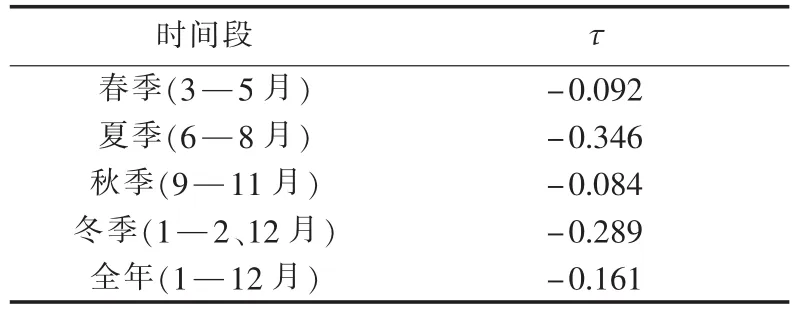
表4 不同季节风电光伏出力的相关性Tab.4 Correlation of power output between wind farm and PV station for different seasons

由表4可以看出，夏、冬两季风电、光伏出力存在一定的互补性；而春、秋两季风电、光伏出力仅存在微弱的互补性。

选取HLOLE为可靠性指标，对算例系统进行分季节可靠性评估。此时，互补电站出力由对应季节的实测数据折算而来。为了便于比较考虑相关性和不考虑相关性对可靠性指标的影响，引入相对误差：

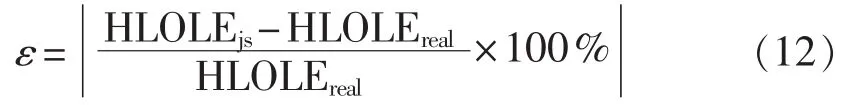
其中，HLOLEjs表示计算值，HLOLEreal表示按照由实测数据折算而来的出力数据计算所得的参考值。不同季节的可靠性指标见表5。

表5 不同季节的可靠性评估结果Tab.5 Results of reliability assessment for different seasons

由表5可知，在相关性较弱的春、秋两季，是否计及相关性对系统可靠性指标影响不大；但在相关性较强的夏、冬两季，考虑相关性的计算结果更接近实际情况。故在风电、光伏出力相关性较弱时，可以不考虑其相关性。但不排除某些地域的某些季节存在较强的相关性，采用本文提出的方法可以削弱相关性对可靠性计算带来的影响。

5 结论

本文基于江苏沿海某风光互补示范工程的实测数据，以RBTS标准测试系统作为算例，对风光互补发电系统进行可靠性评估，得出以下结论：

a.基于Copula理论，推导了风电场、光伏电站出力的联合概率分布模型，与实际统计值比较表明，该模型较好地刻画了同一地区风电场、光伏电站出力的联合概率分布特性；

b.建立了风光互补电站的可靠性模型，该模型不仅考虑了风电场、光伏电站出力的随机性，同时考虑了风电场、光伏电站出力的互补性；

c.采用本文建立的风光互补发电系统可靠性模型，对含风光互补发电系统的RBTS测试系统进行可靠性评估，计算结果表明本文方法可以较好地考虑出力相关性对可靠性的影响。