考虑多风电场出力相关性的电力系统随机优化调度

杨洪明 ，王 爽 ，2，易德鑫 ，易 俊 ，刘党峰

（1.长沙理工大学 电气与信息工程学院 智能电网运行与控制湖南省重点实验室电力与交通安全监控及节能技术教育部工程研究中心，湖南 长沙 410004；2.石狮市电力有限责任公司，福建 泉州 362700；3.中原油田供电管理处，河南 濮阳 457001）

0 引言

为了解决能源紧缺和环境污染问题，风力发电受到广泛的关注。但风速的间歇性和随机性使得风力发电具有不确定性的特征，这给大规模风力发电并网后电力系统的安全经济运行带来了巨大的挑战。为此，在含多风电场的电力系统优化调度中，需对风电场出力的不确定性进行概率分析，以实现风力发电机组的经济、安全调度。

目前，风电场出力的概率分析主要依据风速的Weibull、Rayleigh概率分布，利用风能转换系统的风速-出力函数关系推算得［1］。现有研究主要计算单个风电场出力的概率分布，忽略了多风电场出力之间的相互影响，从而降低了风电场出力概率分析的准确性［2］。在实际的电力系统运行中，往往存在多个风电场，特别是随着智能电网的建设，众多风电场接入系统。它们的风多来自同一风源，多风电场出力之间具有相关性。文献［3］考虑机组强迫停机率、尾流效应及气温等因素对风电场出力的影响，在假定各风电场出力相互独立的条件下，研究多风电场出力的联合概率分布。文献［4］基于Copula函数构建了电力系统不确定因素之间的联合概率计算方法，并采用Normal-Copula函数刻画出离岸风力发电和近岸风力发电之间的线性相关性。但风速的分布具有不对称的厚尾特性［5］，风电场出力的概率分布呈现出相应的不对称和厚尾特性（见第1、2节的分析），现有方法忽略了多风电场出力之间的这种尾部相关性。

随着风力发电的并网运行，在安排常规发电机组出力的同时，必须考虑风电场的发电能力。文献［6］在优化调度模型中，考虑了风力发电机组的出力约束和所需的旋转备用约束。但模型中风力发电作为确定性决策变量，忽略了风力发电的随机特性。风电场出力的不确定性会引起系统调度计划的调整，使得系统发电成本发生变化。为更好地实现系统调度的经济性和安全性，文献［7］考虑了风电场出力的随机特性，提出了基于最优潮流的随机优化调度模型，在目标函数中计及风力发电没有完全利用所带来的收益损失以及风力发电过分估计所造成的备用容量成本，并在约束中考虑了线路传输功率约束。文献［8］以概率的形式描述了风电场出力的随机性，并计及电动汽车及风电场出力的不确定性，构建了以系统发电成本期望为目标的优化调度模型。文献［9］以自回归滑动平均模型预测时变的风电出力，进而构建了含多风电场的电力系统经济调度模型。但上述优化调度模型均忽略了多风电场出力之间的相关性。为此，考虑多风电场出力的随机性和相关性，建立电力系统的随机优化调度模型有待进一步研究。

对随机优化调度模型的求解，文献［7-8］通过积分风电场出力概率密度函数来求取系统成本的数学期望，将随机优化调度模型转换成确定性优化问题。但随着随机变量数目的增多，多维积分的计算无法实现。通过蒙特卡罗抽样可以近似求取含多随机变量的系统成本期望，但未涉及机会约束的处理［9］。因此，有必要进一步研究随机优化调度模型的有效近似方法，将其转换为可计算的确定性优化问题进行求解。

针对现有研究的不足之处，本文利用Gumbel-Copula函数刻画多风电场出力的尾部相关性［10］，并构建其联合概率分布。在此基础上，提出了基于机会约束的电力系统优化调度模型，采用抽样平均近似SAA（Sample Average Approximation）法对机会约束进行处理［11］，将随机优化问题转换成可计算的确定性非线性规划问题，并通过粒子群优化PSO（Particle Swarm Optimization）算法进行求解［12］。

1 单风电场最大出力的概率分布

风速的不确定性一般通过 Weibull、Rayleigh、Lognormal等概率分布来描述。其中，两参数的Weibull分布被广泛使用，其概率密度函数为［13］：

其中，vws，m为风电场 m 的实际风速；kws，m和 cws，m分别为Weibull分布的形状参数和尺度参数，可由风速的样本数据通过最大似然法估计。

假设同一风电场内所有风力发电机组的风速和风向相同，用一台等效风力发电机组表示一个风电场。于是，单风电场的风速-出力函数关系可表示如下［14］：

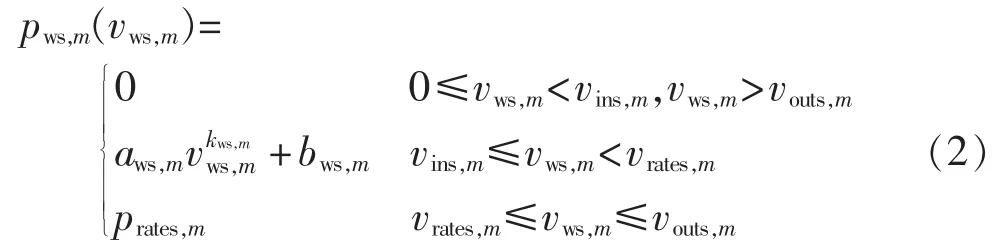
其中，pws，m（vws，m）为风电场 m 的最大出力函数；vins，m、vrates，m、vouts，m分别为风机的切入风速、额定风速及切出风速；prates，m为风机额定功率；aws，m、bws，m为功率特性曲线参数，且满足式（3）。

基于式（1）和（2），风电场 m 最大出力 pws，m的概率分布通过如下积分求得：

a.当 pws，m=0 时

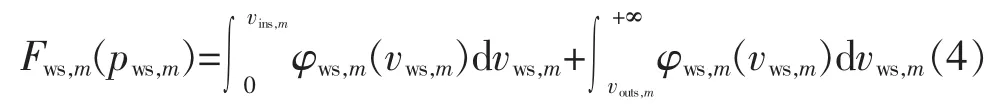
b.当 0＜pws，m＜prates，m时

c. 当 pws，m=prates，m时

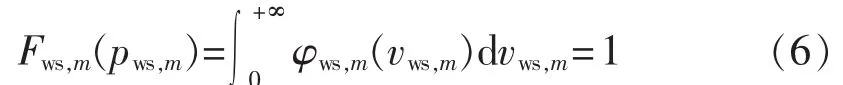
基于风电场出力概率分布式（4）—（6），图1显示出风电场最大出力（标幺值）的蒙特卡罗抽样数据和概率统计的直方图，其中风速数据来自荷兰De Bilt风电场的实时记录，详细情况见http：∥www.knmi.nl/samenw/hydra；设定风力发电机的切入风速、额定风速、切出风速分别为 3 m/s、13 m/s、25 m/s，标幺基准值为风电场出力的额定功率600 kW。由图1可以看出，风电场最大出力处于额定功率附近的概率最大，并且其概率值明显比风电场处于停机状态的概率大，风电场最大出力具有明显的上厚尾特性。

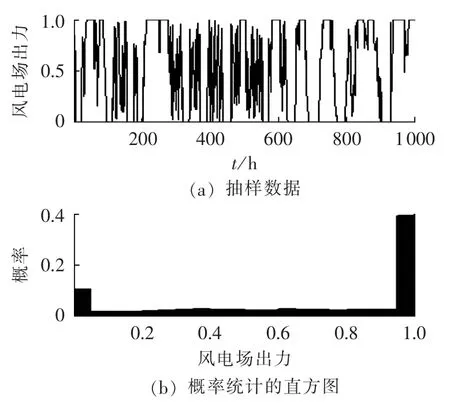
图1 风电场最大出力及其概率分布Fig.1 Maximum power output of wind farm and its probability distribution

2 多风电场最大出力的联合概率分布

同一风源下，受相同气象条件的作用，多个风电场的出力相互不独立。基于单风电场最大出力概率分布的厚尾特征，多风电场最大出力在额定功率附近同样具有较大的概率，即具有明显的非对称上厚尾特性。基于风电场出力概率分布式（4）—（6），图2进一步给出处于同一风源的荷兰De Bilt和Soesterberg两风电场最大出力概率分布的散点图，图中 Fws，Ⅰ、Fws，Ⅱ分别为风电场De Bilt、Soesterberg的最大出力概率分布。从图中可以看出，风电场最大出力的概率分布在额定功率附近的散点频数最大，上厚尾特征明显。表1进一步给出了同一风源下，多风电场最大出力的尾部相关系数。从表1可以看出，两风电场至六风电场的最大出力之间具有显著的上尾部相关性，而下尾部相关性不明显。其中ξU、ξL分别表示上尾部相关系数和下尾部相关系数，其数学定义为：

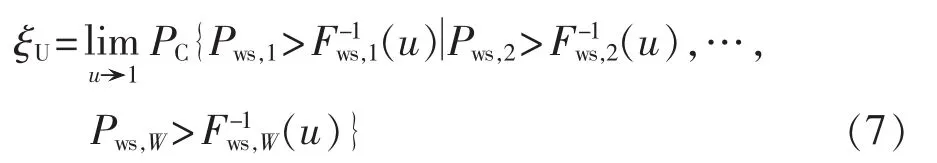
图2 两风电场最大出力的概率分布散点图Fig.2 Scatter plot of probability distribution for maximum power outputs of two wind farms

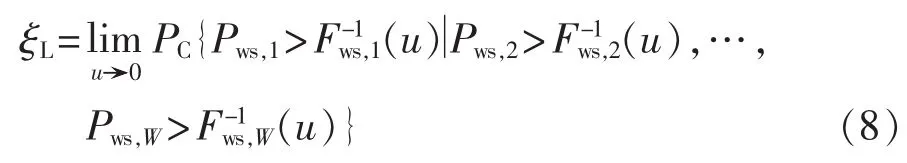
其中，PC｛·｝表示条件概率；W 为风电场数目；u∈［0，1］；表示 Fws，m（·）的逆函数。

表1 多风电场最大出力的尾部相关系数Tab.1 Tail-dependent correlation coefficients of maximum outputs of multiple wind farms

为准确估算多风电场出力的概率分布，下面借助Copula函数来实现多风电场出力的相关性建模。

Sklar定理：如果H（·）是边缘分布分别为 F1、F2、…、Fn的联合分布函数，则一定存在一个Copula函数 C（·）满足［10］：

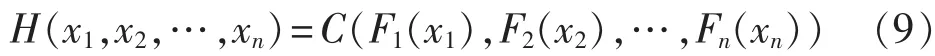
其中，H（·）为随机变量 x1、x2、…、xn的联合概率分布；F1、F2、…、Fn分别为单变量 x1、x2、…、xn的概率分布，且若 F1、F2、…、Fn连续，则 C（·）唯一确定。

由此可见，Copula函数本质为边缘分布到联合分布的映射，Sklar定理确立了Copula函数的一般性和唯一性。常用Copula函数有两大类：Ellipse-Copula族和Archimedean-Copula族。Ellipse-Copula族因密度等高线投影是椭圆而得名，主要包括Normal-Copula和 t-Copula；Gumbel-Copula、Clayton-Copula 和 Frank-Copula属于Archimedean-Copula族。

图3给出5种Copula函数的散点图。t-Copula、Frank-Copula和Normal-Copula属于对称分布，其中Normal-Copula不具有厚尾特性，t-Copula呈现出一定的厚尾特性；Frank-Copula不论在中心还是上下尾部，分布都比较均匀。Clayton-Copula、Gumbel-Copula属于非对称分布，其中Gumbel-Copula在上尾部比较集中，Clayton-Copula在下尾部比较集中。为此，Gumbel-Copula函数最适合构建具有非对称、上厚尾相关性的多风电场出力的联合概率分布，即：

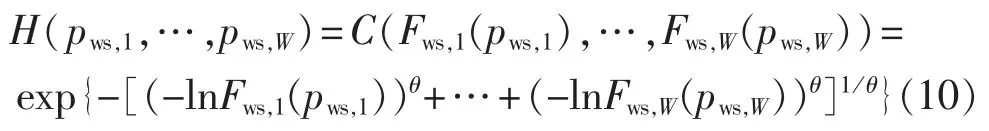
其中，C（·）为 Gumbel-Copula 函数；pws，1、pws，2、…、pws，W分别为风电场1、风电场2、…、风电场W的最大出力，对应的概率分布函数分别为 Fws，1（pws，1）、Fws，2（pws，2）、…、Fws，W（pws，W）；θ∈［1，+∞）为联合分布的联接参数，通过最大似然法估计。

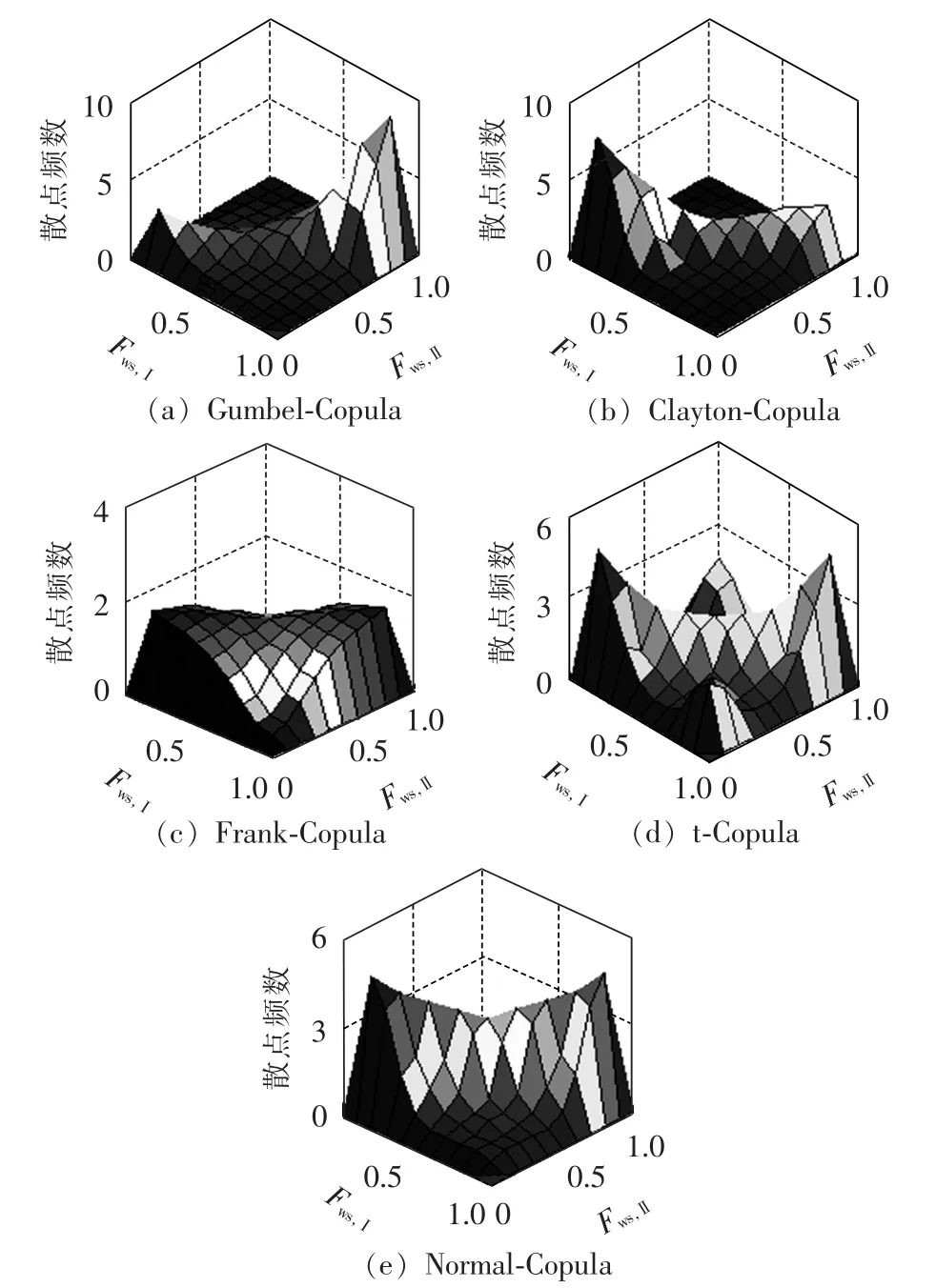
图3 5种Copula函数的三维散点图Fig.3 Three-dimensional scatter plots for five kinds of Copula functions

为验证Gumbel-Copula准确刻画多风电场出力联合概率分布的有效性，进一步开展柯尔莫格洛夫拟合优度 KS（Kolmogorov Smirnov）检验［15］。 多风电场出力实际样本数据的联合经验分布与Gumbel-Copula联合概率分布理论值的最大偏差为：

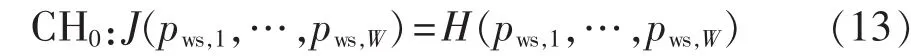
因此，1-R（λ）表示在临界点接受假设CH0的置信水平，通过1-R（λ）的大小可判断联合概率分布的拟合程度，1-R（λ）值越大说明拟合效果越好。

3 考虑机会约束的电力系统优化调度模型

由于风电场出力具有随机性和不确定性，在制定系统优化调度方案时，无法获得风电场出力的准确信息，从而使系统发电成本增加。为此，采用概率形式的机会约束反映风电场出力的不确定性，即在某一置信水平下满足风电场出力的相关约束［17］。基于此，含多风电场的电力系统随机优化调度模型为：

其中，Pgi为节点 i的常规发电机组发电功率，ai、bi、ci为发电成本系数，G为所有节点构成的集合。约束条件包括功率平衡约束、运行约束、线路传输约束，具体表示如下。

a.功率平衡约束：

其中，N为输电网的总节点数；Pwi为节点i的风电场输出功率；PLi为节点i的负荷功率。

b.运行约束：

c.线路传输约束：

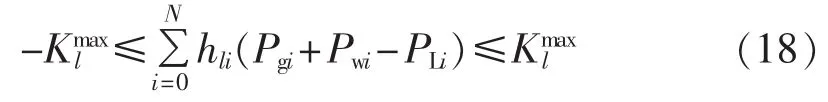
其中，hli为节点i的注入功率对线路l传输功率的灵敏度系数；为线路l的传输功率限值；线路l取1、2、…、L，L 为输电线路总数。

4 SAA法求解

机会约束的概率计算数学上需多维积分。随着风电场数目的增多，多维积分计算难以实现。为此，本文采用SAA法处理机会约束，将随机优化调度模型转化成可计算的确定性非线性规划问题［11］。该方法利用蒙特卡罗抽样抽取随机变量的样本数据，根据样本数据计算机会约束的概率，从而将机会约束转化成确定性约束条件。

采用最大函数，将一组约束等价成一个约束条件，即：

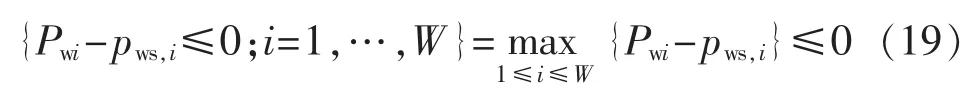
从Gumbel-Copula联合概率分布式（10）中，抽取 Q 组 W 个风电场出力的样本数据（j=1，…，Q），机会约束函数的概率期望值为：

利用（强）大数定律，Pagnoncelli等证明了当Q的取值足够大时，期望值式（20）以概率 w.p.（with probability）为 1 收敛于机会约束函数［11］，即：

在实际计算中，根据抽样次数与优化结果之间的关系、计算系统的性能和计算精度要求，确定合理的蒙特卡罗抽样次数。

于是，机会约束条件式（17）转化为确定性约束条件，即：

用式（22）代替式（17），电力系统随机优化调度模型式（14）—（18）转换成确定性优化问题，并采用PSO 算法进行求解［11］。

5 算例分析

5.1 多风电场最大出力的联合概率分布

根据荷兰De Bilt、Soesterberg、Leeuwarden 和Eelde风电场（分别设为风电场Ⅰ、风电场Ⅱ、风电场Ⅲ和风电场Ⅳ）的风速数据，利用最大似然法估计出各个风电场的Weibull分布参数，风速概率分布与实际样本的经验直方图比较，其拟合效果如图4所示。由图4可以看出，Weibull能较好地刻画风电场风速的概率特性。

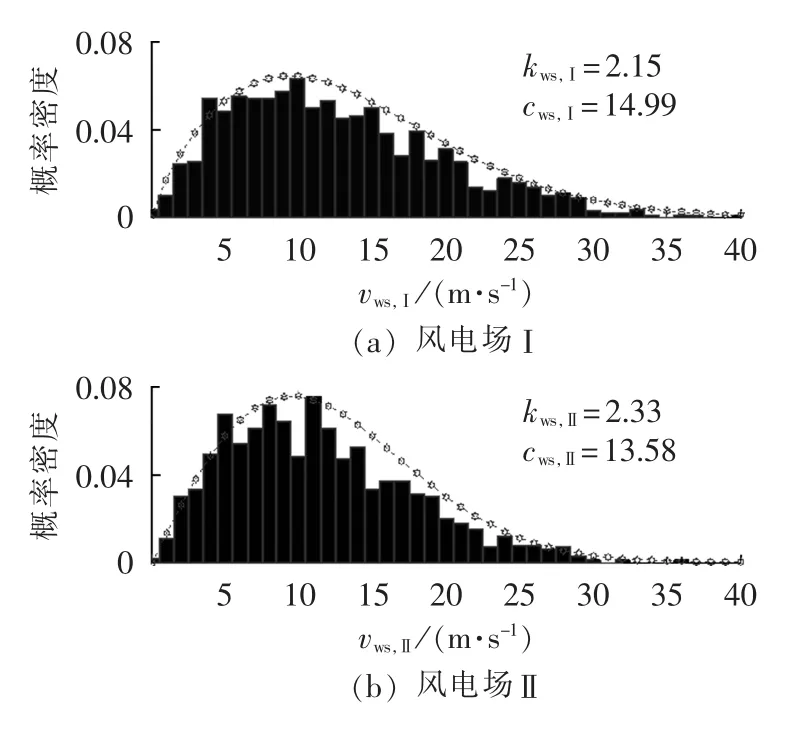
图4 风速概率密度拟合曲线Fig.4 Fitting curves of probability density for wind speed

基于风电场风速的Weibull分布，计算4座风电场最大出力及其概率分布，其中每个风电场均有40台相同的风电机组，每台风机的切入风速、额定风速、切出风速、额定功率均相同，分别为4 m/s、15 m/s、25 m/s、1.5 MW。利用5种Copula函数，构建两风电场（风电场Ⅰ和Ⅱ）、三风电场（风电场Ⅰ、Ⅱ和Ⅲ）、四风电场（风电场Ⅰ、Ⅱ、Ⅲ和Ⅳ）最大出力的联合概率分布，通过最大似然法估计联接参数。表2—4分别给出了联合概率分布的联接参数、尾部相关系数以及KS拟合优度。从中可以看出，与其他4种Copula函数相比，具有不对称上尾部相关特性的Gumbel-Copula能更好地构建多个风电场最大出力的联合概率分布，具有最小的拟合优度检验值。

表2 两风电场Copula函数参数估计及优度检验Tab.2 Parameter estimation of Copula function and goodness test for two wind farms

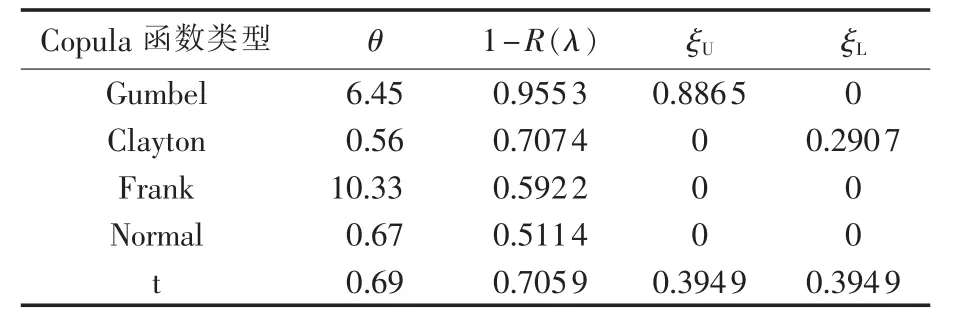
表3 三风电场Copula函数参数估计及优度检验Tab.3 Parameter estimation of Copula function and goodness test for three wind farms

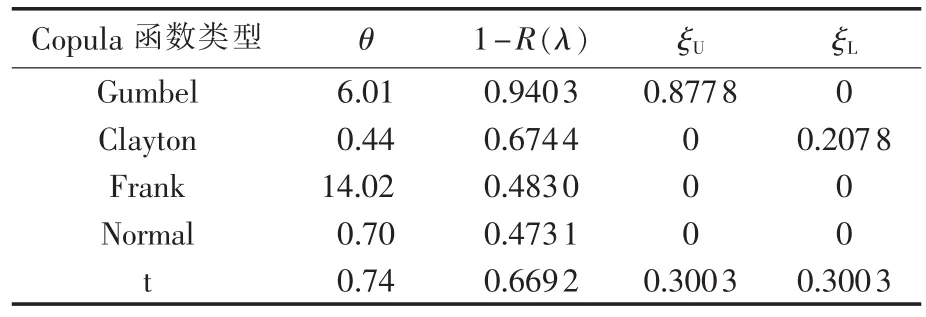
表4 四风电场Copula函数参数估计及优度检验Tab.4 Parameter estimation of Copula function and goodness test for four wind farms

利用Quantile-Quantile（QQ）图进行拟合检验，图5给出了两风电场最大出力的5种Copula函数的拟合效果（三风电场和四风电场最大出力的QQ图拟合具有相似的特点，限于篇幅，本文不再给出图形）。由图5可见，Gumbel-Copula较好地拟合了多风电场最大出力之间的尾部相关性（如表1和图2所示）。

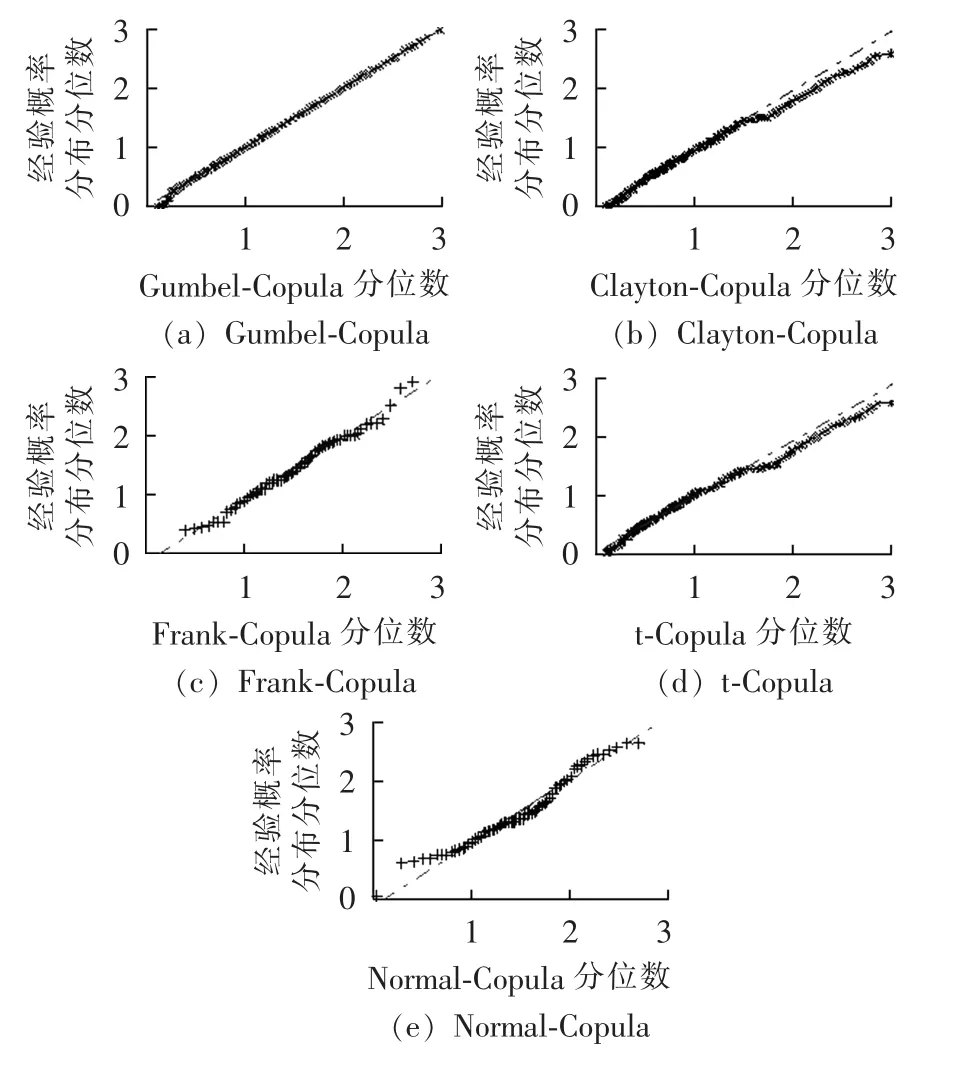
图5 5种Copula函数的QQ拟合图Fig.5 QQ fitting plots for five kinds of Copula functions

5.2 优化调度结果分析

本文采用IEEE 9节点系统验证所建优化调度模型及其算法的有效性。系统包括3个发电节点，其中节点2和3为风电场Ⅰ和Ⅱ的并网节点，系统基准容量为100 MV·A；节点1为常规发电机组的并网节点，其有功出力上、下限为 3 p.u.、0.1 p.u.；发电成本系数为 a1=0.085$/［（MW）2·h］，b1=1.2$/（MW·h），c1=600$/h。

PSO算法种群规模S=10，最大迭代次数dmax=100，学习因子设为2。当迭代次数为d时，惯性因子设为 ω=ωmax-（ωmax-ωmin）d/dmax，其中 ωmax=0.9，ωmin=0.4。

下面设计2种试验方案来验证本文所构建的随机优化调度模型的有效性。

a.情况1：联合概率分布对优化调度的影响。

根据风电场Ⅰ和Ⅱ最大出力的Gumbel-Copula联合概率分布求得2个风电场最大出力的期望值分别为0.246 p.u.、0.178 p.u.，并通过优化求解本文所构建的随机优化调度模型（机会约束的置信水平为0.98，在SAA法中蒙特卡罗抽样次数为1000），得到系统的最小发电成本为$7207.4。同时，若假设2个风电场最大出力的概率分布相互独立，即不考虑相关性时，2个风电场最大出力的期望值分别为0.237 p.u.、0.168 p.u.，得到系统的最小发电成本为$7398.6，如表5所示，表中出力均为标幺值。通过对比可以看出，根据Gumbel-Copula联合概率分布，考虑风电场最大出力的相关性，所得到的系统优化调度成本减少$191.2，即下降2.65%。

表5 不同联合概率分布下的优化调度结果Tab.5 Results of optimal dispatch for different joint probability distributions

b.情况2：置信水平和抽样次数对优化调度的影响。

针对本文所提出的随机优化调度模型，设置不同机会约束的置信水平，并在SAA法中采用不同的蒙特卡罗抽样次数，对应的优化调度方案及系统发电成本优化结果如表6所示。

表6 不同置信水平和抽样次数下的优化调度结果Tab.6 Results of optimal dispatch for different credit levels and sample times

从表6中可以看出，随着置信水平α的适当降低，节点2和节点3的风电机组出力增加，系统的发电成本降低，从而显示采用机会约束的合理性。同时，随着蒙特卡罗抽样次数Q的不断增多，SAA法近似误差减少，从而风电机组出力略有增加，系统发电成本降低。当抽样次数超过1000，优化计算出的发电成本值基本趋于稳定。因此，在计算中取Q=1000为合理的抽样次数。

6 结论

本文考虑多风电场出力的非对称、上厚尾相关性，采用Gumbel-Copula函数构建了多个风电场出力的联合概率分布，改进了多风电场出力的概率性分析；基于机会约束规划建立了含多风电场的电力系统优化调度模型，提高了优化调度的灵活性和鲁棒性；通过SAA法处理机会约束，将随机优化问题转化为确定性问题，从而简化模型的求解过程。最后，通过IEEE 9节点系统验证了所提出模型及其算法的合理性和有效性。