含直流电源与负荷的交直流系统潮流算法
傅 裕,杨建华,张 琪
(1.中国农业大学 信息与电气工程学院,北京 100083;2.北京电力公司密云供电公司,北京 101500)
0 引言
轻型高压直流输电技术以电压源换流器VSC(Voltage Source Converter)为基础,具有有功功率和无功功率独立控制、可向无源网络供电、换向可靠性高等优点,在高压直流输电和可再生能源发电系统中得到广泛应用[1-3]。
可再生能源发电单元一般包括直流网络[4],因此,含可再生能源电源的电力系统潮流分析应采用交直流潮流算法[5]。传统交直流潮流计算方法主要针对相控换流器[6-7],而VSC采用脉冲宽度调制PWM(Pulse Width Modulation)控制技术,其工作原理与基于相控换流器的交直流系统存在显著差异,因此,对于采用VSC技术的交直流电力系统,其潮流分析无法沿用传统的交直流潮流算法。文献[8-10]对轻型直流输电的交直流潮流计算方法进行了研究,给出了交替求解潮流算法;文献[11]最早提出了可嵌入牛顿法潮流计算的VSC数学模型,实现了对含VSC的交直流系统的潮流计算;文献[12]推导不同控制方式下交直流系统的潮流修正方程式,提出了VSC交直流系统潮流的统一迭代求解算法。这些算法中均没有直接处理可再生能源发电系统中的直流电源和直流负荷,收敛性也有待进一步改进。
本文在分析轻型直流输电技术特点的基础上,将VSC和直流网络嵌入牛顿-拉夫逊潮流迭代算法中,从交流网络、VSC和直流网络三部分推导了其相应的修正方程式,实现了包含直流电源和直流负荷的交直流电力系统潮流计算。
1 可再生能源发电与直流网络
近年来,太阳能和风力发电等可再生能源发电技术得到越来越广泛的应用。太阳能发电和蓄电池均为直流输出,在接入电网运行时需要通过逆变器转换成交流电。
风力发电机虽然为交流输出,但考虑到风速的随机性特点,目前,许多风电场使用VSC技术先将交流整流,再经逆变后接入大电网中[13-14]。
小型可再生能源发电系统,如农村户用风、水、光互补发电系统[15],需将各发电单元经过转换器和直流母线汇流,并接入统一的储能单元后再逆变成交流电,向用户供电或接入电网。此外,直流母线上有时还直接向直流负载供电。
2 基于VSC的交直流分界面模型
在基于VSC的交直流输电系统中,与VSC相连的交流母线称为交流特殊母线,采用变量i编号;其余交流母线称为交流普通母线,采用变量j编号。选取一个与母线i连接的VSC,编号为l,其稳态物理模型如图1所示,其中Psil、Qsil分别为从交流母线流向VSC的有功功率和无功功率;Rcil、Xcil分别为VSC等效电阻和换流电抗;Uti、Ucl分别为交流母线电压和VSC 输出基频电压;δti、δcl分别为 Uti和 Ucl的相位角;Pti、Qti分别为注入母线i的有功功率和无功功率;Pcl、Qcl分别为流入VSC的有功功率和无功功率;Udl、Idl分别为 VSC 的直流侧电压、电流;Ml、δl为 PWM控制系统的控制变量。
设 PWM 的直流电压利用率为 μl(0<μl≤1),调制度为 Ml(0<Ml≤1),则有:

图1 基于VSC的交直流输电模型Fig.1 Model of AC-DC transmission based on VSC

根据图1所示的电压关系,可以得到VSC从交流母线吸收的有功功率和无功功率:

3 含直流电源和直流负荷的交直流潮流计算方法
在研究交直流系统的潮流计算方法时,可以将该系统划分为交流网络、VSC和直流网络三部分,其中VSC作为交流网络和直流网络之间的中间联络环节,通过VSC的换流器方程形成交、直流网络的耦合关系。下面分别建立各部分的功率、电流不平衡方程,从而形成牛顿-拉夫逊法统一迭代的修正方程组。
a.交流网络方程。
对于交流普通母线,其功率不平衡方程可直接采用相应的牛顿-拉夫逊法潮流计算公式[6]。
对于图1中的交流特殊母线i,考虑到它与VSC存在功率交换关系,可以列出其功率不平衡方程:

其中,Ui和 Uj分别为交流母线 i、j的电压;Gij、Bij和θij分别为母线i与j之间的电导、电纳和电压相位差。
b.VSC方程。
由式(2)、(3)可得VSC的功率不平衡方程:
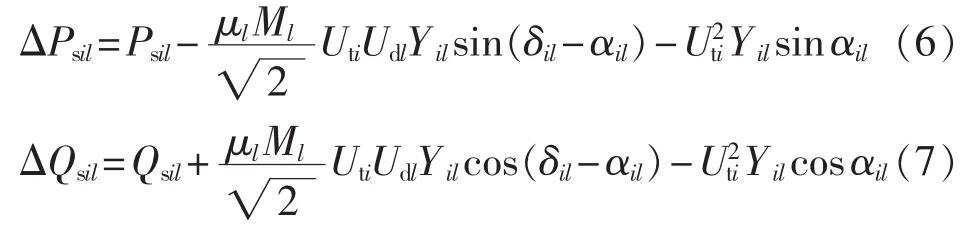
因换流桥的损耗已由电阻Rcil等效,故直流功率Pdl与注入换流桥的有功功率Pcl相等,有:

因此,换流桥的功率不平衡方程为:

VSC的直流侧与直流网络只有一对交互变量,即直流电压与直流电流,如图2所示。因此,VSC输出电流与直流网络有如下不平衡方程:

其中,Rdl为VSC连接直流支路的电阻;Udn为该支路连接的直流节点电压;n为直流母线编号。
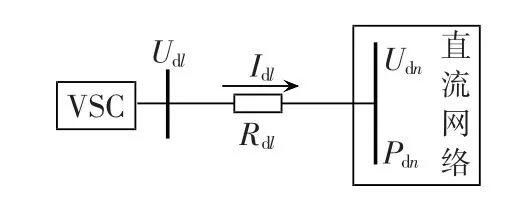
图2 直流网络与换流器的连接结构图Fig.2 Connection between DC grid and converter
c.直流网络方程。
对于直流网络中的直流节点,有:
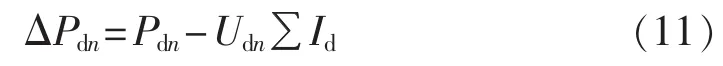
其中,Pdn为节点注入功率;为该节点所有支路及直流电源和直流负荷电流之和,流出方向为正;VSC输出端看成一条直流母线参与编号和计算。
对各支路有直流电流不平衡方程:

其中,Udn1、Udn2为该支路首、末端节点电压。
将各部分的功率及电流不平衡方程组合成基于VSC的交直流系统潮流计算修正方程式:
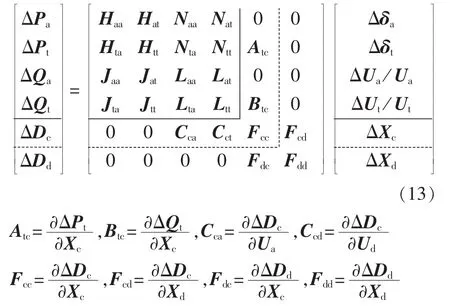
其中,ΔPa、ΔQa、ΔPt、ΔQt分别为交流系统普通母线和特殊母线的有功、无功不平衡量;Δδa、Δδt、ΔUa、ΔUt分别为交流电压相位角和幅值修正量;ΔDc=[ΔPsil,ΔQsil,ΔPcl,Δdl]T,ΔDd= [ΔPdn,Δdn]T,ΔXc= [ΔUdl,ΔIdl,Δδl,ΔMl]T,ΔXd= [ΔUdn,ΔIdn]T。 矩阵中以实线为界,左上角部分为交流网络的雅可比矩阵。
式(13)仅是含直流电源和直流负荷的交直流潮流计算时修正方程组的总体结构形式,而实际计算时需要根据VSC的不同控制方式[10,12]灵活地加以变化。基于VSC的交直流系统中VSC可以选择的控制方式有以下4种:定有功功率Pd及定无功功率Qd控制;定有功功率Pd及定交流母线电压Ut控制;定直流电压Ud及定无功功率Qd控制;定直流电压Ud及定交流母线电压Ut控制。例如,对应定直流电压控制的VSC,则修正方程组中不需包括ΔPsil和ΔUdl项;对应定交流母线电压控制时,则无ΔUt的修正方程。
另外还需注意,在 ΔDd、ΔXd中必须忽略与 ΔDc、ΔXc中重复的直流电流不平衡方程。
4 算例与分析
如图 3 所示,对 WSCC-9 节点系统[16]配以 VSC、直流电源和直流负荷,其中VSC1和VSC2分别连接于交流母线7和母线5上,VSC1采用定直流电压、定无功功率控制;VSC2采用定有功功率、定交流母线电压控制。VSC部分的主要电路参数为Rc71=Rc52=0.005 p.u.,Xc71=Xc52=0.12 p.u.;直流网络的电阻 RL1=RL3=0.02 p.u.,RL2=0.03 p.u.。 光伏电池按Ppv=0.4 p.u.定功率输出,直流负荷Pdc=0.2 p.u.。设直流电压利用率为1。

图3 修改的WSCC-9节点交直流系统Fig.3 Modified WSCC 9-bus AC/DC hybrid power system
潮流计算结果如表 1—5 所示,表中 Ud、Id、δ、M、Ps、Qs、Us分别为 VSC 直流侧电压、VSC 的直流侧电流、PWM调制波相角、PWM调制度、交流母线流向VSC的有功功率、交流母线流向VSC的无功功率、交流母线电压,所有电压、电流、功率均为标幺值。从表1中可见,该潮流算法可收敛于各VSC的控制目标。为验证计算结果的正确性,还使用了交替迭代法进行求解,得到了接近的计算结果。本实例中VSC1从交流电网吸收有功功率和无功功率;VSC2向交流电网注入有功功率,由于VSC2中输出电压高于相应的交流母线电压,使得VSC2能向交流电网提供无功功率。

表1 VSC部分交直流潮流计算结果Tab.1 Results of AC/DC power flow calculation for VSC

表2 直流网络计算结果Tab.2 Results of AC/DC power flow calculation for DC grid
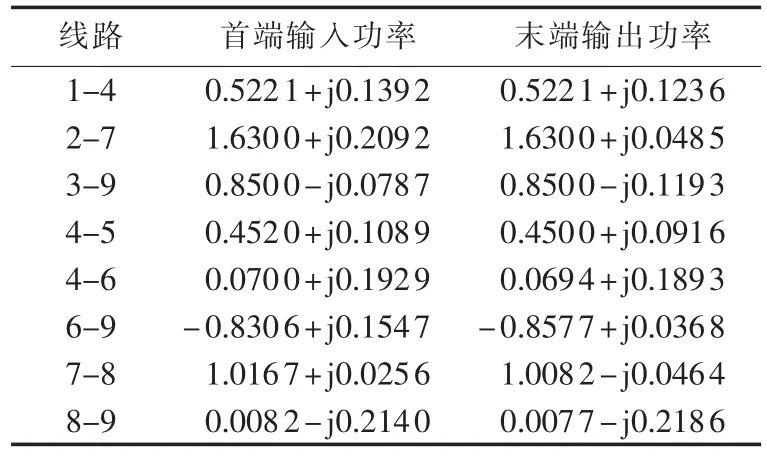
表3 交流支路计算结果Tab.3 Results of AC/DC power flow calculation for AC branch

表4 发电机出力Tab.4 Calculative results of generation output

表5 交流节点计算结果Tab.5 Calculative results of AC node voltage
5 结论
可再生能源发电单元的特殊性及轻型交直流输电的优越性,使得直流网络越来越多地融入现代电力系统,成为潮流计算中必须考虑的一部分。本文将VSC和直流网络的相关数学模型嵌入牛顿-拉夫逊潮流迭代算法中,提出了含直流电源和直流负荷的交直流系统潮流的统一迭代求解算法。潮流计算迭代收敛后,可求得交流母线的电压与相位、VSC的控制变量、直流节点电压和支路电流。以修改的WSCC-9节点交直流系统为例验证了本文潮流迭代算法的正确性和有效性。

