高频矩形波激励下磁芯损耗的研究

周 岩

（南京邮电大学 自动化学院，江苏 南京 210046）

0 引言

随着对开关变换器功率密度的要求不断提高，通常需要提升开关频率来降低开关变换器储能器件的体积［1-3］。铁氧体等磁性元件在开关变换器中起到储能、电能隔离等作用，工作频率的提高也就意味着磁性变压器损耗变得突出，磁性元件温升变高将显著影响开关变换器的性能与可靠性［1-4］。工作在不同的输入电压、输出电压和负载工作条件下，闭环开关变换器的工作占空比是不一样的，不同的拓扑结构也有自身的磁性变压器的激励特点。如何建立一个物理意义清晰的近似损耗模型，在工程中快速估算磁性变压器在不同激磁脉冲电压条件的损耗变化趋势，对于选择合适的变换器拓扑架构、优化磁性变压器的工作状态都具有重要意义。

1 铁氧体损耗模型

估算在高频条件、不同脉冲电压激磁条件下磁性元件损耗的研究历来得到学术界和工程界的重视，一直以来不断有大量的文献讨论，是理论界研究的热点问题之一。目前主要可分为三大类分析方法：数学统计类方法、傅里叶分解计算方法和磁性损耗分离法。

数学统计类方法最著名的经验公式是Steinmetz方程及其改进方法［5-7］，可表示为：

其中，Pcv是铁氧体磁芯损耗密度，C、α、β都是待定系数，根据磁芯的实际体积就可算出在一定频率和磁通密度变化量下的磁芯损耗。

Steinmetz方程忽略了磁芯形状以及尺寸的影响，认为磁损的功率密度仅取决于磁芯材料、激励信号频率以及磁感应强度。厂家通过大量的测试给出每种材料在一定工作区间条件下的系数。实验证明这是一个很好的近似，能极大地简化磁损的计算模型。通常磁芯供应商给出的都是磁损曲线对应于正弦波激励的情况下，但是由于开关变换器的工作特性，大多磁芯材料承受的激励波形是矩形波或接近于矩形波的谐振。因此有许多文献工作是采用在此方程基础上的改进方程，思路大多是通过引入各个变量在损耗分析中的权重，通过与实验结果对比用数学统计的方法给出近似的权重系数。

另外一种思路就是将任意的激励波形通过傅里叶级数分解为各谐波分量，分别计算各谐波分量下的磁芯损耗，然后求和得到磁芯总损耗［8］。由于磁芯材料与频率之间的关系并非理想线性关系，在高频率条件下磁芯材料早已失去磁性，显然这一方法存在较大误差。

磁芯损耗分离法通过分解磁芯总损耗中产生的不同机理，给出在不同条件下磁芯损耗的估算模型。磁芯损耗分离法的优势在于物理概念清晰，有利于工程师从本质上掌握磁损产生的机理，可合理设计磁芯的工作区间。文献［9-10］通过损耗分离的方法得出了方波激励条件下的损耗计算方法，但文中并未详细讨论脉冲的占空比改变时的磁芯损耗。

学术界已有很多的工作围绕着高频变换器不同占空比激励条件下的损耗展开研究，但是建立的模型普遍存在待定系数多、应用复杂、理解困难等问题，很难在工程设计中应用。本文首先对磁滞损耗和涡流损耗产生的不同物理机理进行详细分析，利用涡流损耗的大小与激励电压变化率的近似线性等效关系，提出了一种在不同占空比脉冲电压激励条件下磁芯涡流损耗变化趋势的计算方法。该方法可方便工程人员快速选择开关变换器拓扑，并为合理选择磁性变压器的设计提供指导思路。

2 双极性矩形波激励下的铁损模型

磁性变压器的磁损主要分为三部分：磁滞损耗、涡流损耗和残留损耗。在特别高频下表现显著的残留损耗是由磁化延迟及磁矩共振等造成的，因此在实际开关变换器磁芯元件设计中，主要考虑的是磁滞损耗与涡流损耗。

2.1 磁滞损耗模型

磁滞损耗是磁性元件磁化所消耗的能量，学术界对磁滞损耗建立了多种模型。建立在高频下的磁滞回线的数学表达式需要作许多近似和假设，而且要确定模型的参数要做大量的实验，计算过程复杂，需要确定的参数较多，一般很难用于工程计算。文献［9-11］认为激励频率、激励波形对磁滞曲线的影响可以忽略，只要磁通密度B的变化幅值相同，其磁滞损耗就相同，其大小为由激励波形形成的B-H曲线面积与频率的乘积。

在弱磁场激励下，图1（a）所示的抛物线磁滞损耗曲线与磁感应强度幅值的三次方、频率f成正比［9-10］，由此得到磁滞损耗密度的关系式为：

在较强磁场激励下，图1（b）所示的双线磁滞损耗曲线与磁感应强度幅值的二次方、频率成正比，由此得到磁滞损耗密度的关系式为：

因此，随着磁场激励的增强，磁滞损耗与磁通密度变化的指数关系从3变为2，与实际试验观测吻合。

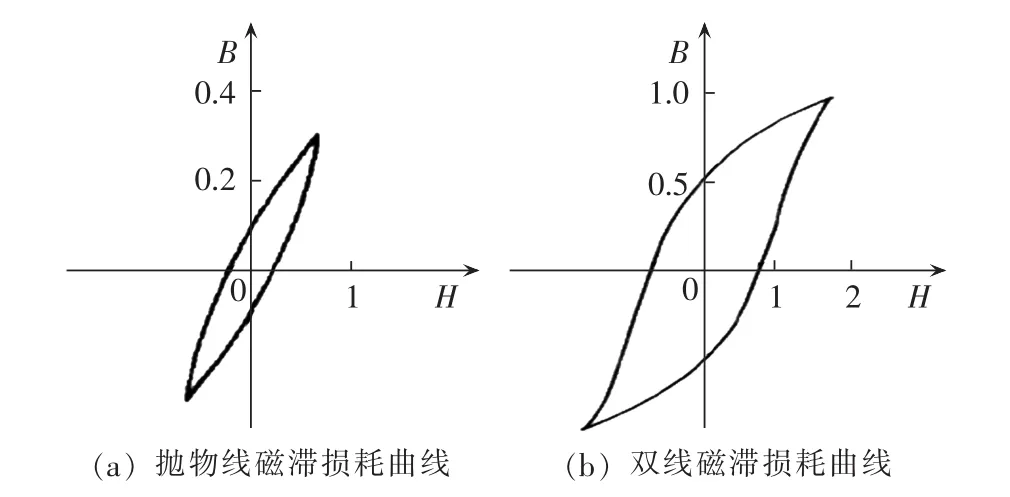
图1 简化的B-H曲线Fig.1 Simplified B-H curve

图2示出了开关变换器中磁性变压器两端承受的双极性激励电压波形，其关系为：

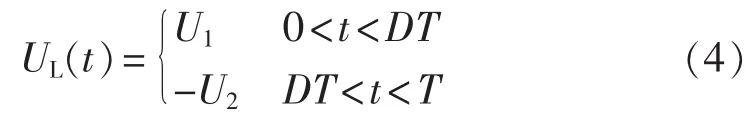
其中，D为占空比，T为开关周期。

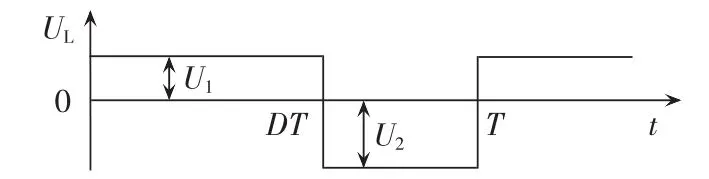
图2 高频变压器承受的激励电压Fig.2 Excitation voltage for high-frequency transformer

由法拉第定理易知：

其中，UL为加在磁性变压器上的激励电压，N为线圈圈数，Ae为磁性变压器的截面积。

为了防止磁芯饱和，在稳态工作时其承受的正负向伏秒面积应该相等。结合式（4）、（5）可知，对于选定的系统，在每个开关周期内磁性变压器磁通密度的变化幅值量为定值，即磁滞损耗的数值是一定的，不随着磁芯所承受的占空比激励电压的变化而变化，如图3所示。故可以近似认为磁芯材料厂家给出的正弦激励条件下的损耗曲线中就包含了相同磁通密度变化量时的磁滞损耗常量信息［9-11］。

图3 高频变压器的磁通密度变化曲线Fig.3 Flux density variation curve of high-frequency transformer

2.2 方波涡流损耗模型

涡流损耗主要是由交变磁场在磁芯中产生环流引起的欧姆损耗，与磁感应强度的变化率和磁芯材料的电阻率有关，不同波形激励下磁芯损耗的差异主要来自涡流损耗。

涡流损耗密度大小的一般表达式可表示为［9］：

式（6）说明涡流损耗大小与其承受的激励电压或磁通密度的变化率平方的平均值成正比。

磁芯厂家给出的损耗曲线一般都是基于正弦激励下，因此易知：

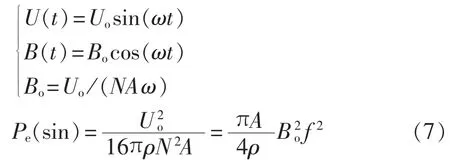
对于高频激励方波，其电压波形可用分段线性函数表示为：

结合式（7）和（8）得：

其中，Bo=UoT/（4NA）。

由涡流损耗的一般表达式（6）可知，在方波激励条件下其涡流损耗密度为：

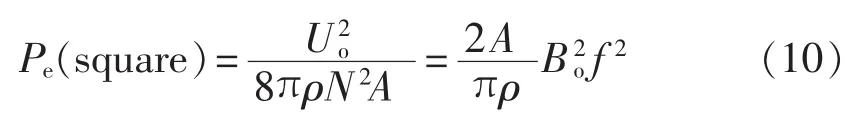
因此涡流损耗的模型可以用1个电感并联1个等效电阻表示，如图4所示。由式（10）得：

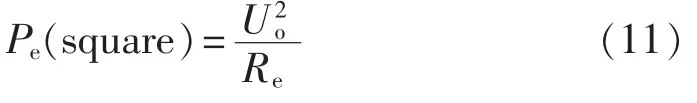
其中，Re=8π籽N2A为涡流损耗等效电阻，L为变压器激磁电感。通过合理的简化，使磁芯的等效阻抗Re在设计好的系统中转化为与频率、线圈匝数、磁芯截面积相关的常数，磁芯损耗成为与激励电压信号的幅值相关的函数。

图4 高频变压器涡流损耗等效模型Fig.4 Equivalent model of eddy current loss for high-frequency transformer

由式（7）和（10）可知，在相同频率和磁通密度变化量条件下，正弦波和方波激励涡流损耗密度的比值为［9，14］：

2.3 占空比矩形波激励涡流损耗模型

由于在不同工作条件下开关变换器的占空比是变化的，因此磁性变压器通常是承受伏秒平衡、磁通密度变化量相同的激磁电压［12-13］。因此，开关变换器中磁性变压器磁通密度变化量更一般的表达式为：

由式（13）可知，在每个开关周期内磁通密度的变化率大小与所承受的电压有关，其变化量相等且方向变化2次，如图2和图3所示。由于在不同占空比激励条件下磁芯磁通密度的变化量是相同的，由式（4）、（8）和（13）易得：

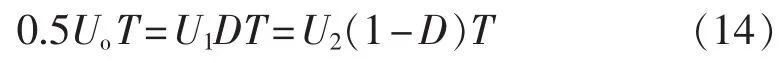
当占空比变化时，磁芯材料所承受的涡流损耗功率密度可表示为：

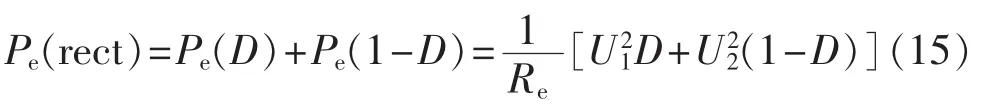
其中，Pe（D）为在占空比为D时激磁阶段涡流损耗功率密度，Pe（1-D）为在1-D去磁阶段涡流损耗功率密度。

式（15）具有重要的意义，将磁芯材料的涡流损耗特性与开关变换器实际工作状况联系起来，使磁性变压器在不同占空比激励下的涡流损耗转化为分段线性函数表达式之和。由于占空比的不同，在每个开关周期内激磁和去磁阶段的涡流损耗并不相同，如图5所示。由式（14）、（15）易得其关系式可表示为：

式（16）的结论与文献［13］采用的动态磁滞线模型并不矛盾，因为在本文中磁通密度变化率体现在激励电压和占空比的关系上，占空比越小，激励电压就越高，而涡流损耗与激励电压是二次方的关系，因此占空比越小时涡流损耗数值越大。

图5 激磁和去磁阶段涡流损耗比值曲线Fig.5 Curve of eddy current loss ratio of magnetizing period to demagnetizing period

由式（12）和（15）可知，任意占空比的矩形波与方波激励条件下产生的涡流功耗密度的比值可表示为：

结合式（12）、（17）、（18），就可以求出在不同占空比条件下矩形波激励涡流损耗与方波激励和正弦波激励的关系式：

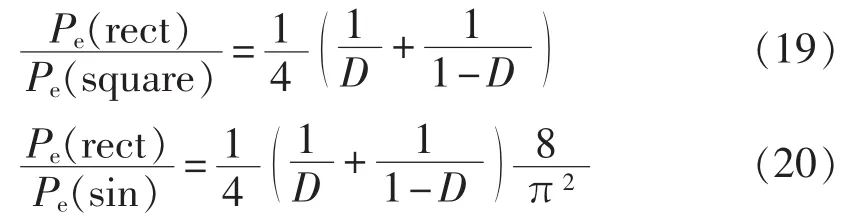
将不同的占空比代入式（19）、（20），就能得到在不同占空比激励下涡流损耗与方波和正弦波激励下的对比关系，如表1所示。

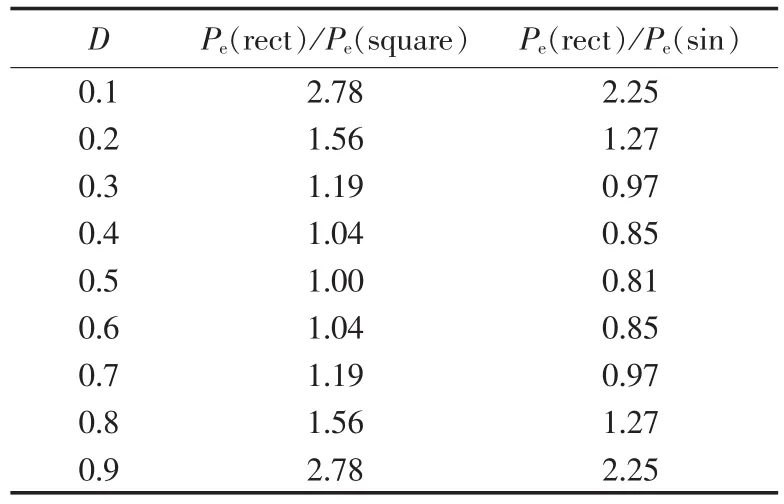
表1 不同激励下的涡流损耗比值Tab.1 Eddy current loss ratio for different excitations

从表1可以得出以下结论：

a.当占空比为0.5时，涡流损耗最小；

b.随着占空比的上升或下降，涡流损耗值都会增大；

c.涡流损耗的比值关于占空比D=0.5轴对称，如图6所示。

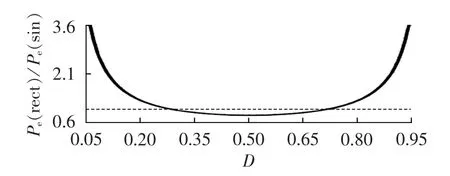
图6 矩形波与正弦波激励的涡流损耗比值曲线Fig.6 Curve of eddy current loss ratio of Pe（rect） to Pe（sin）

图6给出了其变化趋势图，可以发现占空比D=0.283和D=0.717是与正弦激励损耗的分界点，它们之间的磁芯损耗关系可表示为：

式（21）所得结论与文献［12］用测量统计方法得出的结论一致，同时也与文献［13］采用等效磁损模型得出的磁损变化趋势吻合，验证了所提理论正确性。

3 实验验证

图7为3F3铁氧体材料在D=0.75、ΔB=0.336、fs=200 kHz时测试的动态磁损回环曲线［13］。从图7可以看出在每个磁化周期，S1对应的D=0.75损耗面积明显小于S2对应的D=0.25损耗面积。S2对应的去磁阶段涡流损耗是S1对应的激磁阶段涡流损耗的3倍，本文提出的式（16）很好地解释了此现象。

图7 矩形波D=0.75的磁芯损耗回线Fig.7 B-H waveform excited by rectangle waveform with D=0.75

为了测量不同占空比对磁损的影响，可采用图8所示的不对称半桥实验电路验证。将示波器测得的电压、电流信号相乘并累加后求平均值，所得的结果就是磁芯损耗。由于测量变压器的是一次侧电流以及二次侧感应电压，线路上的其他损耗以及变压器铜损并没有包含进来［12］。

图8 测试电路Fig.8 Measurement circuit

本文采用Magnetics 0F-44925-TC磁芯在不同占空比条件下获得的磁芯损耗实验数据验证所提出的损耗模型的正确性［12］。图9示出了fs=50 kHz激励条件下磁通变化量分别为100mT、150mT、200mT、250 mT时磁芯在不同占空比矩形波激励条件下的功耗曲线，从图中可以看出在占空比D=0.5时磁芯损耗最低，此后不管占空比增大或降低，磁芯损耗近似对称增加。

图9 50 kHz矩形激励下磁芯损耗实验数据Fig.9 Experimental data of core loss excited by 50 kHz rectangle waveform

图10示出了fs=75 kHz激励条件下磁通变化量分别为100 mT、150 mT、200 mT时磁芯在不同占空比矩形波激励条件下的功耗曲线。同样从图中可以看出在占空比D=0.5时磁芯损耗最低，此后不管占空比增大或降低，磁芯损耗近似对称增加。

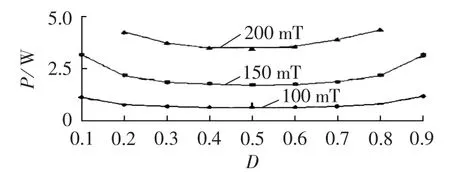
图10 75 kHz矩形激励下磁芯损耗实验数据Fig.10 Experimental data of core loss excited by 75 kHz rectangle waveform

磁滞损耗的大小为基本磁滞回线包围的面积与频率的乘积，在相同频率和磁通密度变化量下磁滞损耗可近似认为是常量，而占空比引起的激励波形变化对磁滞回线包围面积的影响很小［9-11］。因此磁芯整体损耗实验数据的变化趋势主要反映了占空比对涡流损耗的影响。在整体损耗测试数据中分离出磁滞损耗是下一步工作的重点。图9和图10实验结果验证了本文所提出理论的正确性，在同样频率和磁通密度变化量作用下，涡流损耗的大小在不同占空比作用下增加或降低，整体磁芯损耗以D=0.5为轴心对称增加，和理论分析的变化趋势是吻合的。

4 结论

磁性材料规格书中一般只提供正弦激励下的磁芯损耗参数，如何建立合理的损耗模型，分析在不同占空比脉冲电压激励下磁性变压器的损耗变化一直是学术界研究的热点之一。

本文根据损耗分离的思想，结合开关变换器磁性变压器实际的工作状态，提出了在不同占空比条件下磁损的分析方法。由于占空比的不同，在每个开关周期内激磁和去磁阶段的涡流损耗并不相同。本文指出当占空比D=0.5时，磁芯损耗最小；当占空比D＞0.5或D＜0.5时，磁芯损耗都将增加；当占空比D=0.283或D=0.717时，占空比激励下的磁芯损耗与正弦波激励下的损耗相等。

本文所提出的损耗分析方法物理概念清晰，易于理解，理清了不同损耗之间的关系，对于优化磁性变压器的效率、合理确定开关变换器的工作区间具有重要意义。最终结论没有复杂的计算公式和大量的待定系数，实验结果验证了本文提出理论方法的准确性。需要指出的是，本文结论并未涵盖存在较大直流偏置时磁损的计算（PWM功率变换器中的变压器中一般无直流偏置），针对这类场合的研究将会在后续论文中加以讨论［15-16］。