规划配电网简化方法及其可靠性评估算法

邱生敏，管 霖

（华南理工大学 电力学院，广东 广州 510640）

0 引言

电网停电事故绝大部分是由配电网引起的，配电网的可靠性是供电企业考核的重要指标之一。因此，提出一套适用于实际配电网的可靠性评估算法是非常必要的。

配电网的可靠性理论计算和评估主要有蒙特卡洛（Monte Carlo）模拟法和解析法两大类方法。目前解析法主要有基于故障后果分析法的改进算法：最小路法［1］和改进的故障后果分析法［2-3］；此外，文献［4-5］提出了可靠性指标递归方法；文献［6］提出了容量约束在可靠性评估中的应用；文献［7-9］考虑了开关故障对可靠性的影响；随着智能电网的发展，考虑分布式电源的可靠性评估［9-11］也随之出现。

然而，上述算法均是对运行中的配电网进行可靠性评估，并不适用于规划配电网的可靠性评估。对规划网架的可靠性评估有利于指导供电企业的配电网建设以及改善网架结构。

考虑到规划配电网存在用户信息不全、配电网具体结构不清晰等特点，本文首先对规划网架进行简化假设，在此基础上提出了一种适用于规划配电网的可靠性评估算法。

1 可靠性算法原理分析

1.1 配电网网络简化和假设条件

传统的配电网可靠性评估需要对各种元件进行故障枚举，包括开关、配变、线路等。本文对配电网网络元件进行组合，以减少枚举元件数量。如图1所示，F1和F2表示馈线编号，T表示变压器，S表示负荷开关，N/O表示常开负荷开关，L表示电缆线路。图1的方框组合了一个电房的负荷开关及熔断器，大幅减少了元件数量。

图1 配电网馈线结构Fig.1 Structure of distribution feeder

本文规定：馈线断路器QF1到联络线之间的任何一个电房组合称为一个主干段，如图1的电房1、电房2和电房3；主干电房与电房之间连接线路也称为一个主干段，如线路L1、L2和L3。所有主干段串联构成了主干线。主干段引出的电缆线路和电房称为分支线，如线路L4和电房4称为一个分支线。

对其中一个电房进行分析，如电房1组合了负荷开关S1、S2和3个熔断器，则电房1的故障率λi（单位：次 /a）和故障修复时间 ti（单位：h/次）为：

其中，λk、λr和 λb分别为开关、熔断器和配变的故障率；tk、tr和tb分别为开关、熔断器和配变的故障修复时间；p为配变熔断器的正确动作率。

经上述处理，可靠性计算中无需对每个负荷开关进行故障枚举，而只需枚举组合电房及电缆线路。

一回馈线中，假设主干线的电缆段数（k）和主干线的电房数之和为m。对于开关组合的电房，故障率λi和故障修复时间ti根据组合电房开关数通过式（1）计算，对于电缆线路，λi和 ti计算如下：

其中，λL、tL、Lg分别表示电缆线路故障率、修复时间和主干线的长度。

尽管作了上述简化，在规划配电网中，仍然不能获得每个负荷点具体配变台数和用户数，也不能获得每段主干线的具体长度，而只能大概估计馈线总的配变用户情况和主干线总长度。

因此，本文在可靠性评估中假设规划配电网有以下特点：

a.馈线各主干段的配变台数和容量相同，用户数也相同；

b.馈线各主干段的电缆长度相同；

c.多级分支简化为一级分支，分支线和主干段的用户分布平均。

上述假设的合理性和正确性将在后文的误差分析中进行验证。

1.2 转供率计算方法

严格意义上，一回馈线可以供电的负荷需要经过潮流计算确定。但是，一方面，即使在运行的配电网目前也难以掌握每台配变的负荷曲线，也就难以获得配网潮流计算需要的基础负荷分布，因此只能按配变平均功率因数和平均负载率来粗略估算每个配电点的负荷；另一方面，开环运行的配电网源流关系清晰，潮流计算只不过补充了因网损带来的附加电流信息。考虑到配电网馈线的最大允许电流设定值本身留有一定的裕度，因此忽略网损对评估馈线的可供电负荷影响。

为此，本文采用以下方法直接估计每回馈线允许的挂接配变容量，并以此表示馈线可供电负荷：

a.根据馈线截面和型号确定允许最大电流Imax；

b.根据统计值确定配变平均负载率，记为γ，一般取值为 0.85～0.95；

c.根据统计值确定馈线上用电负荷的同时率，记为α，一般取值为0.7～0.9。

则馈线挂接的配变容量之和S必须满足：

可靠性算法采用故障枚举的思路，逐段评估每个馈线段故障造成的用户停电范围和停电时间。对于一个制定的故障段，显然其上游区段的全部用户均可在故障段隔离之后，通过馈线首端重合闸来恢复供电，不需要经联络馈线转供。令其下游区段的配变容量为Sx，则馈线联络线可转供负荷需要通过比较Szg与Sx来确定。本文定义转供率ρi为：

ρi取值范围为［0，1］。 如果 ρi＞1，则取值为 1。

1.3 基于故障枚举的可靠性指标形成

由于10 kV配电网采用环网接线、开环运行方式，运行时每回10 kV馈线的有功功率流向均为从电源点到末端的树状放射式结构。当不计出线断路器不正常故障在变电站10 kV母线引起的事故放大时，各回10 kV馈线的运行是彼此独立的，其停电时户数和停运容量等指标都可以直接叠加形成整个系统的可靠性指标。

基于前文配电网网络化简和假设，得出每个主干段i的故障率λi和修复时间ti后，还需给定电网的评估转供电操作时间tz和平均故障隔离时间tG。

则对任一回馈线，故障引起的用户停电时户数nSH和停电损失电量Q可按主干线故障、分支线故障、配变故障分别计算如下。

a.主干线故障：

b.分支线故障：

其中，N为馈线上的总用户数；Ni和Si分别为第i段分支线上的用户数和配变容量；f为馈线分支线数目；S 为馈线挂接配变容量之和；λL、tL、Lf分别为电缆线路故障率、修复时间和一个分支线长度。

c.配变故障：

其中，SN为单台配变的容量；p为配变熔断器正确动作率；k为馈线配变台数。

上述三部分之和即为一回馈线的停电总时户数和总电量。

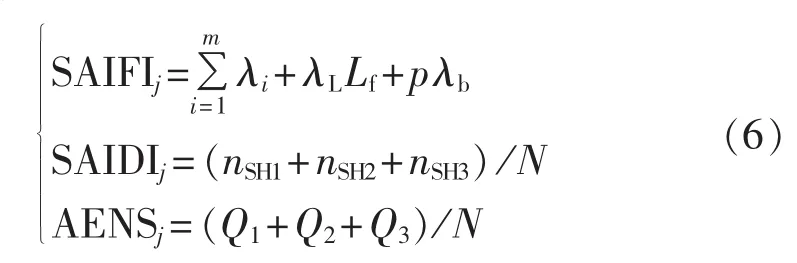
系统所有馈线之和为全系统的停电时户数和损失电量。则系统可靠性指标如下。

系统平均停电次数指标：

系统平均停电持续时间指标：

系统供电可靠率指标：

用户平均停电缺供电量：

其中，j为馈线序号；Nj为馈线j的用户数。

1.4 假设条件误差分析

第1.1节提出了规划配电网的假设条件，对负荷和线路段作了均匀化假设，实际配电网馈线并不服从均匀分布，因此有必要对相关假设进行验证。

假设1：馈线各主干段的配变台数和容量相同，用户数也相同。

图2（a）、（b）、（c）分别给出了主干段负荷均匀分布、集中在首端、集中在末端3种情况，其中（a）是规划网架的假设条件的要求。计算3种情况的馈线的平均停电时间次数指标SAIDI结果分别为0.412、0.408 和 0.416，（b）、（c）与（a）的相对误差仅 1.06%，证明此假设可以适应可靠性指标评估。

图2 主干段负荷分布Fig.2 Load distribution on main trunk

假设2：馈线各主干段的电缆长度相同。

如图3所示，（a）给出了各主干段电缆长度相同情况，而（b）和（c）分别给出了主干线电缆长度首段较长以及末段较长的2种情况。计算3种情况的馈线的平均停电时间次数指标SAIDI结果分别为0.412、0.415 和 0.410，（a）与（b）相对误差仅 0.61%，与（c）相对误差也是0.61%，证明该假设是合理的。

图3 主干段之间电缆分布Fig.3 Cable distribution between main trunks

假设3：多级分支简化为一级分支，分支线和主干段的用户分布均匀。

在规划配电网中，并不能清晰获得馈线多级分支的级数和具体负荷情况，因此本文算法只考虑一级分支的情况，并对多级分支简化到一级分支进行误差分析。

图4中（a）是规划网架假设条件的要求，（b）包含多级分支，简化之后如（a）所示，即多级分支简化为一级分支，具体的误差将在算例中验证。

2 可靠性计算数据结构介绍

根据可靠性计算要求，本文数据结构的基本的数据表包括4个部分。

a.根据大量历史数据统计以及广东某市区实际配电网运行情况，分析得出配电网基本元件的故障率和故障修复时间如表1所示。该配电网故障参数表用于存储电缆、架空线路、配变、断路器、负荷开关、熔断器等元件的故障率λ和故障修复时间t。

b.配电网管理参数与供电局管理水平以及配电网自动化实施情况有关，表2是在参考广东某地区供电局实际情况基础上给出的推荐值。该配电网管理参数表用于存储转供电操作时间tZ、故障隔离时间tG以及熔断器正确动作率p。

图4 分支线简化Fig.4 Simplification of branches

表1 配电网元件故障率和故障修复时间Tab.1 Failure rate and repair time of distribution components

表2 配电网管理参数Tab.2 Management parameters of distribution network

c.公用馈线信息表用于存储规划配电网架的基本馈线信息。根据上述可靠性算法基本原理，公用馈线信息表包括：馈线基本信息，含馈线的编号、馈线所属变电站、馈线所属的分区名称；馈线用户信息，含馈线配变台数、馈线的配变容量、馈线用户数；馈线10 kV设备信息，含馈线主干线长度Lg、馈线总长度Lz、主干线的线路型号、馈线主干线电房数；馈线网架结构信息，含主联络线编号、主联络线编号接入馈线的位置、分支线数目、分支线分布在主干段的位置。

d.可靠性评估结果表用于存储各回馈线可靠性计算结果以及系统可靠性计算结果，存储的指标包括：馈线/系统的用户数、馈线/系统的平均停电次数SAIFI（单位：次/（户·a））、馈线/系统的平均停电时间 SAIDI（单位：h/（户·a））、馈线/系统的平均缺供电量 AENS（单位：kW·h/（户·a））、馈线/系统的供电可靠性 RS（单位：%）。

3 算例系统分析

为了验证本文对规划配电网的简化假设的合理性以及算法的正确性，选取广东某市区的3回馈线结构进行计算，如图5所示。

3回馈线的基本信息如表3和表4所示。

表3 公用馈线用户信息Tab.3 User information of public feeder

表4 公用馈线线路设备信息Tab.4 Equipment information of public feeder

各回馈线的联络信息和分支线信息可以从图5中看出。

运用本文对算例的网架进行简化假设，利用本文算法得出系统的平均停电次数SAIFI、系统的平均停电时间SAIDI、系统的平均缺供电量AENS、系统的供电可靠性RS，并与不作简化假设的精确网架计算结果进行对比，结果如表5所示。

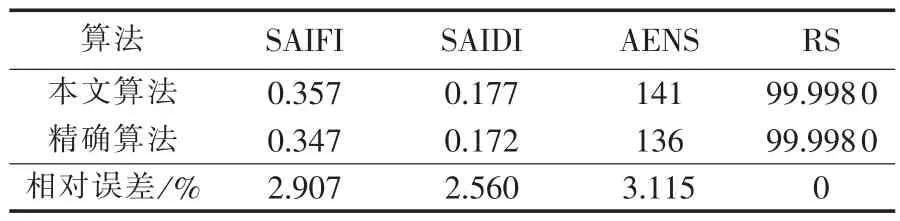
表5 系统可靠性计算结果分析Tab.5 Results of system reliability calculation

其中精确网架是指不对配电网结构进行简化，采用故障后果分析法对配电网进行可靠性评估，具体方法参见文献［3］。

由表5看出，虽然本文对规划配电网结构作了3种假设，简化了可靠性计算需要的基础数据，但是计算结果与精确算法的计算结果相近。系统的平均停电次数SAIFI和系统的平均停电时间SAIDI误差在3%之内，系统的平均缺供电量AENS误差在4%之内，并且供电可靠性RS误差在小数点4位之后，几乎没有误差。所有误差均在5%之内，对于规划配电网，这个误差在允许范围内。

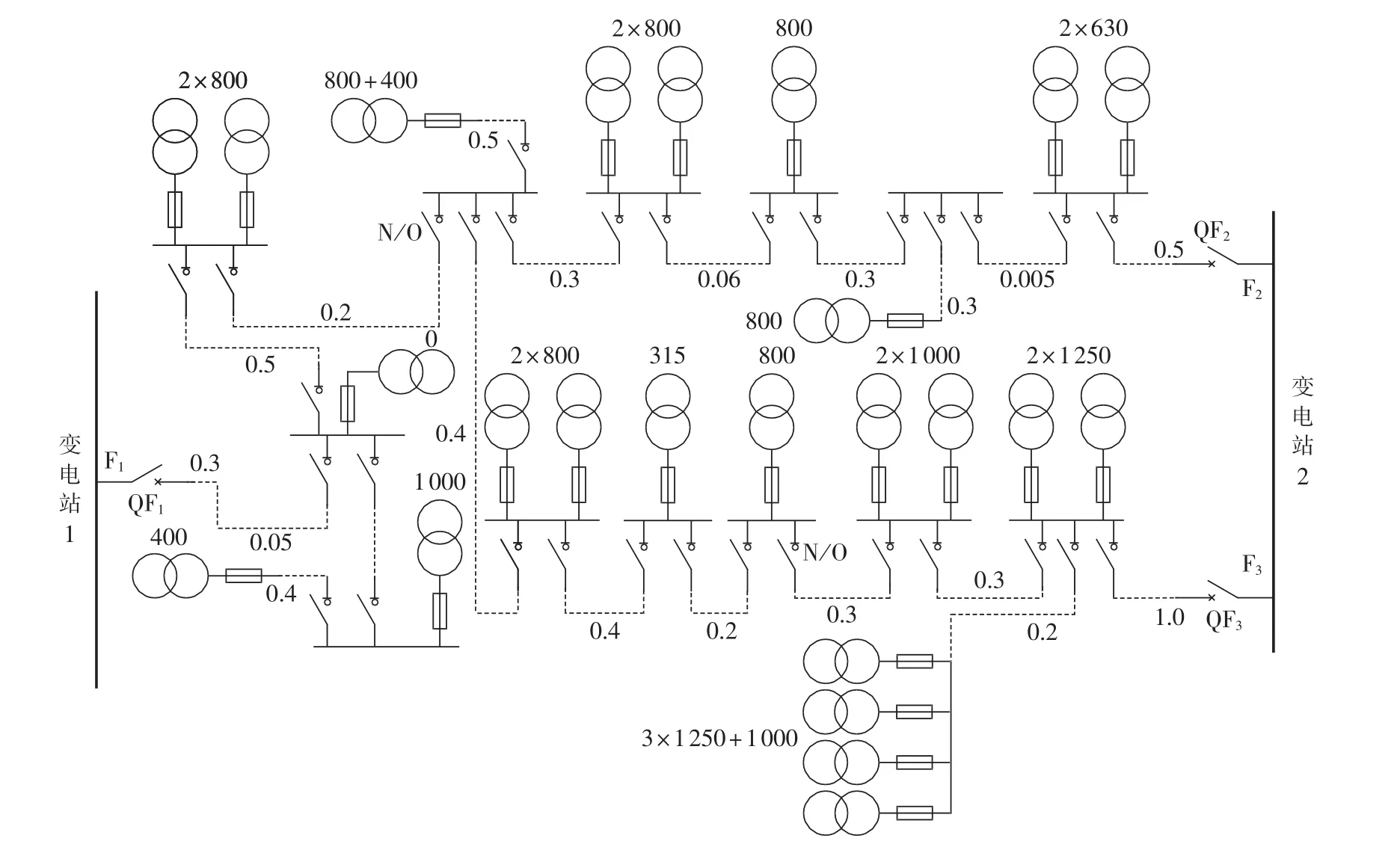
图5 广东某地区馈线结构Fig.5 Feeder structure of an area in Guangdong

4 结论

目前配电网可靠性评估主要是针对运行中的电网，对于规划配电网，并没有有效的评估方法。本文提出了一种规划配电网可靠性评估算法。

a.针对规划配电网数据不完善特点，对规划配电网进行简化假设，假设馈线的负荷均匀分布并且各个主干长度相同，并对简化网架进行误差分析。考虑到故障后负荷转供问题，提出了转供率计算方法。最后把配电网馈线分为主干线、分支线和配变三部分，分析各个部分对可靠性指标贡献，由此推导出馈线可靠性指标，再由馈线可靠性指标计算系统可靠性。

b.分析了规划配电网可靠性计算需要的数据结构，包括可靠性计算基础参数、配电网公用馈线信息表和可靠性计算结果表。

算例表明本文对规划配电假设的合理性和算法的可行性，该算法可以运用于实际大规模规划配电网的可靠性评估。