基于改进变尺度混沌优化算法的微网优化运行

张双乐 ，李 鹏 ，陈 超 ，施儒昱

（1.华北电力大学 新能源电力系统国家重点实验室，河北 保定 071003；2.江苏省电力公司苏州供电公司，江苏 苏州 215004）

0 引言

微网是一种由负荷、微电源（分布式电源）和储能装置共同组成的有机系统。微网可以有效地整合各种新能源发电技术，充分发挥新能源发电所带来的经济效益和环境效益；可以更好地满足用户对电能质量和供电可靠性更高的要求；可以实现电网的削峰填谷，提高能源的利用率［1-3］。

微网的优化运行是微网研究的重点和难点问题，已经引起了人们的广泛关注。微网的优化运行主要有如下几个特点：由于微网主要接入配电网中，电压等级低，系统中输电线路的电阻起主导作用，线路损耗较大，不能忽略［4］；由于风力发电、光伏发电等新能源发电技术受自然环境的影响较大，输出功率具有随机性、波动性、间歇性，微网的优化运行要求实时性比较强，一般在秒级；由于微网内的微电源与传统的火电机组有很大的区别，不能简单应用等耗量微增率准则，一般采用智能优化算法来进行优化。

混沌优化算法具有遍历性、随机性、规律性的特点，能在一定的范围内按照自身的规律不重复地遍历所有的状态［5］。混沌优化算法能避免陷入局部极小，比随机搜索更具有优越性，易于跳出局部最优解［6］。文献［7］将混沌优化算法用于电力系统经济负荷分配，并与遗传算法相比较，证明了混沌优化算法的优越性。文献［8］首次提出了变尺度混沌优化算法，并通过数值算例验证了所提算法的有效性。文献［9］对变尺度混沌优化算法进行了改进，并将改进后的算法应用于大规模电力系统经济负荷分配的算例中，与其他算法相比取得了更优的结果。

本文研究了变尺度混沌优化算法的初值、变量空间缩小系数、“二次搜索”调节系数对优化结果的影响，并提出了相应的改进措施，通过数值算例验证了改进措施的有效性。结合微网中微电源的特点建立了微网优化运行的数学模型，应用改进后的算法进行优化，取得了预期的效果。

1 对变尺度混沌优化算法的改进

1.1 参数的影响

变尺度混沌优化方法的具体算法步骤详见文献［8］。从理论上来讲，由于混沌变量的遍历性特点，不受初值的影响，但是迭代步数是有限的，混沌变量也就不可能遍历所有的状态，不同的初值会出现不同的结果。针对这一问题，文献［9］提出了将初值选为随机数和并行搜索的方法，但是该方法可能会使计算时间明显增加。

变量空间缩小系数和“二次搜索”调节系数选择得不恰当，可能会造成无法找到全局最优点，而只能找到局部最优的情况。同时，变量空间缩小系数和“二次搜索”调节系数的选择与目标函数有很大的关系，目标函数不变，改变缩小系数或调节系数，可以得到不同的优化结果。

1.2 算法改进

本文在文献［8-9］的基础上对变尺度混沌优化算法中变量空间缩小系数、“二次搜索”调节系数的选择进行了改进，减少了这些参数对不同目标函数优化结果的影响。

1.2.1 变量空间缩小系数的选取

在变尺度混沌优化算法中，需要根据搜索进程不断地缩小优化变量的搜索空间［8］，变量空间缩小系数就是表征优化变量的搜索空间在每次“二次搜索”过程中缩小程度的参数，本文用t来表示。

文献［8］给出了变量空间变化的公式，如式（1）所示：

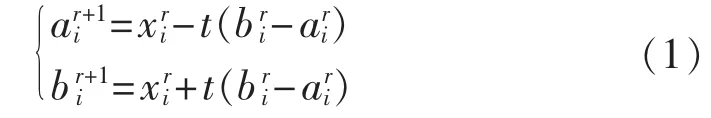
文献［8］指出 t的范围是（0，0.5），同时随着“二次搜索”次数r的不断增加，变量的搜索范围也在不断缩小。由式（1）可以看出变量的搜索空间在当前最优解附近进行调整，搜索空间的调整程度与变量搜索空间的大小有关，当搜索空间较大时，t应取较大的值，以保证搜索的速度；当搜索空间较小时，t应取较小的值，以保证搜索的精度。

为此本文提出了参数t的确定公式，如式（2）所示：

由式（2）可以看出，t的范围在（0，0.5）之间，满足文献［8］的要求。同时，随着“二次搜索”次数r的增加，变量搜索空间不断减小，t的数值也将不断减小。

1.2.2 “二次搜索”调节系数的选取

文献［8］指出在变尺度混沌优化算法中，还需要根据搜索的进程不断改变“二次搜索”调节系数。“二次搜索”调节系数是指在粗搜索得到的次优点的基础上进行微调，得到新的混沌变量，用新的混沌变量进行“二次搜索”，本文中，“二次搜索”调节系数用α表示。文献［8］给出了变尺度的公式，如式（3）所示：

由式（3）可以看出α应该是一个与“二次搜索”次数r相关的数，并且α的取值应该是一个较小的数，以保证在次优点附近进行微调。同时，随着“二次搜索”次数的增加，寻优结果不断向真值靠近，α应该不断地减小以保证寻优结果的精度。

为此本文提出了参数α的确定公式，如式（4）所示：

1.3 数值仿真

本文采用2个常用的测试函数F1、F2对算法进行测试［8-9］，所有的数值仿真和实例计算都在MATLAB中编程实现。

测试函数F1如下：

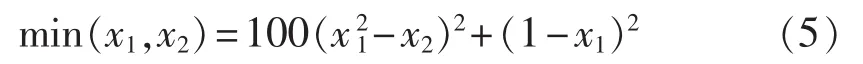
其中，变量的取值范围为：-2.048≤x1≤2.048，-2.048≤x2≤2.048。 此测试函数的理论最优解为 min（1，1）=0。

测试函数F2如下：

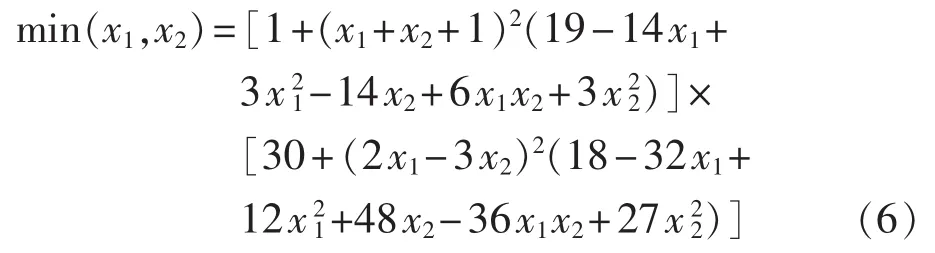
其中，变量的取值范围为：-2≤x1≤2，-2≤x2≤2。此测试函数的理论最优解为 min（0，-1）=3。

本文在进行测试的过程中，选定了相同的迭代步数，即算法耗时是一定的。表1是本文算法和文献［8］算法的对比结果。

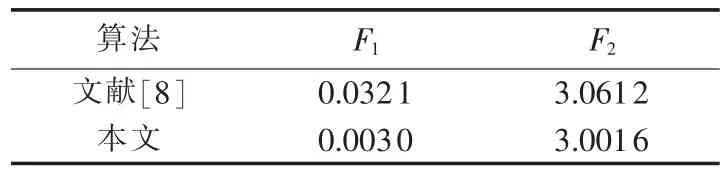
表1 本文算法与文献［8］对比结果Tab.1 Comparison of results between proposed algorithm and algorithm in paper［8］

由表1可以看出本文所选取的变量空间缩小系数t、“二次搜索”调节系数α，在迭代步数一定的情况下，能够得到更优的解，证明了本文算法的寻优效果更好。

1.4 实例验证

以文献［7］中的3机6母线系统为例，总负荷为500 MW，不考虑阀点效应和网损的情况下，惩罚因子选为10，在机组之间进行负荷的优化分配。各单元机组的参数如表2所示。本文算法运行3次得到的可行解，与文献［7］、文献［8］中算法的结果进行比较，如表3所示。由表3可见，本文算法得到的负荷分配结果比文献［7］和文献［8］的算法得到的结果费用更低，证明了本文算法的有效性。

表2 单元机组参数Tab.2 Data of units

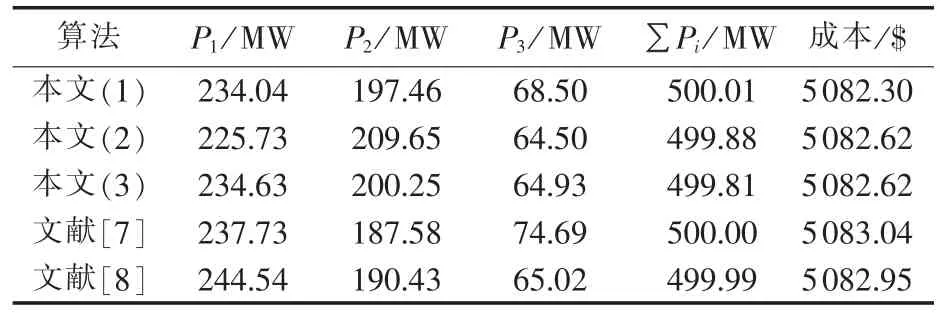
表3 本文算法与其他算法结果的比较Tab.3 Comparison of results between proposed algorithm and other algorithms

2 微网优化运行的数学模型

2.1 微网参数

本文采用简化的微网模型，该微网共有10个节点，具体结构如图1所示。微电源有微型燃气轮机（MTG）、柴油发电机（DEG）、蓄电池（BAT）、光伏电池（PV）、超级电容器（SC）。其中PV和SC的输出功率作为已知量处理，不作为优化变量。PV的实际出力设定为3 kW，SC的实际出力设定为2 kW。微电源容量如下：MTG为20 kW，DEG为15 kW，BAT为15 kW，PV为5 kW，SC为5 kW。负荷容量如下：负荷1为10+j0.1 kW，负荷2为15+j0.17 kW，负荷3为7.5+j0.05 kW，负荷4为7.5+j0.08 kW。本文在做微网优化运行时，只考虑了微网孤岛运行的情况，所以设定并网节点9的功率为0。

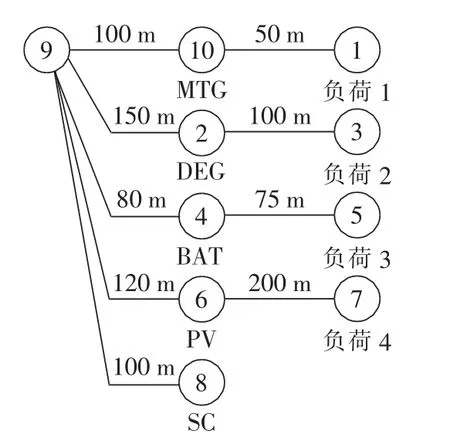
图1 微网的结构图Fig.1 Structure of microgird

2.2 目标函数

微网的优化运行是一个多目标、多约束条件的复杂优化问题［10］。本文同时考虑了微网的经济成本最小和网损最小作为目标函数，其中经济成本主要考虑了燃料成本、运行维护成本、环境折算成本。给不同的子目标函数赋予不同的权重，进行线性加权，将多目标问题转化为单目标问题，同时采用罚函数的方法对约束条件进行处理。

2.2.1 微网经济成本

2.2.1.1 燃料成本

a.MTG的燃料成本与自身的工作效率有关，表达式如式（7）所示：

其中，FMTG为MTG的燃料成本；C为MTG采用的燃料气体的单价，本文取2元/m3；VLH为天然气的低热热值，本文取9.7 kW·h/m3；PMTG为MTG的输出功率；ηMTG为MTG的效率，其大小与MTG输出功率的大小有关［11］。

b.DEG的燃料成本就是它的耗量特性函数，如式（9）所示［12］：

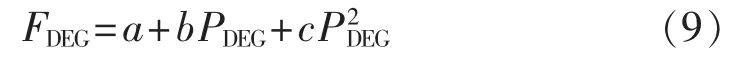
其中，参数a、b、c的大小一般由生产厂家给定，本文选取 a=6，b=0.012，c=8.5×10-4。

c.根据BAT的特性可知，BAT不消耗燃料，不存在燃料费用。

2.2.1.2 运行维护成本

微电源的运行维护成本可以用微电源输出功率乘以相关的系数来表示，如式（10）所示：

其中，E为微电源总的运行维护成本，ki为第i个微电源的运行维护成本系数，Pi为第i个微电源的输出功率，N为微电源的数目。ki的大小按照文献［12］选取，具体如式（11）所示：

2.2.1.3 环保折算成本

MTG和DEG在运行的过程中会产生氮氧化物（NOx）、二氧化硫（SO2）、二氧化碳（CO2）等空气污染物。考虑到微网的环境效益，将这些污染物按照一定的成本进行折算，作为微网优化运行的目标。具体计算公式如式（12）所示：

其中，C1为微网的环保折算成本，Pi为第i个微电源的输出功率，N为微电源的数目，aij为第i个微电源排放的第j种污染物的量，q为污染物的种类，cj为第j种污染物的折算成本。

不同种类的污染物折算成本以及MTG、DEG的排放因子如表4所示［13］。蓄电池由于其自身的运行特性，不产生污染物。

表4 折算成本和排放因子Tab.4 Conversion cost and discharge factor

综合考虑以上因素，微网的经济成本如式（13）所示：

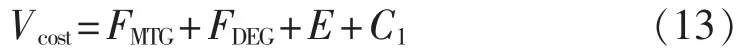
其中，Vcost表示微网的经济成本。

2.2.2 网损

由于微网一般都接在电压等级较低的配电网中，而配电网中R/X的值一般较大，在5到几十之间［14］，因此微网中传输线的网损比传统大电网的网损明显加大，不可忽略不计。网损通过潮流计算的方法得到，如式（14）所示：

其中，Pk、Qk为第k条支路传输的有功、无功功率，M为支路总数，Rk为支路k电阻，为支路电压幅值。

2.3 约束条件

功率平衡约束：

其中，Pi为第i个微电源输出的功率，N为微电源的数目，Pload为总负荷。

微电源输出功率约束：

节点电压约束：

其中，Ui为第i个节点的电压，分别为第i个节点的电压下限和上限。

3 算例仿真

本文选取的微网电压等级为380 V，线路选择LJ-16型导线，线路阻抗为R=1.98 Ω/km，X=0.358 Ω/km［15-16］。采用本文提出的改进变尺度混沌优化算法进行计算。目标函数为 F=λ1Vcost+λ2Ploss，λ1、λ2分别为多目标的权重系数，并且满足λ1+λ2=1。

算法步骤如下。

a.初始化。输入优化变量的维数N，各个微电源的输出功率上下限bi、ai，“一次搜索”最大迭代步数，“二次搜索”最大迭代步数，权重 λ1、λ2的取值，惩罚因子等参数，并随机生成N个混沌变量。

b.一次搜索。将混沌变量映射到待优化变量的取值范围内，用混沌变量进行搜索。

c.判断“一次搜索”迭代步数是否满足“一次搜索”的最大迭代步数。若不满足则继续迭代搜索，若满足则进行步骤d。

d.变尺度。对“一次搜索”得到的当前最优解进行变尺度得到新的优化变量，并调整各变量的搜索空间。

e.二次搜索。用新的混沌变量在调整后的搜索空间内执行步骤b、c。

f.重复执行步骤 d、e。

g.判断“二次搜索”迭代步数是否满足“二次搜索”的最大迭代步数。若不满足则继续迭代搜索，若满足则输出微网优化运行结果。

对λ1、λ2赋予不同的值，计算结果如表5所示。

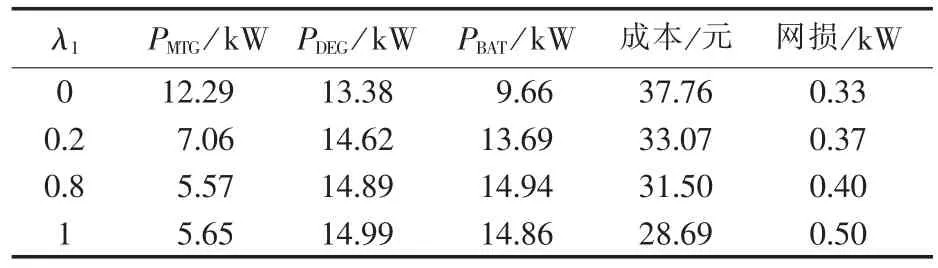
表5 权重不同时的微电源出力情况Tab.5 Outputs of micro-sources for different weight coefficients

由表5的结果可以看出，考虑不同的权重，将得到不同的优化结果，各个微电源的输出功率也不同。在进行微网的优化运行时，应结合不同用户的需要，综合考虑不同的影响因素。

4 结论

本文对变尺度混沌优化算法进行了改进，并利用典型的数值算例进行了验证，证明了改进的有效性。将该方法应用到电力系统负荷优化分配中，取得了比传统的变尺度混沌优化算法更好的效果。

本文考虑了微网的燃料费用、运行维护费用、环保折算费用和网损多个优化目标，构建了微网优化运行的多目标函数。在满足系统约束条件的前提下，采用本文所提出的改进变尺度混沌优化算法对微网中微电源的优化运行进行了分析，为进一步研究微网中微电源的有效管理提供了理论依据。