考虑空气流场影响的电缆散热研究及其影响因素与经济性分析
杨永明 ,程 鹏 ,陈 俊 ,杨 帆 ,刘行谋
(1.重庆大学 输配电装备及系统安全与新技术国家重点实验室,重庆 400044;2.重庆市电力公司电网检修分公司,重庆 400015)
0 引言
随着经济建设的飞速发展,城市供电网络越来越多地采用地下电缆。在电缆各种敷设方式中,电缆沟敷设方式具有投资省、占地少、走向灵活且能容纳较多电缆、不需要工井、电缆进出方便等优点,因此被广泛使用[1-2]。
电缆载流量是地下电缆运行中的重要参数之一,而其与缆芯温度有关。因此,准确计算地下电缆的温度场分布,对提高电缆利用率和确保电缆安全、可靠、经济运行具有重要意义[3-5]。电缆温度场的计算方法主要有2种:一种是根据IEC60287标准的解析法;另一种是数值计算法,主要包括边界元法[6]、有限差分法[7]、有限容积法[8]以及有限元法[9-10]等。 相比解析法,数值法具有运算灵活、模拟复杂工况、拓宽实验研究的范围、减少实验的工作量等优点。因此,数值法成为了研究电缆散热问题的有效手段[11]。
电缆沟内电缆的散热包括热传导、电缆表面与沟壁表面间的辐射和空气受热而形成的自然对流3种方式,其中主要是自然对流散热。而电缆沟尺寸和电缆层间距参数对沟内空气流场具有重要影响,因此,本文首先根据传热学理论[12-13],建立了考虑流场影响的电缆温度场计算模型,分析确定了其边界条件,并以电缆沟敷设6回路电缆为例验证了考虑空气自然对流(初始速度u=0)影响模型的准确性,该模型可以用于将来可能安装通风装置的电缆沟(隧道)敷设电缆的温度场计算,此时初始速度u>0。根据求得的电缆温度场分布,利用数值迭代法可得电缆允许载流量。此外,本文还对电缆载流量影响因素与考虑土建成本情况下电缆沟敷设电缆的经济性进行了分析。
1 温度场计算模型的建立
1.1 物理模型的建立
由传热学理论[12-13]中相关的知识可知,电缆沟敷设电缆的散热方式包括热传导、热对流、热辐射3种,其中自然对流散热能力要比传导和辐射大,且它们之间是流场与温度场相互耦合的过程。由于电缆沟线路与其截面尺寸相比可认为无限大,因此电缆沟内流场和温度场可以按二维进行分析和计算。本文以6回路电力电缆敷设于截面为1 m×1 m的电缆沟内为例,对电缆区域建立了一个闭域场模型,见图1。
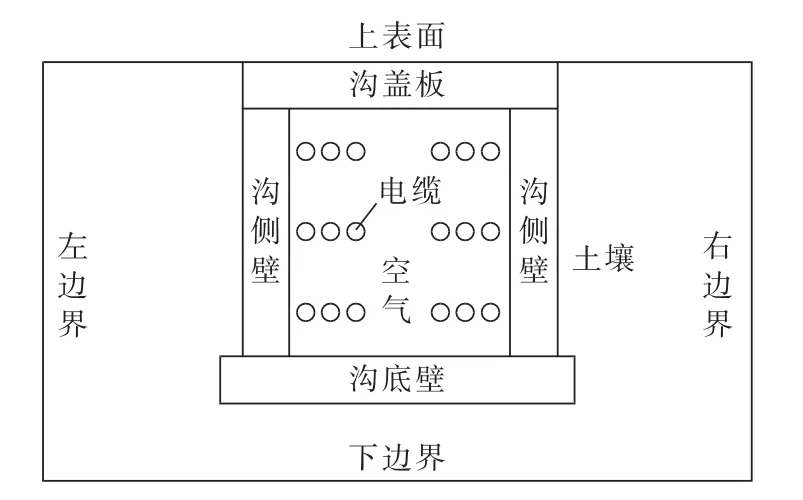
图1 6回路电缆的电缆沟敷设示意图Fig.1 Laying map of six-loop cable trench
1.2 温度场数学模型的建立
a.对流微分方程。
任何流体的流动要受物理守恒定律的支配,流动过程可以用微元体内的质量守恒定律、动量守恒定律及能量守恒定律描述[12-13]。这些守恒定律的控制方程可以写成如下形式:
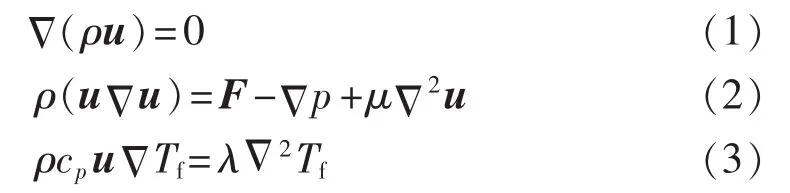
对于自然对流散热方式,空气流体所受的外力仅为重力和浮力,它们为空气流动的动力,则动量守恒方程式(2)中的F在x、y方向上的分量分别为:
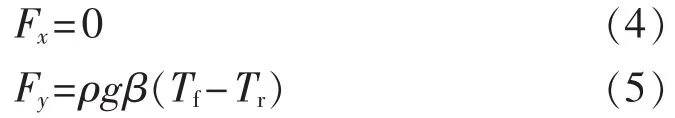
其中,g为重力加速度(m/s2);β为体积膨胀系数(K-1);Tr为流体参考温度(K)。
b.导热微分方程。
导热微分方程是根据传热学中傅里叶基本定律和能量守恒定律确定的[13]。二维导热微分方程为:
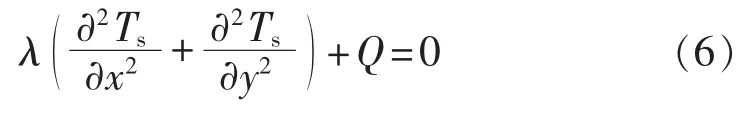
其中,λ 为介质导热系数(W/(m·K));Ts为介质温度(K);Q 为介质单位体积发热率(J/m3)。
c.辐射换热计算。
电缆外表面和电缆沟内壁之间存在辐射换热,其计算公式为:
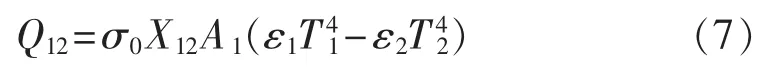
其中,Q12为表面1和2之间的净换热量(W);σ0为斯蒂芬-玻尔兹曼常数(W/(m2·K4));ε1和 ε2分别为表面1和2的发射率;X12为角系数,其值计算见文献[13-14];A1为表面 1 的面积(m2);T1和 T2为表面 1和2的绝对温度值(K)。
2 电缆温度场及载流量计算
以型号为8.7/15 kV YJV 1×400的XLPE电力电缆为例,当电缆按图1敷设时,利用有限元法计算电缆及其周围敷设区域的温度场分布,并利用数值迭代法计算电缆相应的允许载流量。
2.1 电缆结构参数及敷设条件
8.7 /15 kV YJV 1×400 XLPE电力电缆的结构参数如表1所示,具体的敷设参数见表2。
2.2 损耗计算
由式(6)可以看出:要计算电缆的温度场分布,还需获得场域内热源的单位体积发热率。对于整个电缆温度场域,只有电缆包含热源,而电缆的热源包括导体损耗、绝缘层介质损耗以及金属屏蔽层损耗和铠装层损耗等,这些参数可以根据IEC60287标准进行计算[15-17]。

表1 电缆结构参数Tab.1 Structural parameters of cable
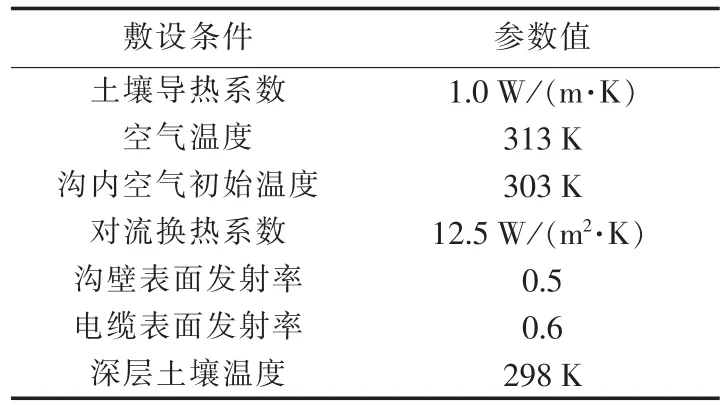
表2 电缆敷设参数Tab.2 Laying parameters of cable
2.3 边界条件
a.流场边界条件。
电缆沟内自然对流形成的流场的边界条件为:电缆沟内壁和电缆外表面为无滑移边界条件,即速度为0 m/s。
b.温度场边界条件。
传热问题中常见边界条件的控制方程为:
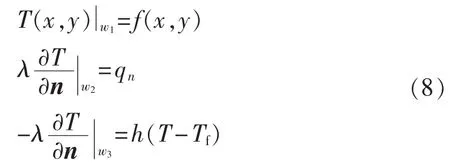
其中,T(x,y)为位于边界 w1上的点(x,y)的温度(K);f(x,y)为已知边界面上随位置变化的温度函数;λ为导热系数(W/(m·K));n 为边界法向量;qn为热流密度(W/m2);h 为对流换热系数(W/(m2·K));Tf为流体温度(K);w1、w2、w3分别为第 1、第 2 和第 3 类积分边界。
现有研究成果[4-18]表明,电缆对1.2 m外土壤的温度基本没有影响。因此,取距离电缆沟下侧1.2 m的水平直线为下边界,其边界条件为土壤深层温度,符合第1类边界条件;取距离电缆沟外侧1.2 m的2条垂直直线为左右边界,其边界条件的水平温度梯度为0,符合第2类边界条件;取地表为上边界,其边界条件的对流换热系数和空气温度已知,符合第3类边界条件。
2.4 温度场计算
用COMSOL Multiphysics软件建立电缆沟敷设电缆的几何模型,并根据计算得到的损耗参数及相关参数设置好各求解域控制方程和相应的边界条件,采用三角形单元自动网格划分法对整个求解区域进行剖分,网格剖分图如图2所示。
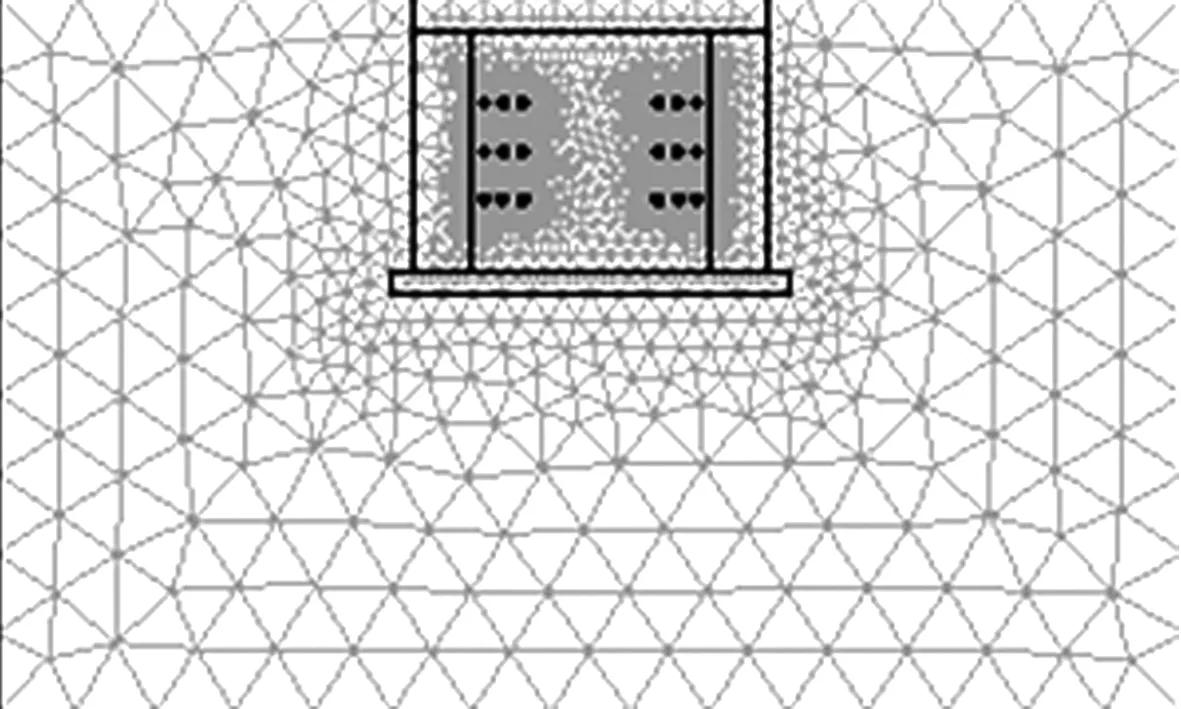
图2 求解域剖分图Fig.2 Mesh of solution region
当电缆负载电流i=250 A时,整个电缆区域温度场分布如图3所示。由图可知,此时电缆的最高运行温度为342.501 K。

图3 电缆温度场分布Fig.3 Temperature field distribution of cables
2.5 载流量计算
电缆载流量是由电缆缆芯温度确定的,准确计算电缆缆芯温度具有重要意义。当电缆缆芯温度达到363 K时的电流值即为在规定敷设条件下此种电缆的允许载流量。采用双点弦截法[18-19]得到电缆缆芯温度为90℃时的允许载流量为319.7 A。
3 载流量影响因素分析
地下电缆温度场分布的影响因素很多,敷设条件和外界环境等因素的改变都会使得电缆温度场分布发生变化。对于电缆沟敷设电缆,温度场分布受沟内空气流场的影响,而电缆沟尺寸和电缆层间距又会对沟内流场产生影响,现仍以电缆沟敷设6回路型号为8.7/15kVYJV1×400的XLPE电力电缆为例,分析电缆沟深度和电缆层间距2个因素对电缆载流量的影响规律。
3.1 电缆沟深度的影响
电缆沟深度对电缆沟内空气流场和电缆温度场具有重要影响。当电缆沟宽度和电缆层间距一定时,电缆沟深度越深,电缆沟的空间越大,电缆沟内空气的自然对流能力越强,电缆的散热能力也越强,缆芯温度降低,电缆载流量随之增大。保持电缆沟宽度为1 m和电缆层间距为0.2 m不变,电缆沟深度与电缆载流量的对应关系曲线如图4所示。由图可知,在其他敷设参数不变的情况下,电缆载流量随着电缆沟深度的增加而增大,且增大的幅度变大。当电缆沟深度由0.8 m增加到0.9 m时,电缆载流量由318 A增大到318.8 A;当电缆沟深度由1.1 m增加到1.2 m时,电缆载流量由320.7 A增大到321.9 A。
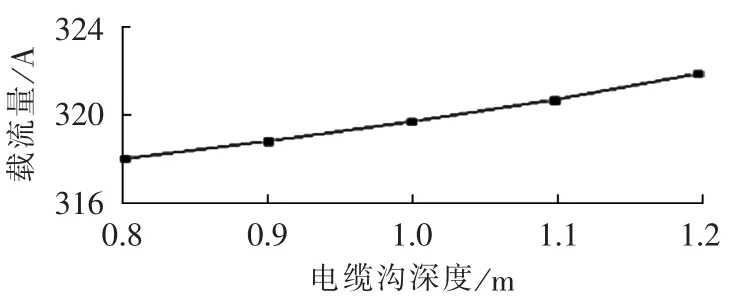
图4 电缆沟深度与电缆载流量的关系Fig.4 Relationship between trench depth and cable current carrying capacity
3.2 电缆层间距的影响
电缆层间距对电缆沟内空气流场和电缆温度场也具有重要影响。在电缆沟尺寸一定的条件下,当电缆层间距增加时,电缆之间的相互热效应减弱,同时电缆层间空气的自然对流能力增强,电缆散热能力增强,缆芯温度随之降低,从而电缆的载流量增大。保持电缆沟截面尺寸为1 m×1 m不变,电缆层间距与电缆载流量的对应关系曲线如图5所示。图5显示了在电缆沟尺寸一定的情况下,电缆载流量随电缆层间距增加的变化趋势。可以得出以下结论:在其他敷设参数不变的情况下,电缆载流量随着电缆层间距的增加而增大,且增大的幅度减小。当电缆层间距由0.2 m增加到0.25 m时,电缆载流量由321.9 A增大到324.9 A;当电缆层间距由0.35 m增加到0.4 m时,电缆载流量由329.7 A增大到331.8 A。
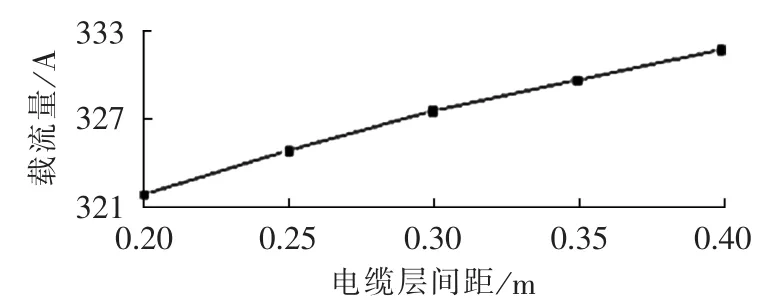
图5 电缆层间距与电缆载流量的关系Fig.5 Relationship between cable layer spacing and cable current carrying capacity
3.3 层间距变化的电缆沟深度的影响
当上层电缆到电缆沟盖板距离和下层电缆到电缆沟底距离一定时,电缆沟深度变大,电缆层间距随之增大,电缆沟内空气自然对流散热能力越强,使缆芯温度降低,电缆载流量增大。保持上层电缆到电缆沟盖板距离和下层电缆到电缆沟底距离为0.2 m不变,电缆层间距变化的电缆沟深度与电缆载流量的对应关系曲线如图6所示。由图6可知,此时的电缆载流量随电缆沟深度增加而增大,且增大的幅度减小。当电缆沟深度由0.8 m增加到0.9 m时,电缆载流量由318 A增大到322.1 A;当电缆沟深度由1.1 m增大到1.2 m时,电缆载流量由328.8 A增大到331.8 A。图6和图4对比也可以验证电缆层间距的增加有利于增大电缆载流量。
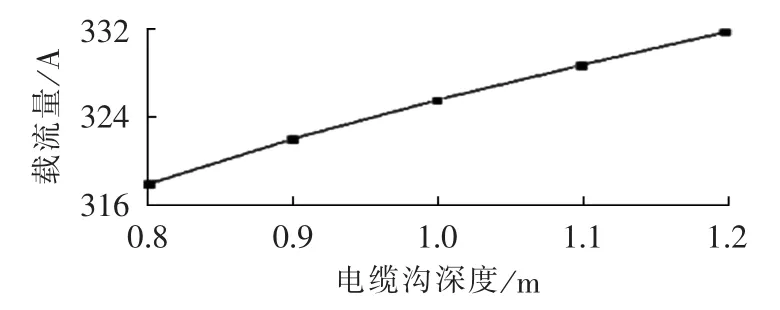
图6 电缆层间距变化的电缆沟深度与电缆载流量的关系Fig.6 Relationship between trench depth and cable current carrying capacity when cable layer spacing varies
对上述载流量影响规律进行综合分析可知,电缆沟深度和电缆层间距的增加均能够增大电缆允许载流量,但载流量相对增量的大小有所不同。将电缆沟深度、电缆层间距和电缆层间距变化的电缆沟深度与电缆载流量的关系按载流量的相对增量进行折算,即分别计算此3种不同优化类别下电缆沟深度或电缆层间距每增加10 cm对应的电缆载流量增量。得到对应于电缆沟深度类别、电缆层间距类别、电缆层间距变化的电缆沟深度类别的载流量相对增量分别为 1、5、3.5 A/dm。
可见,在改善电缆沟敷设电缆的散热效果和提高电缆载流量方面,增加电缆层间距比增大电缆沟深度能获得更加理想的效果。
4 经济性分析
随着电力工程造价的日益攀升,如何有效地控制工程造价,逐渐成为各电力企业不得不面临的问题。因此,在满足提高电缆输送容量要求的基础上,必须通过经济性分析选择最优敷设方案,最大限度地降低成本、节约资源。
虽然电缆沟深度的加深会增加电缆载流量,提高电缆利用率,但同时也会增加电缆沟的土建成本。本文根据重庆地区的挖沟土建成本情况,以1000 m、2000 m和5000 m长度的电缆沟为例分别对其经济性进行分析。根据重庆电网建设成本,重庆地区挖沟土建成本取为70元/m3,功率因数取为0.8,并取售电利润为0.1元/(kW·h),下面以电缆沟敷设6回路型号为8.7/15 kV YJV 1×400的XLPE电力电缆为例,当电缆沟宽度为1 m保持不变,电缆沟深度由0.8 m增加到1.2 m时,分析了3种不同长度电缆沟增加的土建成本的回收情况,结果如表3所示。
由表3可以看出,对于5000m长的线路1a内就可以回收建设成本,因此这种方式的经济性适合现场应用。在实际的电缆增容改造工程中,需要根据电缆线路的长度以及不同地区电缆运行维护成本,选择相应的提高载流量的方式。

表3 不同长度下电缆沟成本回收情况Tab.3 Cost recovery for different cable trench lengths
5 结语
a.电缆沟深度和电缆层间距增大,电缆允许载流量也随之增加,但电缆层间距下的电缆载流量相对增量比电缆沟深度下的值大,即在改善电缆散热效果和提高电缆载流量方面,电缆层间距优化比电缆沟深度的优化效果更佳。
b.通过电缆沟深度的优化来提高电缆载流量,虽然会使得电缆沟的土建成本增加,但是资本回收时间短,经济效益高。
c.对电缆沟敷设方案的选取应遵循的原则为:首先考虑通过电缆层间距的优化来提高电缆允许载流量,其次再考虑电缆层间距与电缆沟深度的综合优化。这对实际电缆沟敷设电缆的优化具有理论指导意义。
d.本文考虑电缆沟内空气自然对流(初始速度u=0)的电缆温度场计算模型可用于将来可能安装通风装置(初始速度u>0)的电缆沟(隧道)的温度场及电缆允许载流量的计算。

