基于web考试系统的智能组卷算法的研究与实现

杨 洁，郭喜凤，冯贵良

（河北北方学院信息科学与工程学院，河北 张家口 075000）

1 引 言

考试是教学活动中必不可少的一个环节，通过考试可以检验学生掌握知识的情况。随着计算机技术的发展以及网络的普及，对传统的教学方式产生了根本性的变革。很多课程已经开始采用在线考试方式，很多出卷方式也由计算机自动完成代替教师手工组卷。衡量一个考试系统最重要的标准就是其自动组卷算法的好坏。合理的组卷算法能够按一定要求由计算机自动从题库中选择题目，组合成一套覆盖全部知识点范围、难易适中、符合要求题量和分值等约束条件的试卷。

试卷质量的好坏直接影响考试成绩是否能反映学生的学习成果。在线考试系统中组卷算法是决定组卷质量的核心因素，组卷质量决定了试卷的质量。因此，组卷算法的性能是本文所要讨论的内容。

2 组卷算法概述

目前国内外考试系统种类繁多，常用的组卷算法有以下四种：

2.1 随机抽取算法

这种算法基本思想主要采取两种随机策略，一种是由计算机随机抽取，满足条件的试题放入试题库，此过程不断重复，直到组卷完毕为止。另一种是根据既定的指标，随机从试题库中寻找试题和指标比较，符合的放入试卷中，不符合的则放弃，重新抽取试题，如此循环，直到组卷完毕或者宣告此次组卷失败［1］。该方法实现简单，对于单道题的抽取运行速度较快，应用广泛。但是对于整个组卷过程来说组卷成功率低，只能寻找满足约束条件的题目，没有优化试卷的功能。尤其是当题库中各类型平均出题量较低时，组卷往往以失败而告终。

2.2 基于项目反映的自动组卷算法

这种算法是由适用性测试方法发展而来的，该方法的思想是尽可能的选择符合被测试者实际水平的试题。该自动组卷算法需要先评估被测试者的能力，在组卷过程中按照能力约束条件找出符合其平均能力的试题，然后通过循环修正试题的总体难度以达到最终的测试目的。该方法在实践运用中由于教师水平不同，试题库范围不同，很难确定各种试题的难度和分值等属性，不能得到一个标准的约束条件，使得组卷的成功率下降。

2.3 回溯试探法

该算法是对随机抽取算法的改进，是以深度优先的方式搜索问题解的过程。根据事先约定的约束条件随机的在试题库中抽取试题进行取舍。回溯选取法把产生的每一个状态类型纪录下来，当搜索失败时释放上次纪录的状态类型，然后再重新进行试探，通过不断的回溯试探直到试卷生成完毕或退回出发点为止［2］。当试卷题量和试题库规模比较小时，该算法效率较高，避免了随机抽取法的盲目性，组卷成功率较高。但是如果试题库比较大，回溯试探法可能会进行多次无效的试探，导致组卷时间过长，而且该算法选取的试题缺乏随机性，不能作为理想的智能组卷算法。

2.4 遗传算法

遗传算法是一种并行的、能够有效优化的算法。它从解释自然界中生物的进化论入手，模拟达尔文的自然进化模型，从代表问题潜在解集的一个种群开始，按照优胜略汰的原则，逐步演化出更好的最优解［3］。运用遗传算法，需要在每代通过适应度挑选最优个体，然后通过选择、交叉、变异、迁移等操作进行不断的所谓 “生存选择”，最后收敛到一个最适应约束条件的个体上，产生出最接近问题的解。遗传算法逐渐被用于求解最优化的问题中，该算法容错性强，搜索空间没有特殊要求，适用范围广。但在进化过程中容易陷入局部最优解，发生 “早熟”现象。

3 组卷建模

3.1 试题属性约束

组卷工作要考虑多方面的因素：要覆盖教学大纲覆盖的知识点，明确考试目标，试题的数量和题型分布。同时，题库中的每个试题都由属性值约束。根据教育测量理论，试题的属性约束包括：难度 （D）、区分度 （Q）、知识点 （K）、题型 （TY）、认知度 （S）、章节 （U）、时间 （T）。其中，影响试题质量的主要因素是试题难度和区分度。

试题的难度就是被测试者对该试题的失分率。难度系数用公式表达如下：

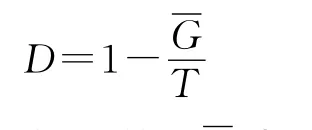
其中，D表示试题的难度系数，T表示该题的分值，表示被测试者在该题目的平均得分。从上式可以看出，平均分越大，该题目的难度系数越小。当平均分为满分时，难度系数为0，当平均分为0时，难度系数为1，难度系数的取值范围为：0≤D≤1。

试题的区分度是为了区分被测试者掌握知识水平的高低。高区分度的题目，如果被测试者能回答正确，说明水平就高，反之说明水平不高。根据研究，区分度的估算方法是：将学生按题目的得分成绩排序，将排名前25%的平均成绩记为H，排名后25%的平均成绩记为L，F记为该题目的总成绩，则区分度用Q表示为：

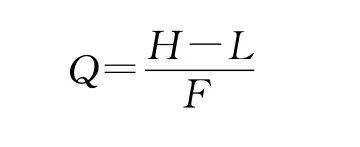
当区分度高于0.5时，认为该题目区分度很好；低于0.2时该区分度较差，该题目不能使用；区分度位于二者之间则认为区分度一般，需要改进题目质量。

作为试卷的评分指标，试题难度D越大，试题区分度就越小。当D＝0.5时，区分度Q最大，说明试题分数分布比较广泛。

3.2 组卷问题数学模型

智能组卷的数学模型相当于是一个多目标和多约束条件组合的优化问题。根据以上约束条件，可以将试卷题目做一个二维矩阵：

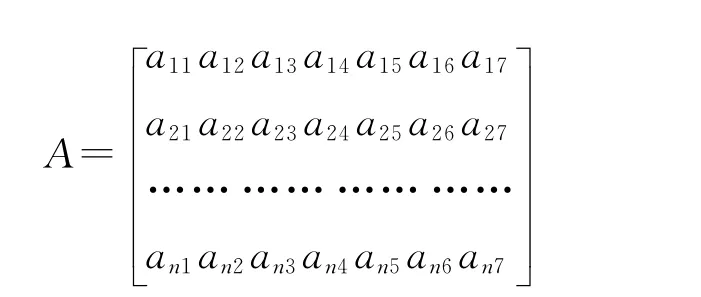
其中，n为试题总量，每一行代表一个试题，每一列都是该题目的属性约束。目标函数是将多个目标依照各自权重组合成单一目标来优化处理以期找到问题的近似最优解。故能否成功组卷就是在一个试题库A＝ ｛a1，a2，…，an｝中能否找到一个接满足试卷的所有约束条件，其目标函数为：

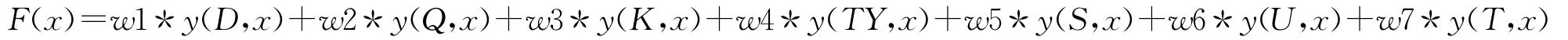
其中，权重w1＋w2＋…＋w7＝1。

4 基于分层遗传算法的实现

在传统遗传算法中，因为种族多样性过早丧失，交叉操作的搜索能力减弱，当种族出现过早收敛时，很难有效的增加种群多样性，会导致早熟现象发生［4］。为了保持种群的多样性，我们采用分层次种群协同进化的策略。该策略就是随机生成多个种群，每个种群有多个个体，种群独立操作，隔多代之后，各种群再进行迁移操作以保持种群的多样性，这样可以得到质量更高的解。该算法和一般的遗传算法类似，只是在初始种群的时候进行了分化处理，生成多个子种群，这样，每个子种群有各自的样本，可以得到更优的结果，自适用度更高。

分层次的遗传算法主要由编码、选择、交叉和变异组成［5］。

4.1 编码

在求解过程中将问题进行编码主要是为了提高搜索性能。已有大量数据表明，在多约束条件下，采用整数编码的遗传算法效率较高，因此，本算法中采用整数编码的方式。将每套试卷的结果映射到一个染色体上，即一个试题代表一个染色体基因。根据试题的类型设置段数，每段编码的基因个数正好等于该类型试题库中的序号。同时，染色体采用长编码策略处理，染色体中的基因个数即为试卷中试题的总数，且题型间的编码方式是独立的。

4.2 选择

改进的遗传算法的选择操作在子种群内部进行，根据其平均适应度对子种群进行选择。其中，适应度高的子种群被选择进入下一次迭代过程，反之则被淘汰。

4.3 交叉算子

该算法的交叉不仅是种群内部的交叉，子种群间和子种群内也同时进行交叉。种群内部进行交叉操作后，两子种群间也要进行段间交叉算子的方法。完成交换后子种群数增加一倍，为了保证种群数目的不变，在做交叉算子的两种群间进行适应度比较，适应度较大的保留，反之淘汰。

4.4 变异算子

因为变异算子是有小概率事件产生的，为了提高搜索速度在改进算法中采用单点变异算子。随机选取一个染色体，然后生成0-1的随机数r，当r小于其变异概率则在每段随机生成一个变异点，即在该类题型段中随机选取一个未被选中的题目并标记为选中，同时该题置换成未选中，反之不进行变异操作。

5 数据分析

下表1为传统遗传算法和改进后的算法在考试系统中组卷成功率数据的对比，其中1表示传统算法，2表示改进后的遗传算法：

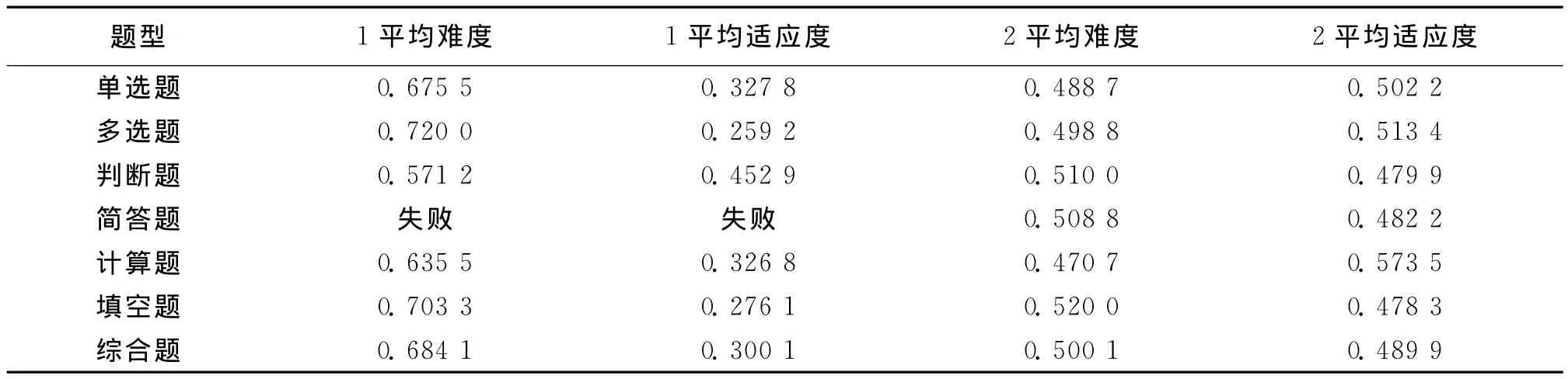
表1 个题型平均约束条件对比

通过以上数据表明，实际应用中遗传算法中易出现收敛速度慢、稳定性差、易早熟的特点。通过修改遗传算法中的算子以及对适应度函数进行尺度变化可以避免早熟现象的发生。但在单种群基础上的改进只能控制个体进化，很难达到理想结果，选择多种群进化可以改善遗传算法的全局收敛性，控制早熟度。改进的遗传算法在全局搜索性能和收敛速度上都有明显的优势，组卷质量较高。能够满足实际的需求。

6 总 结

随着计算机技术的发展和普及，计算机辅助教学已经作为一门新的教学方式越来越受到广大教育工作者的关注。智能组卷作为计算机辅助教学的核心也是大家关注的焦点。组卷算法是评价一个组卷好坏的重要因素［6］。

分层次的遗传算法由于种群的多样性，提高了局部收敛度和全局的搜索能力，基于该算法的自动组卷系统组卷质量高，知识点分布均匀，试题难易适中，降低了试卷的重复率，同时降低了人工组卷中由于人为因素所造成的失误。真正实现了教考分离和考务自动化。

［1］路平，王敏娟，万昆.试题库自动组卷策略研究［J］.电脑开发与应用，2001，14（02）：9-11.

［2］王宇颖，侯爽，郭茂祖.题库系统市局自动生成算法研究［J］.哈尔滨工业大学学报，2003，35（03）：342-346.

［3］赵忠平，杨浩.智能组卷系统的设计与实现［J］.山西师范大学学报：自然科学版，2008，22（02）：28-32.

［4］苏小红，杨博，王亚东.基于进化稳定策略的遗传算法［J］.软件学报，2003，14（11）：1863-1868.

［5］刘彬等.智能组卷系统试题库结构的研究［J］.信息技术，2002，3（07）：2-4.

［6］刘树刚.一种 web测试中的组卷策略及其改进［J］.烟台大学学报，2004，17（01）：59-64.