罗茨风机转子系统动态特性分析

吴国帅， 王 栋

(西北工业大学航空学院，陕西 西安 710072)

0 引言

罗茨鼓风机是一种使用范围很广的机械设备，被广泛使用于污水处理、电力、化工及水产养殖等领域，作为一种重要的工业设备，它的主要做功部件是一对具有两叶或三叶的转子系统[1]。转子系统作为罗茨风机最主要的工作部件，由于设计不合理、材料质地不均匀、加工组装误差以及运行过程中集灰、磨损等原因使转子在运行过程中产生不平衡力，导致转子中心惯性力偏离其旋转中轴线，这样机器在运转时会出现附加惯性力，通过轴承传递到整个风机箱体上。不平衡力的出现会给机器带来振动以及噪声，降低轴承零部件的寿命。因此，转子系统的平衡性的好坏是决定罗茨风机振动强弱的重要因素[2]。罗茨鼓风机结构复杂，形式多样，振动耦合严重，如果转子系统的固有频率和风机箱体的频率一致或相近，会使箱体组件产生共振，加剧风机振动，产生更大的噪声，所以风机转子系统的振动已经成为阻碍风机提高性能、稳定性和安全性的重要因素[2]。罗茨风机转子系统在工作中主要承受转子不平衡力、齿轮啮合力、叶轮啮合冲击力等的作用，转子在旋转过程中产生周期性的扭转应力和弯曲应力，使转子在工作过程中既弯曲又扭转，出现疲劳损伤，附带的也会影响其它部件的正常运转。所以只要获取转子系统的应力、应变以及模态参数，就能对设计出好的转子提供积极的参考作用。有限元法在振动方面已经有了一定的研究，如谭青等[3]对离心式鼓风机转子采用集中参数法建模，利用传递矩阵法编程求解转子不平衡响应，并提出一种基于振型分析的最大值估算法;钱网生[4]使用降噪结构设计和模态实验技术相结合的方法，来降低空调风机的振动噪声。

现有文献关于罗茨风机转子系统动态特性研究较少，本文以某罗茨风机转子为例，建立有限元结构模型，用有限元分析软件ANSYS研究其动态特性。通过本文研究，可以得到转子系统的模态参数、谐响应特性，了解转子系统的振动频率、振动形式和振动强弱，并可以在风机设计之初，预估风机系统的振动特性，为改善风机系统的动态性能提供理论依据。

1 转子系统模型建立

某罗茨风机建模的主要尺寸有:转子系统总长605 mm，三叶轮型线为渐开线，叶轮最大宽度59 mm，叶峰到叶轮中心的距离为87 mm，三叶轮两端中心空腔直径32 mm，长41 mm，三叶轮中心空腔直径42 mm，叶轮中心两端空腔直径45 mm，叶轮总长350 mm，叶轮轴最大直径55 mm，轴为阶梯状结构;齿轮法向模数2.5 mm，齿数48，分度圆直径120 mm，齿宽45 mm。该转子材料45钢，杨氏模量200 GPa，密度 7 800 kg/m3，泊松比 0.3。

1.1 转子系统的简化

采用Pro/E5.0绘制罗茨鼓风机转子系统三维实体结构模型，如图1所示。根据转子结构特点和计算需要，忽略了倒角、键槽等对转子刚度与质量影响不大的结构。将Pro/E5.0建立的三维模型生成符合IGES标准的接口文件，通过通用接口导入有限元软件。

1.2 转子系统有限元模型建立

网格划分采用Mesh工具划分，转子系统表面采用Workbench中Map设置，局部采用Sizing设置，叶轮部分设置10 mm，齿轮部分设置5 mm，划分中转子系统生成节点总数103 849个，单元总数61 718个，Skewness Average值0.34，网格质量好，网格划分结果如图2所示。

图1 转子系统三维实体图

图2 转子系统网格划分图

2 转子系统的动态分析

2.1 动态特性理论

结构的动态特性有两个方面的要素，包括结构部件的固有频率和固有振型。在承受动态载荷的结构中，固有振型和固有频率对于转子系统动态分析非常重要，我们可以运用模态分析来计算结构的固有振型和固有频率。对于其它动态分析如瞬态动力学分析和谐响应分析，模态分析是这些分析的起点[6]。如果能够率先获得结构的固有频率这一参数，那么我们在对结构进行设计和优化的过程中，就可以有针对性地使固有频率避开外部激励的频率，这样做的目的是要排除共振，避免结构出现较大程度的变形。

在不同阻尼条件下，机械部件上各点对外界激励的响应都可以表示成多种参数矩阵叠加，如

其中F(t)是激振力向量，M是总体质量矩阵，C是阻尼矩阵，K是刚度矩阵，U是位移向量。

运用(1)式来求解转子系统在自由振动状态下的固有频率和固有振型时，我们令F=0，也就是不考虑转子系统所受的外载荷。同时，转子系统在工作时，由于阻尼对固有振型和固有频率所产生的影响微乎其微，因此不计算阻尼项，那么此时，在无阻尼自由振动状态下，转子系统运动方程就可以简化为[6]:

出于更好理解方程解的具体意义的考虑，(2)式可以转化成简谐振动形式的方程:

随着时间变化，线性结构承受着按正弦规律变化的载荷，对于这一指标，我们可以运用谐响应分析来计算。设计人员可以得出线性结构在几种频率下的响应值对频率的曲线，继而推导出结构的持续性动力特性，从而考察设计对共振、疲劳运作等可能产生的有害后果。

系统在简谐激励载荷作用下的运动方程为[6]:

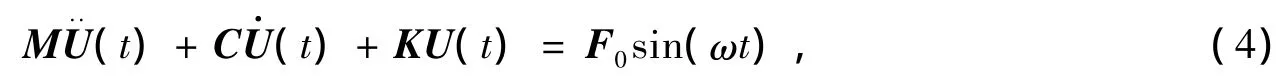
式中:F0是简谐激振载荷的幅值;ω是角频率，等于外界激振频率;M是结构的质量矩阵，K是结构的刚度矩阵，C是结构阻尼矩阵，U(t)是节点位移矩阵。

在线性系统中，(4)式可以有以下通解:

在(5)式中，U1(t)为式(4)的齐次方程通解，如果在弱阻尼条件下，存在初相角ψ，则(5)式又可以转化为

式(5)中，U2(t)为式(4)的非齐次方程的一个特解，其频率与非齐次项的正弦函数一致，存在初相角φ，则有

由此，根据(4)—(7)式推导，可以有

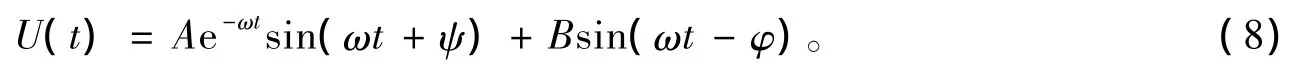
结构在简谐激励载荷下的响应是衰减状态之下有阻尼的自由振动和有阻尼的受迫振动的叠加后果。但值得注意的是，有阻尼的自由振动会随着时间推移而消逝，而有阻尼的受迫振动则会持续。由于经验和技术限制，本文只研究受外部激励的稳态受迫振动响应特性。

2.2 主被动转子受力分析

罗茨风机转子主要承受轴承传递的力、齿轮重力、齿轮传递的扭矩，其结构尺寸及受力分析如图3所示。转子质量W=20.5 kg;齿轮质量Wg=3.5 kg;罗茨风机轴功率w=20.5 kW;转子L1=L2=62 mm，L3=92.5 mm，L=470 mm;转子直径 D=135 mm;叶数 Z=3。

对被动转子受力分析，被动转子主要承受轴承传递的力矩Tg，齿轮的重力Wg以及轴承座的支撑力，左端轴承座支撑力Fax和Fay，右端轴承座支撑力为Fbx和Fby，转子系统还承受自身重力W和气体压力q，如图3所示。

被动转子在铅垂面内分别对a点和b点取矩，即得

通过受力分析得到转子所承受的轴承支撑力。左端被动转子传给机体的力Fx=148.56 N，Fy=1 538.6 N;右端 Fx=397.89 N，Fy=2 372.5 N。

3 有限元分析结果

3.1 有限元模态分析结果

图3 转子系统受力分析

计算转子系统的模态参数可以检验罗茨风机在运转过程中是否发生共振。有限元分析时，在边界条件设置时不添加任何约束以保证转子系统处于自由状态，直接计算转子系统的自由模态。罗茨风机是低转速旋转机械，因此有可能引起共振的频率是较低阶的频率。所以，在用有限元法计算模态时，只需要取转子系统的前20阶固有频率。转子系统在自由状态下计算出来的前6阶固有频率是刚体性模态，其数值可以看为零。所以只需研究后面的14阶固有频率。基于有限元法计算出转子系统前20阶模态，为了便于研究只提取前12阶非零模态。表1给出了转子系统前12阶固有频率及对应的固有振型。

表1 转子系统非刚体固有模态

从表1可以看出，转子系统的固有频率从1 327.4 Hz到4 731.2 Hz分布不等，其各阶模态对应的固有振型主要有弯曲、摆动、扭转、旋转，变形位置分布在轴端、齿轮、叶峰等位置，最大振幅高达47.93 mm。第 1，2，4，5，7，8，10，11 阶固有频率振幅较大区域主要分布在转子系统的轴端，振型主要有弯曲、摆动、扭转，频率分布在1 327.4～4 534.8 Hz，轴端振幅最大值为47.93 mm。第3和第9阶固有频率对应的固有振幅较大区域主要分布在齿轮位置，固有频率为1 962.6 Hz和4 259.7 Hz，齿轮固有振幅最大值为24.19 mm，第6和第12阶固有频率振幅较大位置在叶峰处，振幅最大值为16.34 mm，对应固有频率为2 964.5 Hz和4 731.2 Hz。在转子系统设计时要注意避开这些共振频率，减少转子系统的共振发生，在整机设计时也要把外部激励频率与这些频率值错开，减少整机的振动。

图4所示转子系统前12阶非零模态对应的固有振型。

3.2 有限元谐响应分析结果

图4 转子系统非固有频率和模态振型

基于有限元方法，对转子承受轴承传递的力、齿轮重力、气体压力、齿轮传递的扭矩的情况下研究转子振动特性，图5显示齿轮处在上述力作用下的振幅变化情况，随着振动工作频率的增加。振幅在1 500 Hz处出现极值，其中y方向振幅最大，z方向次之，x方向最小，最大值为6.5×10－3mm，最小值为1.0×10－3mm，这说明在1 500 Hz时发生共振，且y方向振动最剧烈，占振动的主要成分。图6显示叶轮处振幅随频率变化特性，随着频率的增加，叶轮振幅也出现极值，出现极值的频率为1 500 Hz，其中z方向振幅最大，y方向次之，x方向振幅最小，最大值为6.5×10－5mm，最小值为0.5×10－5mm。整体来说，齿轮附近的振幅比叶轮处振幅大的多。

图5 齿轮处幅频曲线

图6 叶轮处幅频曲线

4 结论

本文通过对罗茨风机转子系统进行有限元模态分析和谐响应分析，为以后罗茨风机的优化和改进设计提供了重要的理论参考，获得的主要结论如下:

(1)通过对转子系统有限元分析，可知其前6阶固有频率接近于零，对应转子的刚体平动，而从第7阶开始，转子系统在运转过程中，转子既弯曲又扭转。转速越高，出现危险振型的概率越大，甚至会形成扭曲。为了避免产生交变载荷，需要提高轴承的刚度。转子系统的叶轮叶峰、齿轮、两轴端处是变形较大区域，在振动过程中是危险区域。所以在转子系统设计过程中应充分考虑叶轮的设计厚度及内部空腔直径的大小及齿轮的强度和刚度、两轴端的长径比。

(2)转子系统谐响应分析显示，转子系统振幅最大位置在齿轮处，最大值为0.007 mm，所以在转子设计过程应加强齿轮的刚度。

(3)转子系统模态和谐响应分析对转子系统设计优化十分重要，所获得的固有频率、固有振型及幅频曲线能预测罗茨风机各部件之间相互干扰的可能性及振动强弱，通过合理的结构设计可以避开共振，这为罗茨风机的优化和改进设计提供了理论依据。

[1]苏春模.罗茨鼓风机及其使用[M].湖南:中南大学出版社，1999.

[2]赵引峰，王云霞.罗茨式鼓风机常见机械故障分析及处理[J].煤矿机械，2001(12):60-62.

[3]谭青，李仲阳，张怀亮.离心鼓风机转子不平衡响应计算的实践[J]风机技术，1997(4):20-23.

[4]钱网生.离心通风机低噪声设计研究[J].机电设备，1997(1):26-29.

[5]浦广益.ANSYS Workbench 12基础教程与实例详解[M].北京:中国水利水电出版社，2011.

[6]傅志方，华宏星.模态分析理论与应用[M].上海:上海交通大学出版社，2000.

[7]王旭飞，刘菊蓉，戴俊平，等.新型真空油泵活塞的有限元模态分析[J].机械设计与制造，2010(9):104-106.

[8]谭明敏，杨务滋，周立强，等.挖掘机式冲击器斗杆有限元模态分析[J].中南林业科技大学学报，2011，31(4):187-191.