基于二维压差矢量传感器的定向误差分析

李 婧，韩 鹏，刘 洋，李 杨，檀 虎

（1．西北工业大学 航海学院，陕西西安 710072;2．西北机电工程研究所，陕西咸阳 712000）

0 引言

矢量传感器作为一种可以空间共点、时间同步测得声场中声压和质点振速的传感器，为水声技术带来了新的发展。它也因为体积小、质量轻、布放方便，且具有低频指向性，适合在小型平台中应用，可以有效解决低频辐射噪声测试问题，提高拖线阵的噪声抑制能力，消除拖线阵中单次定向中的左右舷模糊，切实改善目标定向精度等优点［1，2］。

矢量传感器技术虽然在水声探测中得到广泛应用，针对矢量传感器的研究越来越多，但是主要集中在目标识别算法和阵列信号处理等方面，关于矢量传感器定向的误差分析和补偿的研究关注不足。为了能进一步了解研究矢量传感器，提高矢量传感器目标识别和定向的精度，本文针对二维压差矢量传感器水下目标定向系统［3］展开误差分析。

1 二维压差矢量传感器结构

二维压差矢量传感器可以看成一个四元的离散圆阵，它由2组互相垂直的偶极子对组成［4］，平面图如图1所示，其中4个阵元均为普通的声压水听器，偶极子对中的2个阵元要求具有相同的幅频响应。设位于坐标轴上的4个基元分别为1，2，3，4，规定x轴代表零度方向，逆时针为正，o为参考点。图中，圆周半径为r，声速为c，信号频率为f，目标的方位角为θ。

设沿x轴方向的声源信号为

图1 二维压差式矢量传感器平面图Fig 1 Planar view of two-dimensional differential pressure vector sensor

各基元的信号可以表示为

式中P0为声压幅度，k为波数，k=ω/c，c为介质声速。

2 误差分析

二维压差矢量传感器，通过相关法定向［5］，可以实现目标的精确定向，目标水平方位角与俯仰角的计算公式

由于压差矢量传感器获得的声场的声压与振速信息，是分别通过压差矢量传感器的四基元声压求声压算术平均和利用有限差分近似原理计算得出的。而实际工程应用中，压差矢量传感器四基元制作工艺的不完全一致和自身的装配误差，都会引起中心点处声压、振速的偏离，带来方位估计误差，影响定向精度，同时定向精度也受信噪比和目标方位角度影响。为了了解这些误差对目标定向精度影响的程度，提高目标定向的精度，本文结合二维压差矢量传感器定向原理，主要分析基元位置误差、基元通道不一致性及目标入射角度对定向精度的影响展开了分析。

2．1 基元位置误差建模

考虑运算量和复杂度，假设二维压差矢量传感器仅1个基元有误差，即如图2所示基元3不在以基元1，2，4组成的圆上，定义偏离为Q（a，b）。其中a表示基元离圆心的距离偏差（后均简称为基元距离偏差），b表示基元偏离x轴的夹角（后均简称为基元角度偏差）。

接收到的信号形式为

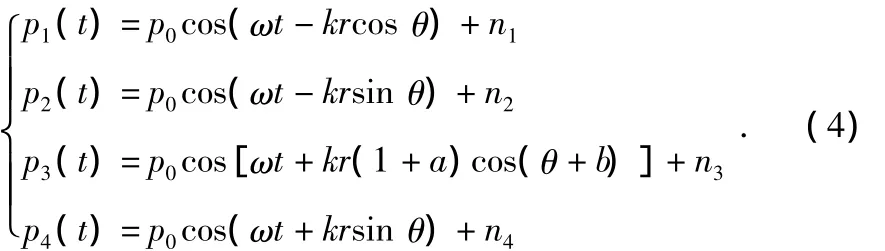
图2 存在基元位置偏差的矢量传感器示意图Fig 2 Vector sensor diagram with element position deviation

为方便分析，忽略噪声信号ni（i=1，2，3，4），利用相关法定向可得，只存在基元角度偏差时，方向估计角为

只存在基元距离偏差时，方向估计角为

当基元角度偏差和距离偏差同时存在时，方向估计角为

通过以上公式，可以计算得到存在基元位置误差［6］时目标的方位角度。

2．2 通道不一致性误差建模

压差式矢量传感器的4个声压传感器通道响应很难保持一致，而通道的不一致将导致方位估计误差。压差矢量传感器的通道不一致可分为基元幅度响应不一致和基元相位响应不一致2种。

二维压差式矢量传感器含有4个声压水听器基元，若将矢量传感器的每个基元看成是一个系统，则二维矢量传感器系统可以用图3表示。

如图3所示，压差矢量传感器四基元分别测得四路声压信息，进一步计算可得到中心点处的声压与振速信息。图中p'i（t）（i=1，2，3，4）为各基元声压真实值，Hi（w）（i=1，2，3，4）为各基元的幅度相位响应函数，pi（t）（i=1，2，3，4）为各基元输出声压值。

设响应函数为

式中ai（i=1，2，3，4）为基元幅度响应，bi（i=1，2，3，4）为基元相位响应。考虑运算量和复杂度，假设基元1，2，4幅度相位响应一致，即Hi（w）=1（i=1，2，4），基元3幅度相位响应不一致。

图3 二维压差矢量传感器系统框图Fig 3 System block diagram of 2D differential pressure vector sensor

假设目标信号为远场平面波信号，幅度响应偏差为a，相位响应偏差为b，则压差矢量传感器四基元输出信号可以表示为

忽略噪声信号ni（i=1，2，3，4），利用相关法定向可得只存在基元幅度响应偏差时方向估计角为

只存在基元相位响应偏差时，方向估计角为

当幅度和相位响应偏差同时存在时，方向估计角为

以上为压差式矢量传感器存在通道不一致性误差［7］时方位估计公式，通过公式可以得到同一水平面上目标的位置。

3 仿真分析

为了能进一步了解，位置误差与通道不一致性中，各因素对于目标方位估计影响的程度，得出主要影响因素，方便方位估计的补偿研究，将位置误差中的基元距离偏差、基元角度偏差与通道不一致性中的基元幅度响应偏离、基元相位响应偏离进行组合仿真分析［8］。

3．1 基元位置误差与通道不一致性各存在一种对方位估计的影响

假设目标入射角度为30°进行仿真可得，图4为基元相位响应偏差和基元位置距离偏差对方位估计的影响，图5为基元幅度响应偏差和基元位置距离偏差对方位估计的影响，图6为基元幅度响应偏差和基元位置角度偏差对方位估计的影响，图7为基元相位响应偏差和基元位置角度偏差对方位估计的影响。

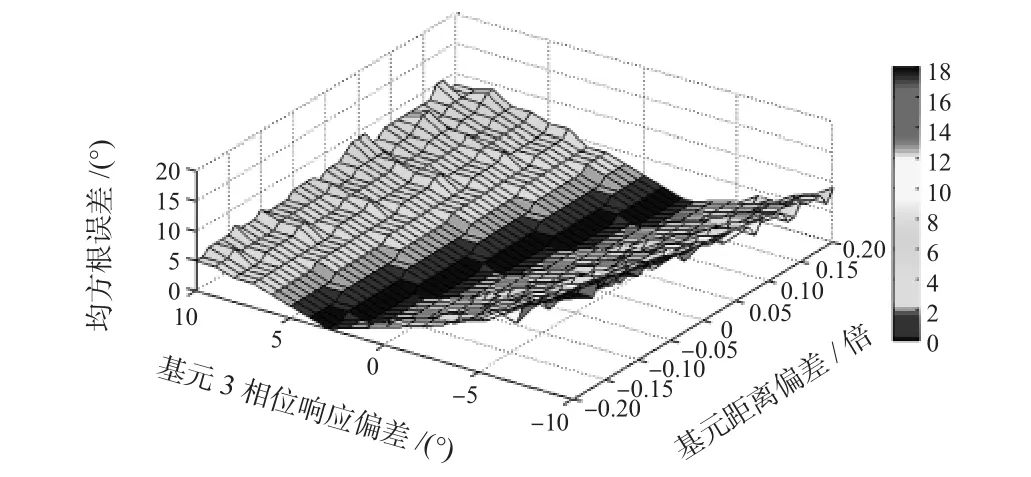
图4 基元相位响应偏差和基元位置距离偏差对方位估计的影响Fig 4 Effect of element phase response deviation and element position distance deviation on bearing estimation

图5 基元幅度响应偏差和基元位置距离偏差对方位估计的影响Fig 5 Effect of element amplitude response deviation and element position distance deviation on bearing estimation

从图4、图5可以看出:在目标方位估计中，存在基元距离偏差的情况下，若存在基元相位响应偏差或者基元幅度响应偏差，方位估计误差主要受基元相位响应偏差或基元幅度偏差的影响。如图4基元相位响应偏差为5°时，基元距离偏差为0～0．2倍时，方位估计误差变化为2°左右，而基元距离偏差为0．1倍时，基元相位响应偏差为0°～10°时，方位估计误差达到8°左右。图5中基元幅度响应一定，基元距离的变化导致误差的变化在3°左右;基元距离偏差一定时，基元幅度响应偏差达到10°，明显地影响了目标的方位估计。

图6 基元幅度响应偏差和基元位置角度偏差对方位估计的影响Fig 6 Effect of element amplitude response deviation and element position angle deviation on bearing estimation

图7 基元相位响应偏差和基元位置角度偏差对方位估计的影响Fig 7 Effect of element phase response deviation and element position angle deviation on bearing estimation

图6为同时存在基元幅度响应偏差和基元角度偏差时目标的方位估计，图7为存在基元相位响应偏差与基元角度偏差时目标的方位估计图。如图6所示，基元幅度偏差在-0．05～0．05倍以内时，基元幅度偏差与基元角度偏差共同影响目标方位估计，误差在2°以内，超出此范围误差随着基元幅度偏差的增大而迅速增大，此时，基元幅度偏差为影响方位估计的主要因素。图7表明，基元相位响应偏差在-3°～3°以内，方位估计误差在2°以内，基元相位响应偏差一定时，基元角度偏差从-10°～10°的变化引起方位角的变化小于3°，基元相位偏差对方位估计的影响明显大于基元角度偏差。因此，存在基元通道不一致性误差和基元角度偏差时，基元通道不一致性误差为影响方位估计的主要因素。

3．2 基元位置误差与通道不一致性同时存在对方位估计的影响

以上分析了存在2种情况下的方位估计误差影响情况。下面将就基元的位置误差和通道不一致性同时存在时，方位估计误差的分布进行仿真。

接下来分析基元位置误差同时存在时，通道不一致性与位置误差对方位估计的影响，假设位置误差一定，对通道不一致性对方位估计的影响进行仿真分析。

在同样的仿真条件下，假设基元位置距离偏差为0．15倍，角度偏差5°，进行仿真得到图8存在基元位置误差时基元通道不一致性对方位估计的影响。

为了进行对比，在同样的仿真条件下，只存在基元通道不一致性时，仿真得到如图9所示。

将图8与图9比较，两者变化趋势相似，说明存在基元位置误差，且误差为距离偏差0．15倍，角度偏差为5°时，通道不一致性对方位估计的影响为主要影响因素，此时可以忽略位置误差的影响。

综上所述，基元位置误差中的距离或者角度偏差与基元通道不一致性中幅度响应偏差或者相位响应偏差不论是各存在一种还是共同存在，位置误差对方位估计有一定的影响，但影响很小，方位估计误差变化趋势按通道不一致性误差的变化而变化，所以，得出通道不一致性误差为方位估计误差的主要影响因素。

图8 存在基元位置误差时基元通道不一致性对方位估计的影响Fig 8 Effect of element channel inconsistency on bearing estimation with element position deviation

图9 只存在基元通道不一致性对方位估计的影响Fig 9 Effect of only with element channel inconsistency on bearing estimation

4 结论

由以上分析可得，二维压差式矢量传感器由于基元距离偏差、角度偏差、幅度响应不一致及相位响应的不一致导致方位估计出现偏差，影响方位估计的精度。仿真分析表明:影响方位估计的因素中基元距离偏差和角度偏差对方位估计有一定影响，但不明显，而通道不一致性误差对目标的方位估计会产生较大影响。为了提高目标的方位估计的精度，后续需要对通道不一致性误差进行补偿［9］。

［1］ 杨德森，洪连进．矢量水听器原理及应用引论［M］．北京:科学出版社，2009．

［2］ 陈洪娟．矢量传感器［M］．哈尔滨:哈尔滨工程大学出版社，2006．

［3］ 张法利，赵俊渭，张银冰．基于矢量传感器的水下运动目标测向的研究［J］．舰船科学技术，2007，29（2）:72-75．

［4］ 程彬彬，杨士莪．基于二维压差式矢量水听器源估计误差分析［J］．西北工业大学学报，2006，24（6）:800-803．

［5］ 李 丹．矢量传感器水下定位技术及误差补偿的研究［D］．西安:西北工业大学，2011:25-35．

［6］ 刘伯胜，田宝晶．矢量传感器估计目标方位的误差的仿真研究［J］．哈尔滨工程大学学报，2003，24（5）:491-495．

［7］ Hawkes M，Nehora A．Acoustic vector-sensor beamforming and capon direction estimation［J］．IEEE Trans on Signal Processing，1998，46（9）:2291-2304．

［8］ Han Peng，Liu Yang．Localization technology basing two-dimensional vector sensor［J］．ICMST，2012:622-623，1384-1388．

［9］ 曾喆昭，竺 炜，王耀南．一种基于正交基神经网络算法的传感器误差补偿方法［J］．传感器技术学报，2007，20（3）:536-539．