圆弧齿轮齿面沿接触线是滚动与滑动并存的证明
康星虎,闫文斗,段建中
(宁夏大学 机械工程学院,宁夏 银川750021)
0 前言
圆弧齿轮传动在我国有较长的研究和应用历史,并掀起过热潮,也取得了较大成绩。但近些年来,国内学术界对该课题的研究趋于冷淡。本课题组在进行多圆弧齿廓齿轮的若干年持之以恒研究中,对公开或内部发行的圆弧齿轮传动的中文专著中基本理论进行了梳理,并发现了一些缺陷。本文的任务是否定圆弧齿轮经典著作[1-2]中第39~40页表述的基本观点:凹齿廓与凸齿廓之间沿接触线是纯滚动。手册[3]亦未明确解释具体运动形式。根据几何数学与运动学分析表明:凸凹齿廓啮合的一对齿轮副的两条接触线长度不相等,因此啮合点在接触线上的速度大小亦不相等,进而可知:两齿面之间沿接触线的运动必定是滚动与滑动并存。该结论的意义在于:1)明确了凸凹齿廓之间沿接触线的运动形式,2)给出了这种运动形式的定量公式,3)可以用该结论合理地解释圆弧齿轮传动中的一些物理现象:如油膜厚度大,齿面磨损均匀,跑合性良好等;并且为这些物理现象的定量分析奠定了数学与运动学基础。为了有力地论证此结论,很有必要介绍圆柱螺旋线相关知识。
1圆柱螺旋线数学表示与几何意义
由圆弧齿轮的形成原理可知[1],圆弧齿轮参与啮合时的接触线是一条圆柱螺旋线。圆柱螺旋线方程为[3]:

其中:r—螺旋线所在圆柱的半径;ψ—角度变量,0≤ψ≤θ。
圆柱螺旋线的形成过程用图1即可说明。T为圆柱上端面圆周上任意一点,M从T点开始,沿所在圆柱面母线以速度V匀速向下运动,同时圆柱以角速度ω绕轴线oo匀速旋转,那么点M在圆柱面上的轨迹就是曲线TA,则曲线TA就是圆柱螺旋线,它的长度:

图1 圆柱螺旋线

由螺旋线运动学分析可知[4]:ψ = ωt,z=Vt。则可由轴向距离Z相等得到:pψ=Vt,两边同除以时间t得到:

圆弧齿轮中的螺旋线的性质,由下面的论述给出:
如图2所示,以齿轮底面作为xy平面,将齿轮轴线作为z轴,在图2中齿轮某一齿面上有n条螺旋线A1B1,A2B2,…AnBn,它们都是以齿轮轴线为中心轴的圆柱面与螺旋齿面的交线,根据式(1)可得到其参数方程为:

图2 螺旋线性质说明图

其中:r1=OA1,r2=OA2,…rn=OAn。现有一垂直于齿轮轴线的平面S,它与螺旋线的交点分别为,…,与齿面的交线为一段圆弧,从z轴负方向看去,这段圆弧可以看作形成齿面的齿廓圆弧在S平面内的投影绕齿轮轴线旋转了Δψ角度后得到的。当然,齿廓上对应的两点与齿轮轴心连线的夹角也为Δψ,在图2中Δψ即为直线OA1与,OA2与,…OAn与之间的夹角。假设在齿轮端面上螺旋线z轴的坐标值为=pψ,11=p2ψ2,…=pnψn,则在S平面上螺旋线z轴的坐标值为=p1(ψ1+ Δψ)=p2(ψ2+Δψ),…=pn(ψn+Δψ)。又因为,-=-=…-=p1Δψ =p2Δψ =…pnΔψ=Δz(Δz为S平面与齿轮端面之间的距离),由此可知,p1=p2=…pn,也就是说这些螺旋线具有相同的螺旋参数P。因螺旋参数p=rcotβ,所以螺旋线所在圆柱面半径越大,其螺旋角也就越大。
要使一对圆弧齿轮能正确啮合,除了两齿轮的法面模数和压力角相等外,还须保证生成齿轮轮齿的齿轮节圆柱上的两条螺旋线螺旋角大小相等[1]。
2 圆弧齿轮的两条接触线间存在相对滑动的证明
根据式(2)可求得图3中两节圆柱上的圆柱螺旋线的长度。

式中:LP1—为齿轮1节圆柱面上螺旋线长度,LP2—为齿轮2节圆柱面上螺旋线长度。
由式(5)可得:

由式(2)求得接触线KA的长度LKA为:


图3 螺旋接触线所在的圆柱面半径的大小
图3O1K>O1P,并根据螺旋线性质知:半径越大,螺旋角也越大,所以:βKA>βP1。
由式(9),式(10)可得:LKB<LP2=LP1<LKA。
即两条接触线KA与KB的长度不等:

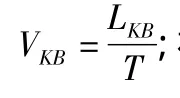

图4 圆弧齿轮接触线速度分析
在图4中,P为端面节点,K为接触点,KK'为啮合线,KA、KB为两圆弧齿轮的接触线。在某一瞬时,两齿面在K点接触,则接触点K相对于齿轮轴线O1O'1的速度为V1t,且V1t=O1K·ω1;接触点K相对于齿轮轴线O2O'2的速度为V2t,且V2t=O2K·ω2。将端面圆周速度V1t、V2t分别投影到相应螺旋线KA、KB的切线方向上,根据图2b几何关系,得:
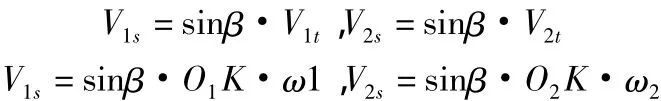
两齿面沿接触线方向的相对速度,即滑动速度ΔV=V1s-V2s=sinβ(O1K·ω1-O2K·ω2)。啮合点在接触线上的速度V1s是由沿啮合线KK'的速度Vz和圆周速度V1t合成,其中V1t=O1K·ω1;啮合点在接触线的速度V2s是由沿啮合线KK'的速度Vz和圆周速度V2t合成,其中V2t=O2K·ω2。因为在齿轮副啮合过程中,转动速度ω1和ω2是常量,所以圆周速度V1t和V2t是定值。沿节圆柱切线方向向下的速度Vz=p1ω1=p2ω2,式中p1=O1Pcotβp1,p2=O2Pcotβp2,所以Vz也是一定值。由平行四边形法则知,若两个分速度大小方向不变,则合速度就一定是方向恒定,大小不变的,即啮合点在接触线KA和KB上的速度V1s和V2s都是方向不变,大小恒定的。可得速度分别为:

可知速度V1s和V2s不相等。又因为在齿轮副啮合过程中,从某一瞬时开始,啮合点是从K点开始,同时沿接触线KA和KB的分别往接触线的另一端逐点依次移动的。那么,在移动过程中,啮合点在接触线上就存在速度差,那么,啮合点沿接触线方向上就一定存在滑动现象。滑动距离ΔL为:ΔL=LKA-LKB;滑动速度V滑为:

3 结语
圆弧齿轮副在传动过程中,啮合点在接触线上是滚动与滑动共存的一种运动现象。即齿面在接触线上啮合传动时存在滑动,而非经典著作中的纯滚动。由于接触线上各点的齿高不变,所以齿面磨损均匀,有利于磨合成理想的圆弧,跑合性好。
[1]邵家辉.圆弧齿轮[M].北京:机械工业出版社,1994.
[2]太原工学院齿轮研究室.圆弧齿轮[M].北京:机械工业出版社,1980.
[3]成大先,等.机械设计手册第五版[M].北京:化学化工出版社,2008.
[4]吴序堂.齿轮啮合原理[M].西安:西安交通大学出版社,2009.
[5]同济大学应用数学系.高等数学第五版[M].北京:高等教育出版社,2001.
——目镜套筒

