基于模糊Bow－tie模型的城镇燃气管道泄漏定量风险评价

於孝春 贾朋美 张 兴

1．南京工业大学机械与动力工程学院 2．中国石油管道科技研究中心

我国城镇燃气管道始建于20世纪七八十年代，受资金、技术等影响，管道的改建及维护困难重重，而且每年不断增加新管线，近几年达到敷设的高峰期［1］。燃气管道全生命周期的事故率服从“浴盆曲线”的规律，早期（半年以内）和末期事故频发［2］，目前我国燃气管道大部分处于早期或末期阶段；再者管线浅埋于人口密集的大街小巷，一旦出现事故后果影响十分严重。因此，迫切需要对燃气管道进行风险评价，将被动片面的事后响应变为主动全面的事前预防，以保障其长期安全可靠运行。

城市燃气管道的风险取决于管道失效的可能性和事故后果的严重性［3］，为将燃气管道事故的前因后果结合起来进行风险评价，首次引入Bow－tie模型，将风险分析中的故障树和事件树联系起来。Bow－tie模型最早出现在澳大利亚昆士兰大学关于帝国化学工业公司危害分析的课程讲义［4］，随后壳牌公司将其应用于阿尔法钻井平台爆炸灾难分析中［5］，至今这一技术已被广泛应用到一些重大事故。

燃气管道设计、运行、维护、巡线及周围环境等相关数据信息是风险评价的基础，由于历史原因，许多管道的资料缺失，给管理和评价带来困难。管道的风险影响因素很多，这些因素很难用精确值去表示。故本文将模糊集的相关理论引入燃气管道的风险评价中，其整体结构如下：首先借助模糊数确定燃气管道泄漏的可能值；再结合模糊层次分析法对泄漏后果进行权重分配，通过专家小组评价后果等级；最后借助案例进行分析，建立了燃气管道泄漏Bow－tie模型，最终得出评价结果，并给出相应的改进建议。

1 风险因素可能值的确定

1．1 模糊数表示的事件概率及运算

基于信息、模型以及人为因素的不确定性，事件发生的概率不宜使用精确值来表示，所以这里采用三角模糊数表示事件的概率值［6－7］，对事件的模糊性进行量化。三角模糊数可以用3个参数表示，记为A＝（a，m，b），其隶属度函数用公式表示为：

式中A是指定论域x上的模糊集；μA（x）是指x对模糊集A的隶属函数；m为模糊数A的均值；a、b分别为模糊数A的左右分布参数。

假设各事件相互独立，故障树中与门模糊算子为：

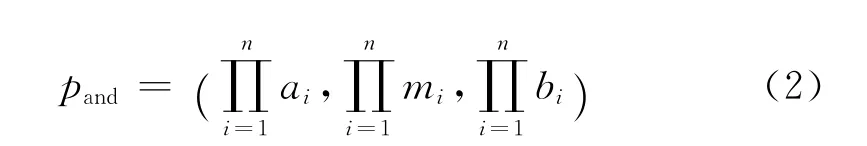
或门模糊算子为：

事件树中的模糊算子为：

式中i为某一基本事件；n为事件的个数；k为某一结果事件。

将引起燃气管道泄漏事件风险分为11个等级［8］，相应的语言变量及模糊数参照表1，语言变量可直观表达风险因素的相对重要性。

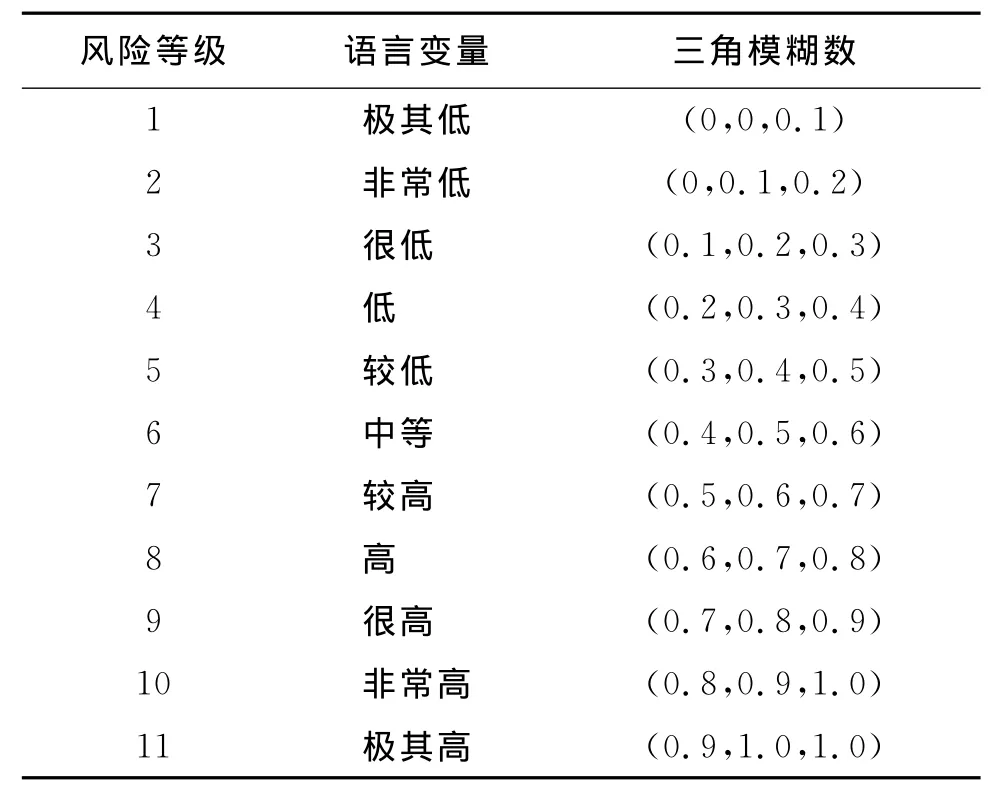
表1 以三角模糊数表示的事件风险等级表

1．2 模糊概率的聚合

在专家评分过程中，每个专家根据各自经验来判断不同事件的风险等级，所以对于不同专家的评价结果，还需进行模糊概率的合并以及专家权重的分配。对于模糊数的聚合，这里利用加权平均数法［9］：

式中Pi是聚合后的模糊数；Wj是第j个专家的权重因子；Pi，j是第j个专家为第i个基本事件分配的模糊数；n为基本事件数目；m为专家个数。

1．3 将模糊数概率化

由于求得的结果事件都以模糊数表示，为了对比风险的大小，需要将模糊数转化为相应的概率值，即FPS（Fuzzy Possibility Score）。在模糊集理论中，这个过程又叫解模糊化，这里是基于Chen和Hwang提出的模糊最大和最小集合方法［10］。该方法定义的最小及最大模糊集分别为：

则模糊数的左、右模糊可能值为：

则模糊数A的模糊概率值由以下公式求得：

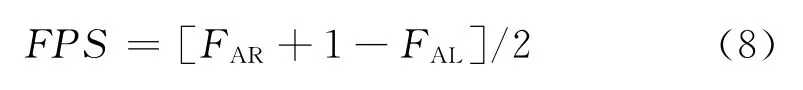
最后为了保证所有事件的真实概率和模糊概率之间的一致性，还需要将模糊可能值转化为模糊失效概率FFR（Fuzzy Failure Rate）［11］：

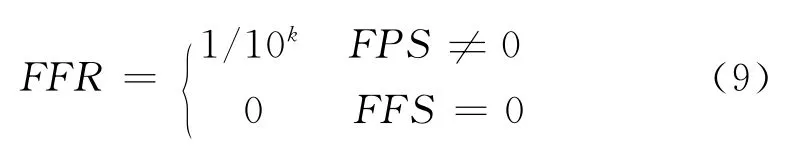
其中k＝ ［（1－FPS）／FPS］1／3×2．301。

2 燃气管道泄漏后果分析

当燃气管道发生泄漏后，会给人员、财产、环境及社会带来不同程度的影响。其后果就从人员、财产、环境及社会4方面来考虑，具体受影响因素参照图1。

图1 燃气管道泄漏后果图

2．1 确定各后果因素的权重系数

应用本文参考文献［12］中的模糊层次分析法，可得到第一级主因素，U＝｛A1、A2、A3、A4｝的优先关系矩阵：

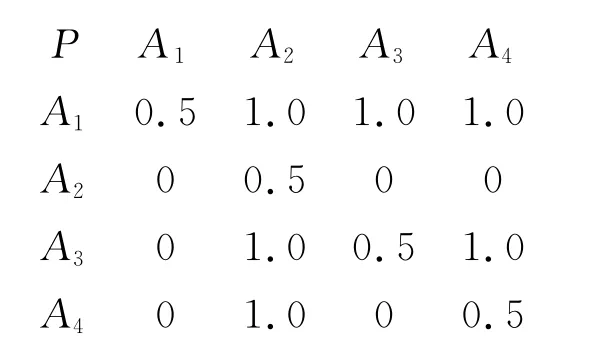
式中A1表示人员伤亡、A2表示财产损失、A3表示环境后果、A4表示社会后果。

应用本文参考文献［12］中的公式求得权重为（W人员伤亡，W财产损失，W环境后果，W社会后果）＝（0．4，0．1，0．3，0．2），同理求得第二级因素的权重（表2）。

表2 各后果因素权重表

2．2 确定燃气管道泄漏的后果等级

基于点火时机及空间大小限制，燃气管道泄漏表现出不同的形式，如爆炸、火球、蒸气云爆炸、闪火、气体堆积以及安全泄放等，不同形式造成的后果有轻有重，因此将后果等级也进行了分类（表3）。

3 燃气管道泄漏案例分析

如某市某段燃气管线穿越多条河流、公路、水塘，经过绿化带和农田，管道上方植被较多，街道沿线人口密集，车辆来往频繁，多条高压线横跨上方。通过对该段管线综合评估及开挖检测，得出腐蚀、第三方破坏、不合理设计及误操作是引起管道失效的主要原因。

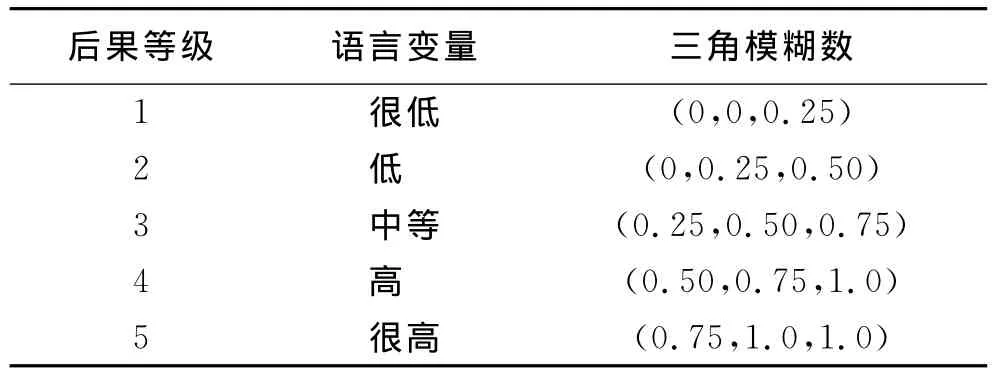
表3 以三角模糊数表示的后果等级表

3．1 建立Bow－tie模型

此燃气管段的Bow－tie模型中的顶事件为燃气管道泄漏，其故障树及事件树组成部分见图2，故障树中的基本事件见表4。

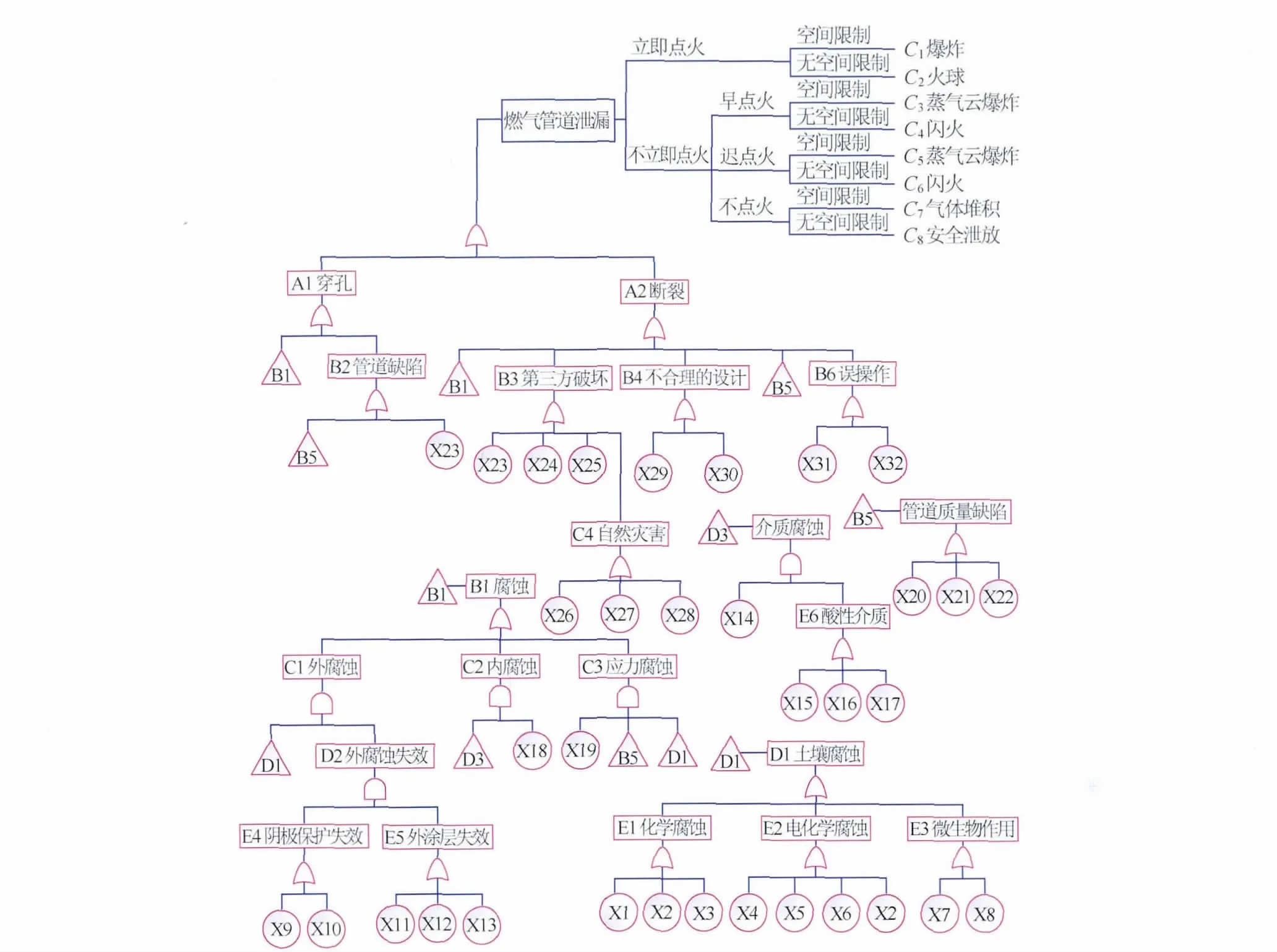
图2 燃气管道泄漏Bow－tie图

3．2 专家评价

首先邀请有经验的专家组成评价小组，再对专家进行权重分析，本文仅以两位专家为例，并且赋予其相等的权重。依据故障树中基本事件和事件树中诱发事件的风险大小，由专家赋予每个事件相应的三角模糊数，评价结果见表4，然后根据式（5）求得聚合后的事件模糊数。

3．3 Bow－tie模型中结果事件的发生概率

根据式（2）、（3）求得顶事件燃气管道泄漏的模糊数值L＝（0．57，0．89，0．99），再根据事件树模糊算子式（4）求得泄漏造成的C1（爆炸）、C2（火球）、C3（蒸气云爆炸）、C4（闪火）、C5（蒸气云爆炸）、C6（闪火）、C7（气体堆积）以及C8（安全泄放事件）的模糊数（以Li表示，i＝1，2，3……8）。

3．4 Bow－tie模型中结果事件相应影响后果的计算

专家小组成员可参照三角模糊数表示的后果等级表，将燃气管道泄漏造成的爆炸、火球、蒸气云爆炸、闪火、气体堆积以及安全泄放分别带给人员、财产、环境、社会的影响后果进行评价，评价结果见表5。

在计算结果事件后果影响时将后果因素的权重与其相应的评价模糊数按矩阵乘法进行合并［13］。如C1事件造成的第二级因素人员伤亡的后果计算如下。

相应的求得：C1财产损失＝［0．40 0．65 0．90］

C1环境后果＝［0．25 0．50 0．75］

C1社会后果＝［0．50 0．75 0．10］

所以爆炸造成的总后果：

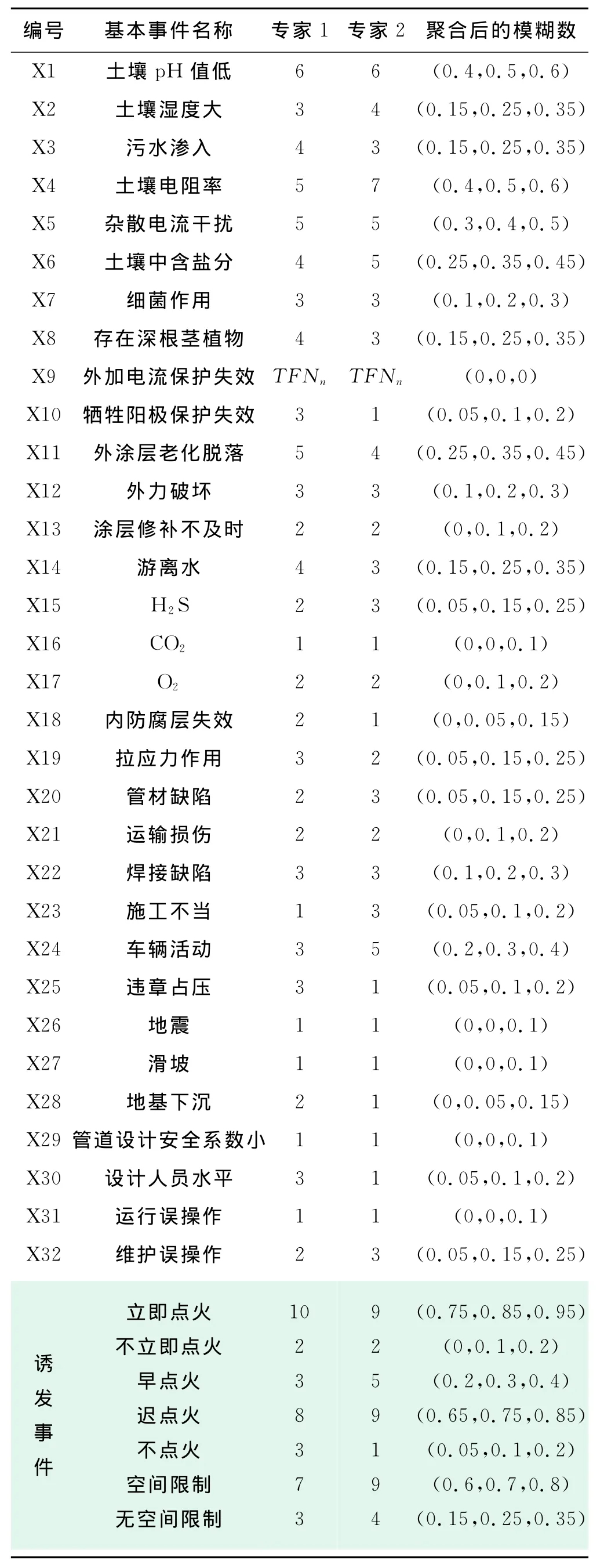
表4 各事件专家评价等级组表

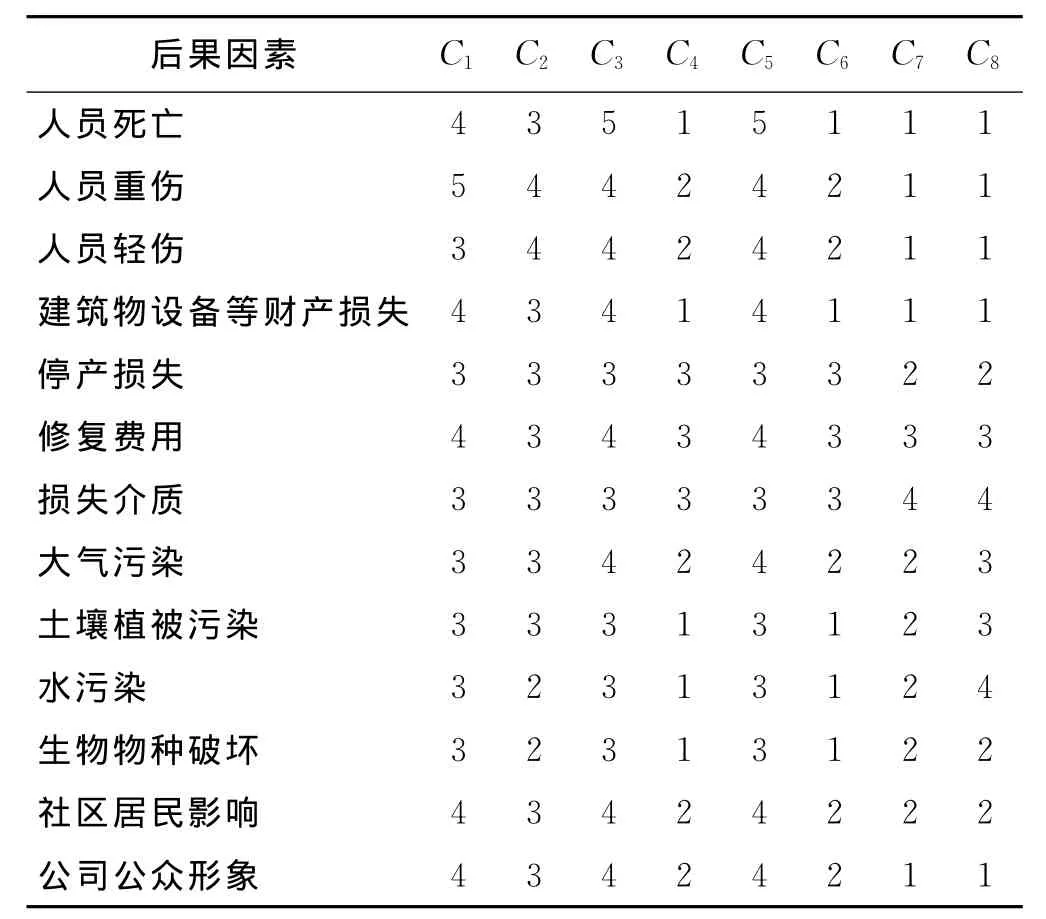
表5 结果事件的影响后果等级评价表

同理可求得其他泄漏事件造成的总后果值Ci。

3．5 风险评价

对燃气泄漏的风险评价可根据风险值Ri＝Li×Ci，由于计算的可能值和后果都以模糊数表示，所以为对比风险大小，应用式（6）～（9），将其转化为表6中的各结果事件的模糊失效概率值（FFR）。

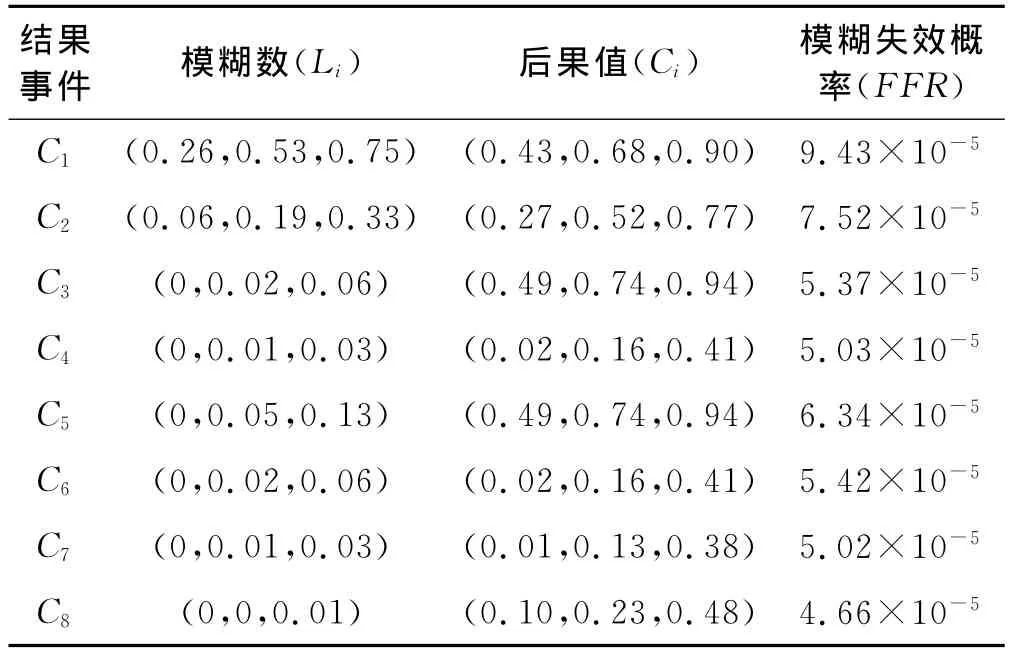
表6 结果事件的失效概率表

从各结果事件的模糊失效概率值可以看出，此管段一旦出现泄漏，发生爆炸的概率极高。因此需从引起泄漏的潜在因素中加以控制，从表4可以看出，土壤电阻率及杂散电流的干扰对管道影响较大，所以：①加强阴极保护措施，在牺牲阳极保护的基础上还要增加外加电流的保护；②及时维护外防护涂层；③加强巡逻、检测，重要管段可引入监控和数据采集系统SCADA，实时监控管道的运行状况，对于严重破坏的管道立即进行更换。相对来说安全泄放的概率低且后果影响也小，但会造成资源浪费，对环境影响较大，所以此次风险评价完成后，还需要进一步跟踪检测，在计划性维护后重新评价管道风险，建立以事前预控为主的燃气管道现代化管理方式。

4 结论

定量风险评价是燃气管道动态完整性管理的重要部分，本文基于模糊Bow－tie模型，将影响管道泄漏的风险因素及后果关联起来进行分析计算，根据评价结果可制订相应的检测计划，合理分配资源。

1）传统的概率分析需建立概率模型，但燃气管道经受各种不确定因素的影响，且各因素随机变化；由于人类知识的有限性难以确定精确的概率表达式，故本文借助三角模糊数表示事件的风险等级，通过模糊与门、或门计算，求得模糊可能值，然后解模糊化，对燃气管道的风险进行了评定，其结果更加符合客观实际。

2）利用模糊层次分析法确定了燃气管道泄漏各类次级因素的权重，使得泄漏后果的分析真实有效。

3）本次评价是以各风险因素相互独立为前提的，但工程实际中不仅要承认各因素的模糊性，还要考虑各因素间的关联，在这方面还需进一步探索。

［1］中华人民共和国住房和城乡建设部．全国城镇燃气发展“十二五”规划［EB／OL］．（2012－06－27）［2012－11－05］．http：∥www．mohurd．gov．cn／zcfg／jsbwj＿0／jsbwjcsjs／201207／t20120719＿210699．html．Housing and Urban－Rural Development of the People＇s Republic of China．The"Twelfth Five－Year"Plan of urban gas development［EB／OL］．（2012－06－27）［2012－11－05］．http：∥www．mohurd．gov．cn／zcfg／jsbwj＿0／jsbwjcsjs／201207／t20120719＿210699．html．

［2］汪涛，张鹏，刘刚．城市天然气管网运行的可靠性分析［J］．油气储运，2003，22（3）：15－18．WANG Tao，ZHANG Peng，LIU Gang．Analysis on the safety and reliability of city gas pipeline network［J］．Oil ＆Gas Storage and Transportation，2003，22（3）：15－18．

［3］陈伟珂，马法平．基于风险检测的埋地燃气管道失效可能性分析［J］．天然气工业，2009，29（8）：113－115．CHEN Weike，MA Faping．Failure possibility analysis of buried gas pipelines by the risk－based inspection（RBI）［J］．Natural Gas Industry，2009，29（8）：113－115．

［4］LEWIS S，SMITH K．Lessons learned from real world application of the Bow－tie method［C］∥American Institute of Chemical Engineers 2010Spring Meeting．Texas：AIChE，2010．

［5］PRIMROSE M J，BENTLEY P D，van der GRAAF G C，et al．The HSE management system in practice－implementation［C］∥SPE Health，Safety and Environment in Oil and Gas Exploration and Production Conference，9－12June 1996，New Orleans，Louisiana，USA．New York：1996．

［6］张艳丽．压力容器可靠性分析的模糊故障树方法［J］．机械设计与制造工程，2002，31（5）：30－34．ZHANG Yanli．The fuzzy fault tree method used in analysis of pressure vessel reliability［J］．Machine Design and Manufacturing Engineering，2002，31（5）：30－34．

［7］董玉革，朱文予，陈心昭．模糊故障树分析及应用［J］．合肥工业大学学报，1996，19（4）：35－41．DONG Yuge，ZHU Wenyu，CHEN Xinzhao．Fuzzy fault tree analysis and its application［J］．Journal of Hefei University of Technology，1996，19（4）：35－41．

［8］LEE H M．Applying fuzzy set theory to evaluate the rate of aggregative risk in software development［J］．Fuzzy Sets and Systems，1996，79：323－336．

［9］FERDOUS R，KHAN F，SADIQ R，et al．Handling and updating uncertain information in Bow－tie analysis［J］．Journal of Loss Prevention in the Process Industries，2012，25：8－19．

［10］CHEN S J，HWANG C L，HWANG F P．Fuzzy multiple attribute decision making：Methods and applications［M］．New York：Springer－Verlag 1992：138－150．

［11］ONISAWA T．An approach to human reliability in manmachine systems using error possibility［J］．Fuzzy Sets and System，1988，27（2）：87－103．

［12］张琳，李长俊，苏欣，等．模糊层次分析法确定管线风险因素权重［J］．石油机械，2006，34（6）：43－45．ZHANG Lin，LI Changjun，SU Xin，et al．Determination of pipeline risk factor weight by fuzzy analytical hierarchy process［J］．Petroleum Machinery，2006，34（6）：43－45．

［13］SHAHRIAR A，SADIQ R，TESFAMARIAM S．Risk analysis for oil ＆ gas pipelines：A sustainability assessment approach using fuzzy based Bow－tie analysis［J］．Journal of Loss Prevention in the Process Industries，2012，25：505－523．