基于应变设计管道局部屈曲应变极限值的计算

李 璞 陶燕丽 周 建

1．中国石油集团工程设计有限责任公司西南分公司 2．浙江大学滨海和城市岩土工程研究中心

传统的基于应力的管道设计方法保证外载产生的管道应力或等效应力不高于管材的允许应力（一般为最小屈服应力与折减系数的乘积），虽为管道的安全运营提供了一定的安全保障，但对于诸如地震、滑坡、海底管道敷设等位移控制载荷的管道，应变易超过允许应力所对应的应变值，该方法不再经济适用，应采用基于应变的设计方法［1－15］。基于应变的管道设计理念是建立在极限状态设计思想和位移控制载荷作用的基础上，对于位移控制的管段，在保证管道安全运营的前提下，允许管道的应力超过屈服应力。此时的管道虽发生一定塑性变形，但仍能满足运行要求，能充分发挥管道材料的性能，节约成本。

目前国内外管道的设计仍是以应力极限值作为评判标准，已有的各国管道设计规范也主要采用基于应力的设计准则，对管道基于应变的设计亦有提及，但涉及内容不一，如加拿大陆上管线（CSA Z662—2007，以下简称CSA）和挪威海底管线（DNV OS－F101—2007，以下简称DNV）提供了较为完整的管道基于应变的设计准则，两者都强调对管道进行应变设计时，应考虑管道可能的所有失效模式，并针对各失效模式采用不同的应变极限值，而美国海底管线（APIRP 1111—1999，以下简称API）和美国船舶部《海底管道建设指导》（ABS—2006，以下简称ABS）中仅包含管道同时受弯曲应变和外压作用时的抗屈曲应变设计准则。基于此，笔者对已有管道规范基于应变设计的内容进行了总结，以期对管道基于应变设计准则在国内外管道规范中的应用有个大致了解。

另外，长距离输油气管道的发展以及海底管道建设的日益增多对管道的性能提出了更高的要求，使得管道的刚度越来越柔、厚度越来越薄，成为典型的薄壳结构，这种薄壳结构会在内压和外力作用下发生局部屈曲失稳破坏。为此，对相关规范中局部屈曲失效模式下管道基于应变的设计进行了比较，其中CSA、DNV、API（与ABS相同）提供了管道在局部屈曲失效模式下的应变极限值计算公式，日本的SUZUKI等［11］也提出了较为简单的管道屈曲应变极限值计算公式，4类公式差异较大。基于一系列实际管道数据，采用上述4类公式对管道局部屈曲时的应变极限值进行计算，比较了4类公式的异同，并对管材应变硬化性能对管道屈曲应变极限值的影响因素进行了探讨。

1 基于应变的管道设计

1．1 基于应变、应力的管道设计准则

传统的管道设计采用基于应力的设计准则，它一般规定管材的应力不应超过其本身的屈服应力，即

式中σ为管材应力；σs为材料规定的最低屈服应力；k为设计系数。

基于应变的管道设计一般以管道的应变极限值作为失效判据，即

式中ε为管材应变；εcrit为某失效模式对应的极限应变；γ为设计系数。

CSA和DNV采用极限状态设计方法，两者均提出应根据管道可能的失效模式对其进行基于应变的设计，不同的失效模式应采用不同的应变极限值，如CSA提出了管道在主要荷载、次荷载以及主次荷载共同作用下时，为防止薄膜状破裂，其拉应变需满足下式：

式中εtf为纵向或环向拉应变（已乘分项系数）为管壁或焊接件的极限拉应变，即与薄膜状破裂失效模式对应的管道应变极限值；εt为拉应变的抗力系数。

1．2 主要相关规范

各国管道规范涉及基于应变的设计内容总结如表1所示。根据各国管道规范中涉及管道基于应变设计内容的多少，可将规范分为3类：①既包括以应力为基础的设计准则，又包括以应变为基础的设计准则，有挪威船级社《海底管道系统》（DNV－OS－F101—2007）和加拿大标准协会《油气管线系统》（CSA Z662—2007）；②允许以应变为基础的设计准则，但没有具体条款规定，有美国机械工程师学会《油气输配管道系统》（ASME B31．8）、美国石油协会《管线焊接和联结设施》（API 1104）和澳大利亚《石油和天然气管线 第一部分：设计和施工》（AS 2885－1—2009）；③包含了部分特定管道以应变为基础的设计准则，有美国石油协会《碳氢化合物海底管道设计、建设、运行和维修》（APIRP 1111—1999）、美国船舶部《海底管道建设指导》（ABS—2006）和美国生命线联盟《埋地钢管的设计指导》（ALA—2001）。

1．3 规范适用情况

对于基于应变管道设计方法的适用情况，DNV和CSA规范有较多说明，其他规范几乎没有提到。因此，以下仅介绍DNV和CSA规范中的内容。

DNV和CSA规范均指出基于应变的管道设计方法适用于受位移控制（或变形控制）的管道，同时也提到管道在载荷控制时应采用基于应力的设计准则。DNV对位移控制的定义为结构响应主要由几何位移控制，而载荷控制是由所施加的荷载控制。CSA采用变形控制这一名词，并指出在变形控制情况下，只有管道的变形能够引起结构的应变，而在载荷控制情况下，当外加荷载超过结构的承载能力时，管道的应变会大幅增加。由此可见，DNV和CSA中位移控制（变形控制）或载荷控制的概念基本一致。

表1 基于应变管道设计的规范总结表

DNV和CSA规范对管道基于应变设计方法的适用情况还作了进一步说明。CSA指出在下列情况下可采用基于应变的设计准则替代基于应力的设计准则：①非周期性位移控制情况下的管道变形，如永久性地面变形，或环境荷载引起的支撑移动，包括下沉、冻胀、融化沉降、地震断层运动和沙土液化；②非周期性载荷控制或位移控制情况下的管道变形，且管道的位移受固定几何约束的限制而不致超过许用应变极限值，这种情况适用于有限间隔距离的管道跨越；③管道初期受到非周期性最大荷载的作用，后续无塑性变形的产生，此时管道具有弹塑性变形。DNV规范在其条文说明中也给出了管道位移控制和载荷控制的实例，并指出无法严格判断某种工况是位移控制还是载荷控制，因为实际工程中两种控制可能会同时存在，这种情况下基于应力的管道设计准则和基于应变的管道设计准则均可应用，但后者更为经济合理。因此，设计时应充分利用管道位移控制的有利性。

综上所述，DNV和CSA规范均强调基于应变的设计方法适用于受位移载荷作用、可能发生较大变形的管道，如海洋管道、极地冻土区管道、地震引起沙土液化、滑坡等地段的管道、活动断层段管道和采空区段管道等。另外，对于延性高的管材，应用基于应变的管道设计准则也更为合理，因为该类管道在载荷作用下产生应变后，外载荷会被管道变形吸收而降低［12］。

2 局部屈曲

长距离输油气管道周围环境复杂，地理条件多变，不可避免地会遇到各种各样的地质问题，如深厚软土地区地基的不均匀沉降等，海底管道在敷设或运营过程中还需要克服外部高—超静水压力和内外高温差等不利条件，这些均对管道的性能提出了更高的要求，也促进了管道向大口径、高钢级、薄壁厚方向发展，并衍生为薄壁型空间结构。这种薄壁结构在内压和外力作用下易在管内局部产生较大变形，导致管道断裂或破坏，发生局部屈曲失稳［13］。因此，有必要对局部屈曲失效模式下的管道进行基于应变的设计。

局部屈曲失效模式以管道的压应变极限值作为控制标准。前面提到，对于局部屈曲失效模式下管道基于应变的设计，CSA、DNV、API提供了压应变极限值计算公式，日本的SUZUKI等也提出了管道的屈曲应变极限值计算公式［11］，其中，DNV、API适用于海底管道的设计，CSA对于陆上和海底管道设计均适用。

2．1 规范中局部屈曲压应变极限值的比较

2．1．1 DNV规范

DNV综合载荷、外压或内压等作用来确定不同载荷情况下局部屈曲的设计准则，它指出对于受纵向压应变（弯矩和轴力作用下）和内压的管道，局部屈曲设计时各截面应满足下列条件：

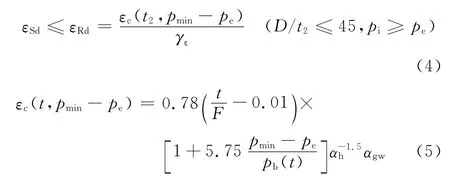
对于受纵向压应变（弯矩和轴力作用下）和外压的管道，设计时各截面应满足下列条件：

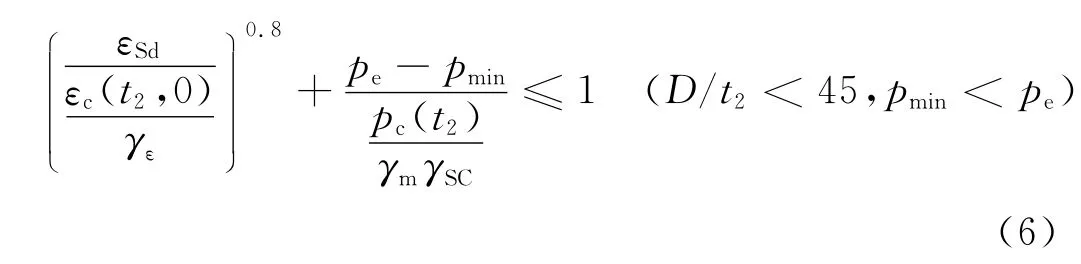
式中εSd为设计压应变，参见 DNV 中式（4．6）；pmin为在相关应变作用下管道的最小内压；pi为内压；pe为外压；pb（t）为允许压力，MPa；γε为应变抵抗系数，见DNV 中表（5．8），见DNV表（7．5）和表（7．11）；αgw为焊缝因子，见 DNV 中第 13 部分E1000条；D为管道外径，mm；t为管道壁厚，mm；t2＝t－tcorr，mm；tcorr为管道壁厚腐蚀裕量，mm；pc（t2）参见DNV中式（5．10）；γm为材料抗力系数，见DNV中表（5．4）；γSC为安全系数，见 DNV中表（5．5）。

2．1．2 CSA规范

CSA规定管道在荷载作用下，为防止局部屈曲，其纵向压应变应满足下式：

式中φec为压应变的阻力系数，见CSA中表C．3；εcrit为管壁的极限压应变能力；εcf为管道纵向或环向压应变（已乘以分项系数）。

CSA指出对于主荷载起主导作用的管道，纵向极限压应变取峰值荷载所对应的应变值。当缺乏详细资料时，可按下式（9）、（11）计算。对于次荷载（与内压联合作用）起主导作用的管道，当已考虑局部起皱、起皱区软化、截面失稳的影响时，管道可不受纵向极限压应变极限值的限制。这里的主荷载是指与管道变形无关、一旦施加就能在管内产生内力的荷载，如管道自重、管道内压等，次荷载是指管道受约束时才能引起内力的荷载，如温差荷载等。

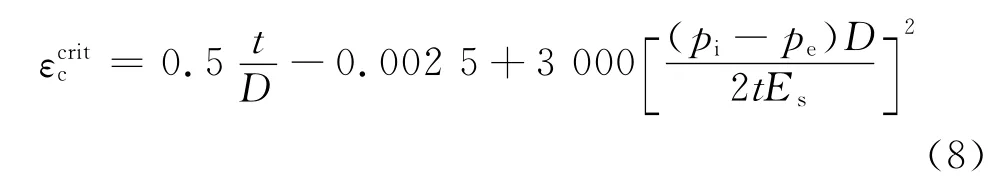
对于

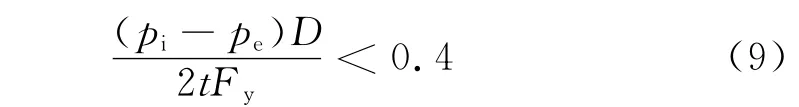
对于

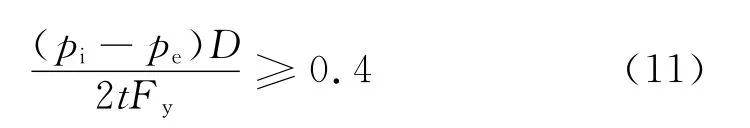
式中为管壁的极限压应变能力；pi为最大设计内压，MPa；pe为外部最小静水压力，MPa；Es＝207 000 MPa；Fy为有效指定的最小屈服强度（见CSA中C．5．7条），MPa。

2．1．3 API和ABS规范

API和ABS均指出管道在受弯曲应变和外压共同作用时其截面应满足下式：

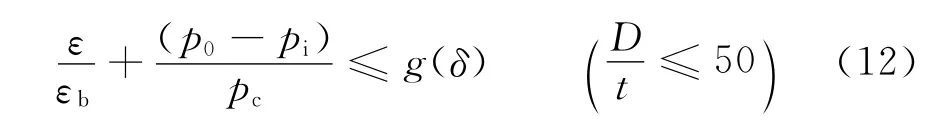
式中g（δ）＝（1＋20δ）－1，为破坏折减系数；δ为初始椭圆度取值不应小于0．5%；ε为管道的弯曲应变；εb＝t／2D，为纯弯曲时的屈曲应变；pe为管道的失稳压力；Dmax为任意截面最大直径，mm；Dmin为任意截面最小直径，mm。

2．1．4 日本SUZUKI公式

日本的SUZUKI等（以下简称JAP）用径厚比表示了管道屈曲时的最大压应变量［11］，即

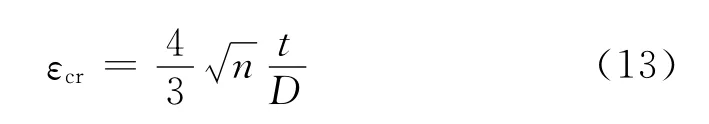
式中εcr为管道的压应变极限值；n为硬化系数，X65及以下钢级取0．11，X80HD1钢级取0．06，X80HD2钢级取0．09；t为管壁厚度，mm；D为管道外径，mm。

2．2 算例

某“西气东输”管道工程设计压力为10MPa，管道外径为1 016mm［14］，根据管道沿线地区等级的不同，采用了4组不同的管道壁厚（分别为14．6mm、17．5 mm、21．0mm、26．2mm）。参考此工程的设计参数，分别采用上述4类公式对不考虑设计压力和考虑设计压力两种情况下管道的压应变极限值进行了计算，设计参数见表2，计算结果如图1～5所示。需要说明的是，本文所采用的设计压力是指管道的内外压差值，且以下计算结果均是未考虑抗力系数或安全系数的管道压应变极限值。

表2 设计参数表

由于DNV和API中D／t的适用范围分别为D／t≤45（设计压力较低的陆上管线可认为其腐蚀裕量为0）和D／t≤50。因此图1～3中并没有对D／t超过限值的情况进行计算。

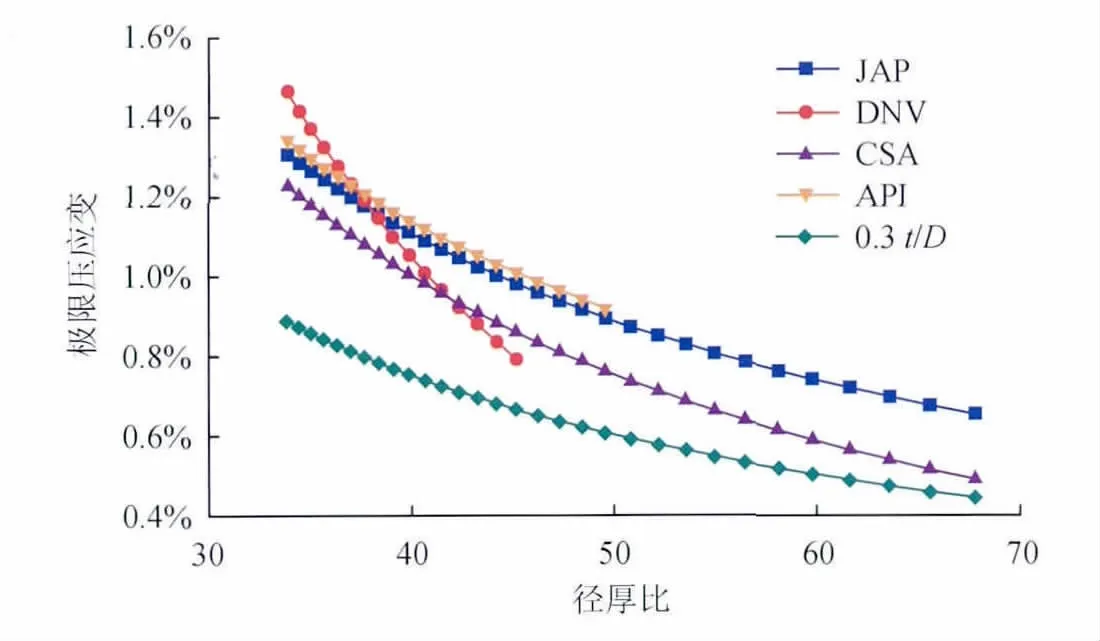
图1 不考虑设计压力时极限压应变随径厚比的变化图

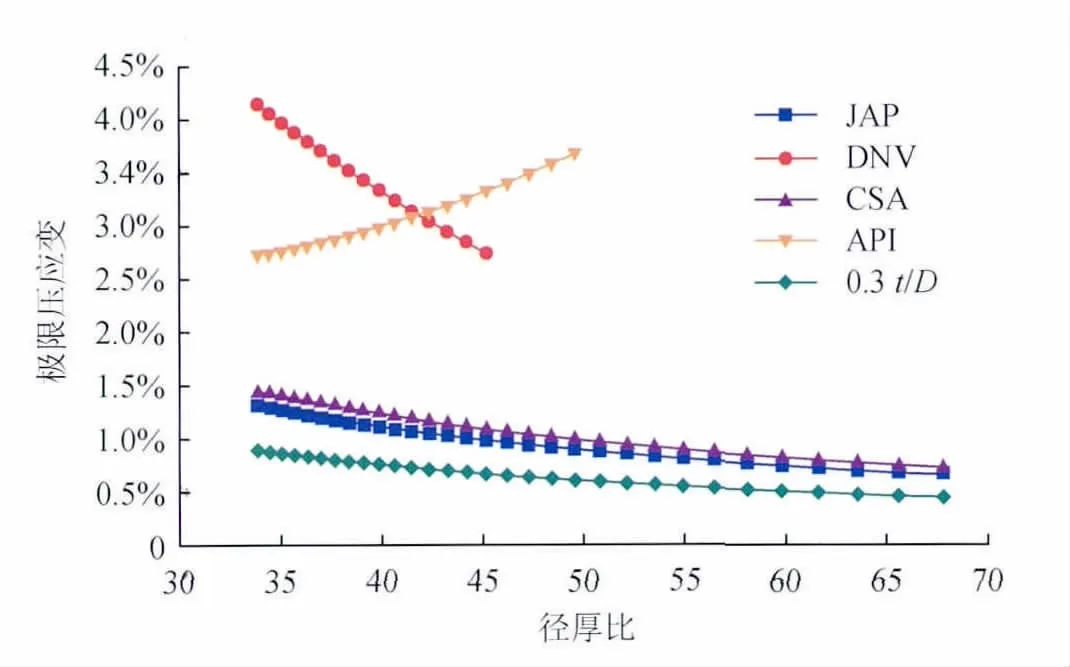
图2 10MPa时极限压应变随径厚比的变化图（X65钢）

图3 10MPa时极限压应变随径厚比的变化图（X80钢）

图1为不考虑设计压力时压应变极限值随径厚比的变化情况，可以看到，随着径厚比的增加，压应变极限值呈下降趋势。值得一提的是，在不考虑设计压力的情况下，DNV、CSA和API规范压应变极限值的公式仅与径厚比有关，而JAP公式由于考虑了管材的硬化，还与管线钢级有关。在考虑10MPa的设计压力情况下，如图2、3所示，对于X65和X80钢级，各曲线变化趋势基本一致：API规范压应变极限值随径厚比的变化趋势受设计压力影响，在设计压力较低时压应变极限值随径厚比的上升而下降，设计压力较高时呈现相反的变化趋势，这是因为API规范失稳压力与管道径厚比、管材泊松比、屈服强度、弹性模量有关，当管材级别确定时随着径厚比的增大而增大；CSA、DNV规范和JAP压应变极限值随着径厚比的增加而减小。当径厚比一定时，压应变极限值随设计压力的变化情况如图4、5所示。由图4、5可知，DNV、CSA和API规范压应变极限值随着设计压力的增大而增加，而JAP保持一个固定值。

图4 0～10MPa时极限压应变随设计压力的变化图（X65钢）

图5 0～10MPa时极限压应变随设计压力的变化图（X80钢）

整体来看，以上各图中JAP和CSA的曲线基本上都处于DNV和API曲线的下面，这说明JAP和CSA的计算公式更为保守。另外，为适应实际工程应用需求，建议用0．3t／D计算压应变极限值，以上各图中也给出了0．3t／D的曲线。与DNV规范等相比，可以看到，图1～5中，0．3t／D的曲线均在其他曲线的下方。因此，笔者认为文中建议的0．3t／D作为对压应变极限值的估计是偏安全的。由图4、5可知，X65和X80管线钢压应变极限值基本上随着设计压力的增大而增加，也就是说设计压力的存在有利于管道抵抗屈曲变形。同时由图4、5还可以看到，DNV和API曲线随着设计压力上升的幅度比CSA曲线大得过，CSA的计算公式更加安全，因此，对于压应变极限值的计算，当需要考虑设计压力的有利作用时，建议采用CSA规范中所提供的计算公式。

3 讨论

SUZUKI等通过试验和数值模拟等手段研究了材料性能对管道壳状屈曲强度的影响，结果表明管材的应变硬化系数的增加是导致管道非线性屈曲应变上升的关键因素之一，龚顺风等［16］通过数值模拟也得出大应变硬化系数材料制成的钢管失稳压力较大的结论。也就是说，应变硬化系数大的材料其抗变形能力强，对于应变硬化系数较大的管材，若不考虑应变硬化系数对其压应变极限值的影响，技术结果将偏于保守。

在上述4类公式中，SUZUKI等提出的JAP公式考虑了管材应变硬化系数对压应变极限值的影响，并建议对于X65及其以下钢级、X80HD1钢级和X80HD2钢级的应变硬化系数分别取0．11、0．06和0．09，但JAP公式仅仅与管材应变硬化系数和管道径厚比有关，未考虑设计压力或管材其他性能的影响；DNV、CSA和API规范考虑了管材的弹性模量、泊松比、屈曲强度以及设计压力等因素的影响，但均未考虑管材应变硬化系数的影响。目前还没有综合考虑管道设计压力、管材应变硬化系数以及其他材料性能影响的压应变极限值计算公式被提出，在这方面仍需更多的研究工作。

4 结论

已有的管道设计主要采用基于应力的设计准则，但对于位移控制情况下的管道，采用基于应变的设计方法将更为合理。对已有管道规范基于应变设计的内容进行了总结，并基于管道工程实例，在不同径厚比和设计压力下分别采用挪威、加拿大等规范中局部屈曲压应变极限值计算公式对管道压应变极限值进行了计算，结论如下：

1）CSA、JAP的压应变极限值计算公式比DNV和API的更为保守。

2）在不考虑设计压力的情况下，DNV、CSA和API压应变极限值的计算公式仅与径厚比有关，而JAP由于考虑了管材的硬化，其计算公式还与管线钢级有关。

3）API压应变极限值随径厚比的变化趋势受设计压力影响，而其他规范压应变极限值随着径厚比的增加而减小。

4）为了方便实际工程应用，建议取0．3t／D作为对管道压应变极限值的估计，对比研究说明，这样取值偏安全。

5）设计压力的存在有利于管道抵抗屈曲变形，当需要考虑设计压力时，压应变极限值的计算建议采用CSA中提供的公式。

6）已有规范中对管道基于应变设计内容的规定差异较大，我国管道设计标准的主要评判标准是应力准则，管道基于应变的设计准则还没有明确地提出和大范围地展开研究，本文的工作可为我国管道基于应变设计标准的建立提供参考。

［1］刘冰，刘学杰，张宏．以应变为基础的管道设计准则及其控制因素［J］．西南石油大学学报：自然科学版，2008，30（3）：143－147．LIU Bing，LIU Xuejie，ZHANG Hong．Pipeline design criteria based on strain and the control factors［J］．Journal of Southwest Petroleum University：Science ＆ Technology E－dition，2008，30（3）：143－147．

［2］VERITAS DET NORSKE．DNV OS－F101Offshore standard－submarine pipeline systems［S］．Norway：DNV，2007．

［3］Canadian Standards Association．CSA－Z662－2007Oil and gas pipeline systems［S］．Toronto：CSA Group，2007．

［4］American Petroleum Institute Publishing Services．API RP 1111Design，construction，operation and maintenance of offshore pipelines（limit state design）［S］．Washington DC：API Publishing Services，1999．

［5］American Society of Mechanical Engineers．ASME B31．8 Gas transmission and distribution piping systems［S］．New York：ASME，2003．

［6］American Petroleum Institute．API 1104Welding of pipelines and related facilities［S］．Washington DC：API Publishing Services，2005．

［7］American Bureau of Shipping．ABS 2006ABS guide for building and classing subsea pipeline systems［S］．Houston：ABS，2006．

［8］Australian Standard．AS 2885．1－2007Pipelines－Gas and liquid petroleum［S］．Sydney：Standards Australia，2007．

［9］American Lifelines Alliance．Guidelines for the design of buried steel pipe［S］．Sydney：Standards Australia，2001．

［10］中国石油管道建设项目经理部企业标准．Q／SY GJX 0136—2008西气东输二线管道工程强震区和活动断层区段埋地管道基于应变设计导则［S］．北京：石油工业出版社，2008．Company Standard for Pipeline Construction Administration Department．Q／SY GJX 0136－2008Guideline for the strain－based design in seismic area and active fault crossing of the West－to－East Pipeline Ⅱ Project［S］．Beijing：Petroleum Industry Press，2008．

［11］SUZUKI N，IGI S，MASAMURA K．Seismic integrity of high－strength pipelines［J］．JFE Technical Report，Oct．2008（17）：14－19．

［12］刘冰，刘学杰，张宏．基于应变的管道设计准则［J］．天然气工业，2008，28（2）：129－131．LIU Bing，LIU Xuejie，ZHANG Hong．Strain－based design criteria for pipelines［J］．Natural Gas Industry，2008，28（2）：129－131．

［13］金浏，李鸿晶．逆冲断层作用下埋地管道屈曲分析［J］．工程力学，2011，28（12）：98－104．JIN Liu，LI Hongjing．Buckling analysis of buried pipeline subject to reverse fault crossing［J］．Engineering Mechanics，2011，28（12）：98－104．

［14］宋苛苛．压力管道设计及工程实例［M］．北京：化学工业出版社，2007．SONG Keke．Design of pressure pipelines and the engineering projects［M］．Beijing：Chemical Industry Press，2007．

［15］AARON S D，RAYMOND J S．Strain based pipeline design criteria review［C］∥Proceedings of the 2ndIPC．New York：American Society of Mechanical Engineers，1998．

［16］龚顺风，陈源，金伟良，等．高静水压力作用下深海油气管道的局部屈曲［J］．浙江大学学报：工学版，2012，46（1）：14－19．GONG Shunfeng，CHEN Yuan，JIN Weiliang，et al．Local buckling of deepwater oil－gas pipeline under high hydrostatic pressure［J］．Journal of Zhejiang University：Engineering Science，2012，46（1）：14－19．