一种橡胶隔振器的设计方法

孟凡明，庞天照

(海军装备部驻沈阳地区军事代表局，辽宁沈阳110031)

0 引言

消除系统振动噪声的最好方法是减小振动源的振动，其中使用最广泛、最有效的方法是采用各种隔振器，以减小振动的传递［1］。由隔振原理可知，要获得良好的隔振效果，必须对隔振器的刚度进行设计。简单形状的减振器刚度特性可以通过经验公式进行计算［2］;形状复杂的隔振器，其刚度特性由形状系数决定，而且与减振器的使用状态有关。近年来，研究人员开始采用有限元的方法进行产品的设计［3-4］，不仅提高了设计精度，而且大大降低了设计成本和周期，给工程应用提供了巨大的便利。

本文采用经典算法对一种橡胶隔振器的静动态性能进行理论设计计算;在此基础上，利用Ansys有限元软件［5-6］，仿真分析隔振器的静动态特性，将理论计算结果和仿真计算结果与试验结果对比，验证设计方法的可行性，并为以后隔振器的设计提供帮助。

1 橡胶材料的特性

1.1 常规力学性能

在进行隔振器的结构设计时，必须了解隔振器中橡胶材料的常规力学性能，主要有应力应变关系、弹性模量、泊松比等，以便于设计计算。为此，对设计用材料进行单轴拉伸和单轴压缩试验，试验结果如图1和图2所示。

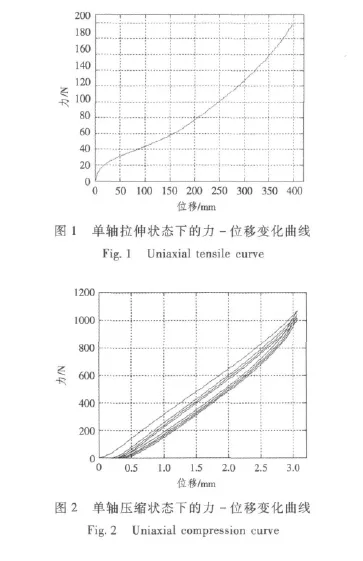
试验方法均按照国标的要求进行，并且通过多组试验选取性能稳定的结果作为设计参数。通过试验初步得到了材料的弹性模量为13.54 MPa。

1.2 动态力学性能

为计算橡胶材料在动态条件下的性能参数，对材料进行DMA性能试验，分别研究材料在压缩和剪切状态下动静比 (动态弹性模量与静态弹性模量之比)的变化，如图3和图4所示。

图3 压缩状态下的动静比变化曲线Fig.3 Static and dynamic stiffness ratio curve under compression state

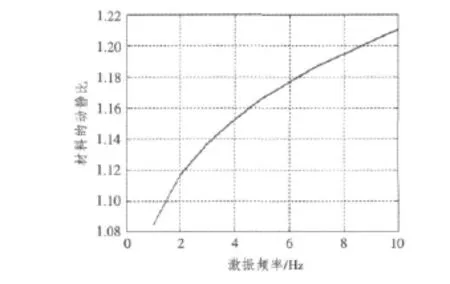
图4 剪切状态下的动静比变化曲线Fig.4 Static and dynamic stiffness ratio curve under shear state

从图3和图4可以看出，2种聚氨酯弹性体材料的动静比均随着激振频率的增大而增大，而且对于不同使用状态下 (压缩和剪切)，材料的动静比差别较大。因此，在考虑材料的动静比时需要综合考虑隔振器的受力状态和应力水平。

2 隔振器的理论设计

2.1 经典算法

初步设计一种剪切挤压型的橡胶减振器，其中橡胶部分可以简化为如图5所示单元，根据《橡胶工业手册》关于减振橡胶制品一节，可以得到图5所示单元的三向刚度为:

图5 隔振器中橡胶体简化单元示意图Fig.5 Schematic model of the structure of isolator

垂向刚度

横向刚度

纵向刚度

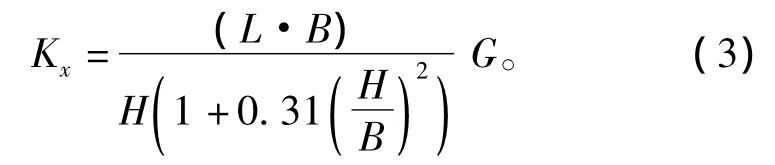
根据隔振系统固有频率的计算公式(4)，可以得到隔振器的动态条件下垂向固有频率

式中:M为减振器的额定载荷，kg;Kd为隔振器的动刚度，N/m;Ks为隔振器的静刚度，N/m;d为隔振器的动静刚度比，近似可以用橡胶材料的动静比来代替。

采用以上经典计算方法，初步计算得到的隔振器静态性能参数如表1所示。

表1 隔振器性能参数计算结果Tab.1 Calculate parameter of isolator

2.2 理论计算结果的修正

表1的计算结果是按隔振器初始状态为中心计算的，但是当隔振器承受了载荷之后，隔振器橡胶材料的倾角α和尺寸H都会发生变化，并由此引起隔振器性能参数的变化。为此，必须对隔振器的计算结果进行修正。在计算过程中，采用分布加载和迭代算法，直至加载至隔振器的额定载荷，计算结果如表2所示。

表2 修正后的隔振器性能参数计算结果Tab.2 Calculate parameter of isolator after modify

2.3 隔振器中橡胶材料应力校核和稳定性校核

2.3.1 应力校核

在进行隔振器设计时，必须校核隔振器中橡胶材料的应力，避免隔振器在使用过程中材料内部出现应力集中，导致材料出现疲劳破坏等现象。当隔振器垂向发生变形时，橡胶材料将发生压缩变形和剪切变形。

隔振器在额定载荷下变形量

求得弹性体压应力

剪应力

根据第四强度理论得到隔振器中材料内部应力为

弹性体发生塑性破坏的强度条件为

式中:［σ］为材料的许用应力。

隔振器中橡胶材料主要承受着压缩应力和剪应力，压缩应力约是剪应力的2～3倍，应力的大小和分布与隔振器的弹性模量关系不大，它仅取决于弹性体自身的尺寸和倾角。

采用式(8)分别计算了2种方案的隔振器在额定载荷下材料内部的正应力σ为0.86 MPa，剪应力τ为0.33 MPa，因此合成后的应力为1.04 MPa。该应力远小于橡胶材料允许的工作应力，满足设计要求。

2.3.2 隔振器的稳定性校核

为了检查隔振器在受到大载荷时材料会不会发生屈曲失稳，以致无法正常工作，采用欧拉公式计算材料的临界应力，对材料进行稳定性校核。

欧拉公式的普遍形式为

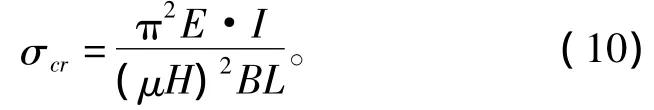
式中:μ为长度系数，它表示材料两端约束对临界压力影响，在设计结构中，μ取为0.7;I为截面两转动惯性矩中较小的1个。

采用欧拉公式得到隔振器的临界失稳应力为33.76 MPa，且临界失稳应力随材料弹性模量增大而增大。可以看出，隔振器中材料的临界失稳应力远大于工作时应力，因此，不会出现失稳现象。

3 隔振器的性能有限元仿真分析

3.1 橡胶材料的本构关系

橡胶材料的力学行为比较复杂，对环境条件、应变历程、加载速率等因素都非常敏感，其本构关系呈非线性，准确建立材料本构关系对于隔振器的有限元仿真至关重要。

根据单轴拉伸、压缩试验结果，采用名义应力和名义应变取值形式描述材料的应力-应变关系。结合隔振器的实际工作应变范围和已有的应变能函数对试验数据进行拟合，并对拟合结果进行误差分析，发现Mooney-Rivlin本构模型在综合曲线形状和拟合质量2方面综合性能最好。采用Mooney-Rivlin本构模型得到的材料常数为:C10=0.207 MPa，C01=1.207 MPa。

3.2 隔振器性能分析

3.2.1 静态性能分析

由于结构的对称性，在建立模型过程中，仅建立了1/2的结构，如图6所示。

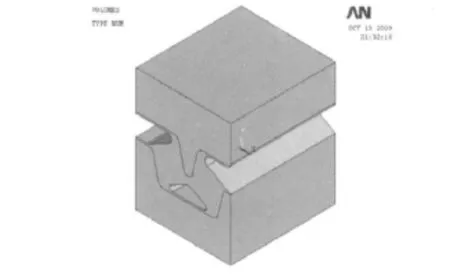
图6 隔振器有限元模型图Fig.6 Finite element model of isolator

通过垂向静态仿真计算，分别得到隔振器的性能参数，如表3所示。

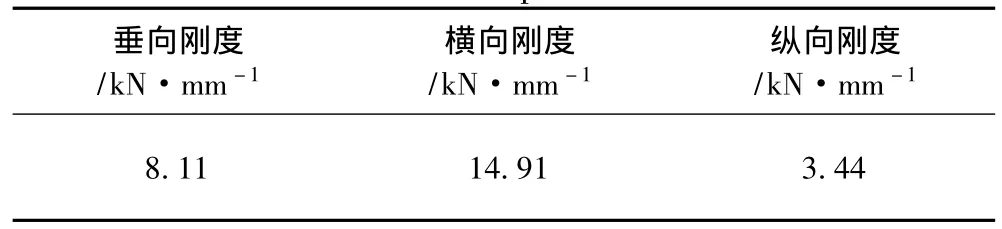
表3 隔振器静态性能参数仿真结果Tab.3 Imitate static parameter of isolator

3.2.2 动态性能分析

应用Ansys软件的模态分析模块对设计隔振器的动态垂向固有频率进行仿真计算。在模态分析过程中只有线性行为是有效的，将忽略所有的非线性因素，因此在分析过程中必须给定材料的弹性模量。因为隔振器是在动态条件下工作，所以必须给出材料的动模量。根据材料试验得到的动静比，可以得到材料的动模量，通过模态分析得到的隔振器在额定载荷下的垂向固有频率为9.23 Hz，垂向第一阶模态图如图7所示。

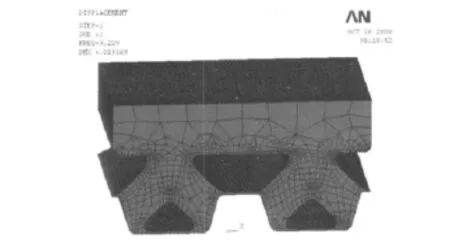
图7 隔振器垂向第一阶模态图Fig.7 First vertical mode for the isolator

3.3 对比分析

根据隔振器的试验结果，结合表1～表3对理论计算结果、仿真计算结果与试验结果进行误差分析，结果如表4所示。

表4 隔振器静态性能参数对比Tab.4 Static parameters contrast of isolator

从表4可以看出，隔振器在额定载荷下的纵向刚度采用2种方法计算的误差均在20%左右，而垂向刚度、横向刚度的误差均在10%以内，仿真结果优于理论计算结果。仿真计算得到的隔振器垂向固有频率误差大于理论计算结果，这是由于在仿真过程中材料的动静比取值不当引起的，需要对材料的动态性能进行准确的测量。

4 结语

本文对一种橡胶减振器的设计方法进行研究，采用理论计算和仿真分析2种方法分别计算了隔振器的静动态性能。通过与试验结果对比，得出以下结论:

1)在误差允许的范围内，理论计算和仿真分析结果与试验结果基本一致。

2)在进行隔振器结构设计时，可以采用理论计算和仿真相结合的方法，这样不仅可以大大缩短设计时间，而且可以节约设计成本。

［1］朱石坚，何琳.船舶机械振动控制［M］.北京:国防工业出版社，2006.

［2］林孔勇，金晟娟，梁星宇.橡胶工业手册(第六分册)［M］.北京:化学工业出版社，1998.

［3］陈莲.橡胶隔振器有限元分析与试验研究［D］.上海交通大学，2003.CHEN Lian.The rubber isolator finite element analysis and experimental study［D］.Shanghai Jiaotong University，2003.

［4］罗裕贤，易太连，欧阳光耀.橡胶隔振器动态特性仿真计算与试验研究［J］.机械与电子，2006(7):1114-1116.LUO Yu-xian，YI Tai-lian，OUYANG Guang-yao.Simulation and experimental study of the dynamic characteristics of rubber isolator［J］.Mechanical and Electronic，2006(7):1114-1116.

［5］张洪信，赵清海，等.ANSYS有限元分析完全自学手册［M］.北京:机械工业出版社，2008.

［6］张平，柴国钟，潘孝勇.橡胶隔振器静态特性计算方法研究［J］.振动测试与诊断，2010，30(2):105-110.ZHANG Ping，CAI Guo-Zhong，PAN Xiao-yong.The rubber isolator static characteristics calculation method［J］.Vibration Testing and Diagnosis，2010，30(2):105-110.