力学形心坐标计算对高等数学教学的启发

边平勇

(山东科技大学基础课部，山东 泰安 271019)

一个偶然的机会，发现《理论力学》期末考试答卷中全班同学在求解一个平面几何图形构件的形心坐标时，都采取套用教材中现成公式的办法来计算。教材中是如下计算形心的[1]:

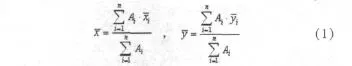
假设整个平面图形能够被分割成n块，其中Ai表示第i个小图形的面积和分别表示第i个小图形的横、纵形心坐标。基本上有两种方法可以用来计算，一是分割法，二是负面积法，这两种方法可以单独使用也可以结合起来使用。

试题要求计算如图平面图形的形心坐标:

学生忘记了高等数学重积分的应用中关于形心坐标的计算方法，事实上公式(1)也就是高数中形心坐标计算的特殊情况，有些教材也有由高等数学知识推导出公式(1)。但学生在解题时只会记已有的公式，全然忘记了可以利用重积分计算平面图形的重心坐标。高等数学重积分应用部分质心坐标计算公式为[2]

显然应用公式(1)和(2)分别计算上述构件形心坐标其结果是一样的。这是一个很简单的计算，原理是一样的，但发现整个班级没有一个学生应用重积分计算形心坐标。

我认为在高等数学的教学过程中要加强高等数学的专业教学意识。在大学一年级讲授高等数学重积分应用时，完全可以把这样的例子充实到课堂教学中，告诉学生这种例题是他们后续专业基础课力学知识学习中的一个具体例子，从而增加学生学习高等数学的积极性。同时告诉学生重积分还可以计算很多不规则平面图形以及空间立体图形的形心坐标。为了配合大学物理课的学习，在讲解微积分时可以补充向量积分计算方法。对于经管专业的学生可以引入有关边际成本、指数函数等有关的例题或知识点充实到高等数学的课堂教学中。这些做法有以下几个好处:

1.可以提高学生学习高等数学的积极性。通过这样的实例会使学生感觉到高等数学对于他们的后续专业课的学习具有非常重要的意义，从而重视高等数学的学习，提高将来后续课程的学习效果。

2.可以使高等数学的学习变得生动形象。通过高等数学专业教学意识的提高，可以让学生感觉的数学作为一种工具的强大，它能够解决生活中的实际问题，培养学生的建模能力，解决数学教学枯燥、无味的局面。

3.可以拓展学生的知识面。通过这样的教学可以使学生体会到数学与其它学科的交叉融合，尤其是工科课程。让学生感觉到数学类课程的基础地位，拓广学生的知识面。

4.培养学生应用数学知识的能力。加强数学实验教学[3]，以及专业实例的引用可以培养学生发现问题、分析问题、解决问题的能力，让学生提高数学素养，提高应用数学的能力，学以致用。

总之，我认为高等数学的教学不能拘泥于教材，应该具有高等数学专业教学意识。通过几轮这样的教学，积累一定的素材，可以编写适合不同专业的教材，因材施教，全面提高学生综合素质。

[1]《理论力学》[M].哈尔滨工业大学主编，北京：高等教育出版社，2002

[2]《高等数学》[M](第五版)上、下册，同济大学应用数学系主编，北京：高等教育出版社

[3]边平勇，吕端良，徐亚鹏.融数学实验的应用型本科《高等数学》教学探索[J].教育教学论坛，2012年S2期