基于MIND方法的钢铁企业能源系统建模与优化

陈 婧，戴毅茹，王 坚

(同济大学CIMS研究中心，上海 201804)

0 引言

钢铁企业作为一种典型的能源密集型企业，其节能措施包括两种途径:设备节能和生产过程节能。更新设备以换取能源消耗的降低，使得设备节能具有很高的成本门槛;而通过建立生产用能过程模型，优化生产过程中能源消耗，达到企业“节能减排”，这种生产过程节能方法可以被几乎所有企业采用。钢铁企业能源系统建模是进行能源系统优化的重要手段，然而现有能源系统建模对企业级能源系统建模的关注较少［1-2］。MARKAL(Market Allocation of Technologies Model)模型［3-5］、LEAP(Long-range Energy Alternatives Planning System)模型［6-7］等较成熟的能源系统模型，都属于区域系统模型，描述能源、经济和环境之间的关系。企业级能源系统模型，尤其针对钢铁企业的典型能源系统模型，却只停留在数学规划的建模方法上，没有完善的软件支撑。如文献［8］中根据宝钢生产系统和能源转换系统的特点，分工序按不同物流和不同种类能源分别建立了物流方程和能源方程，得到优化结果。但其所见模型缺少直观性和可视化性，无法形象描述企业的实际生产过程。

MIND 方法［9-10］(Method for analysis of INDustrial energy systems)是一种面向企业级能源系统建模及优化的重要方法，对于钢铁企业多设备、多过程以及串联、并联、反馈集一体的复杂生产过程，具有可视化建模、方便优化等特点。本文基于MIND方法，研究钢铁企业能源系统优化问题。

1 MIND方法

1.1 能源系统建模

基于MIND方法的企业能源系统建模，是指通过网络图建立企业能耗过程和产品生产过程。网络图由节点和连线组成［11］:节点描述的是能源和产品转换单元，连线描述能源和物料的转换以及传输路径，整个过程满足物料平衡和能量平衡。MIND建模示意图如图1所示，包括两种能源介质和两种物料，中间经过多个转换单元之后，生产出3种最终产品，图1中所有的节点和连线都包括若干方程，以描述物料和能源的消耗情况。

建模的过程包含两步，首先是对系统进行定界。定界要求不仅对整个企业有所了解，而且还要研究企业实际生产过程以及确定生产中的设备及其参数;其次是建立模型，连接各个设备，确定设备间的连线和能源流、物料流的流向，以模拟企业用能过程。

图1 MIND模型示意图

1.2 能源系统优化

通过能源系统建模，可获得一个优化目标函数和一组约束条件。优化的目的是，在满足约束条件之下，找到变量的值使得目标函数最小。但是，由于钢铁企业能源系统的复杂性，使得模型中的变量不仅包含连续性变量，还包含离散型变量(如二值变量)，这就使得钢铁企业能源系统优化问题不是一个简单的线性规划问题，而是一个MILP优化问题［12-14］。

MILP(Mixed Integer Linear Programming)混合整数线性规划法广泛应用于分析各种不同的系统。一个MILP问题包括，一个目标函数、若干变量和一些约束条件。MILP问题的描述如下:

目标函数:

约束条件:

在钢铁企业能源系统中，f(x，y)表示系统的总能耗;g(x，y)=0是一系列等式方程，描述系统的用能行为，如能源经过设备前、设备后以及在设备中消耗之间的关系;不等式方程组h(x，y)≤0，能够详细说明系统中的不等关系，如一台设备对能源或物料的存储容量;变量x是一组连续变量，代表所有的能源介质和物料;变量y是离散变量，又叫二值变量。

1.3 可视化工具软件ReMIND

在这里，笔者选择可视化工具软件ReMIND作为建模平台。可视化工具软件 ReMIND，是由瑞典Linkoping University基于MIND方法开发的软件系统。在ReMIND软件中建立钢铁企业能源系统模型，能够直观反映钢铁企业中多设备、多过程、串联、并联、反馈等能源消耗结构特点，并且此软件集建模与优化于一体，可有效输出优化结果。

ReMIND软件中所描述的能源系统模型，以标准化的形式表示，经过MPS产生器生成MPS文件，可将其保存，用于优化解算器优化。ReMIND软件中自带的优化解算器有CPLEX和Lp_solve。一般，还可以应用其它优化解算器进行优化(本文选用LINGO优化解算器)。ReMIND软件建模、优化流程，见图2。

图2 ReMIND建模、优化流程图

1.4 ReMIND中的函数方程

ReMIND软件中的函数方程，从各个方面描述每台耗能设备的工作状态，结合所建模型，能够准确模拟企业现实生产过程。在此，简单介绍一下ReMIND中的主要函数方程［15］，函数中出现的参数，命名如表1所示。

表1 参数命名

(1)目标函数。

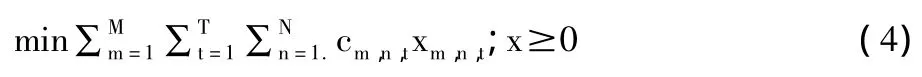
某时间步骤t，在第m个源节点的第n条流向上的流量是 xm，n，t，与之相对应的系数为 cm，n，t。所有时间步骤上所有源节点的流量和，是MILP问题中的目标函数，这里求其最小值。

(2)Source函数。

Source函数定义一种资源的源头，可以在Source函数中定义这种资源的单价。在节点上，针对某种资源设置了Source函数之后，就只有这种资源的流出流向，而没有流入流向。

(3)Destination函数。

Destination函数定义一种资源的最终存储处。与Source函数相反的是，针对某种资源设置了Destination函数之后，就只有这种资源的流入流向，而没有流出流向。

(4)Boundary函数。

Boundary函数是对一个节点的所有流入流量和设置的限制，它描述了一个加工设备的实际加工能力。

在任意时间步骤t上，对某个节点s的所有流入流量之和，应满足上述条件。

(5)FlowDependency函数。

FlowDependency函数定义两种资源的依赖关系，这两种资源可以是一同流入一个节点的不同资源，也可以是一种资源经过一个节点转换之后的另一种资源。

某任意时间步骤t，在s节点上的一种资源i与另一种资源j之间的依赖关系由cs，t确定。

(6)FlowRelation函数。

FlowRelation函数，定义同种资源在流入或流出一个节点时，不同流向间的比例关系。

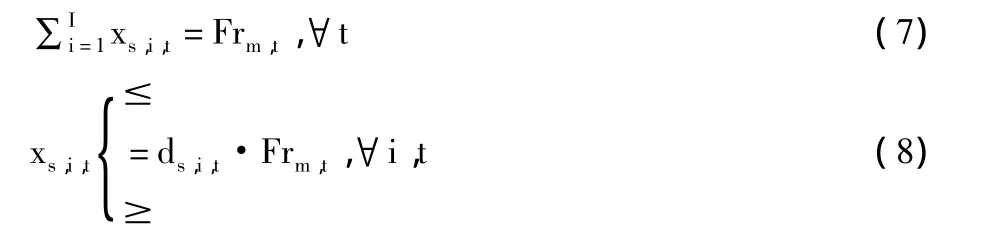
某任意时间步骤t，流入或流出节点s的流量和为 Frm，t，则不同流向的流量 xs，i，t有一定的限制大小如式(8)所示，ds，i，t是与之对应的介于0 与 1 之间的系数。

2 钢铁企业能源系统建模

2.1 钢铁企业能源系统特点

钢铁行业作为一个高能耗的行业，研究其生产过程中能源的使用情况，有很大的实际意义。但是，其特殊的企业生产过程，又决定了能源系统的复杂性:在生产过程中，物料和各种能源的持续消耗以及加工设备的连续运作，属于连续型生产过程;同时，诸如设备的开启和关闭等过程，又属于离散型生产过程。因此，钢铁企业能源系统是一个复杂的综合性生产能源系统。

某大型炼钢企业，是一个生产用能大户，该企业2010年主要产品产量135667吨，总综合能耗为231079.05吨标煤，其中锻件分厂生产锻件68312吨，能耗 114790.12吨标煤，占企业总能耗的近50%。本文针对企业中的锻件分厂进行建模，分析其能源使用情况，优化能源使用结构。

2.2 钢铁企业能源系统MIND模型

锻件厂中包括锻压过程和热处理过程，生产工艺见图3。钢锭成品高温加热后，经过水压机或者油压机进行压把、镦粗、强压、拔长和扩孔等;锻后进行热处理，消去应力，调整内部组织和增加机械性能。主要消耗能源为重油、煤气和电力，物料是钢锭成品。

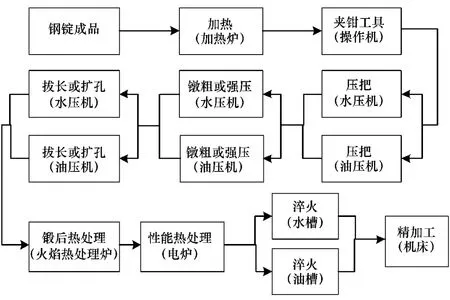
图3 某钢铁企业锻件生产工艺流程图

针对实际的锻件厂生产过程，本文首先对模型系统进行“定界”。在此，忽略能耗量小的以及降耗空间小的设备，如行车(吊运)、粗加工设备等，有效的设备有加热炉2台、操作机1台、水压机1台、油压机1台、热处理炉2台、电炉1台、重油回收设备以及水槽、油槽各一台。各种设备的加工能力和所需能耗如表2所示。根据一般企业应用的“单一制分时电价”制度，本文中将电力价格分为峰时段1.019元和谷时段0.488元。相应地，在模型中把Timesteps分2步，T1和T2。重油、煤气以及原材料钢锭，无论在T1时间段还是T2时间段，价格均相同，分别为2450元/tce、8554元/tce、5000元/t。设置各个设备的所需函数，建立能源系统模型见图4。

表2 设备信息表

图4 ReMIND软件中，某钢铁企业锻件生产能源系统模型图

3 钢铁企业能源系统优化

由于不同的时间步骤，其能源和物料成本不同，因此，本文先按照时间优化，使得目标函数最小，企业生产成本最低;在此基础上，再利用回收利用设备，对某些能源介质回收使用，研究其成本降低空间。

3.1 按时间优化

本文不考虑重油的回收利用，依据电力在不同时间段(T1、T2)的价格差异，对目标函数进行优化。

优化结果显示:目标函数1个(重油、煤气、电力以及钢锭的总价值最小)、变量77个、约束条件69个，若T1、T2两个时间段共生产200吨的锻件，则最低成本为811579.6元。其中，T1时间段生产50吨、T2时间段生产150吨;加热炉1处理钢锭80吨(T1:0，T2:80)、加热炉 2处理钢锭 120吨(T1:50，T2:70);水压机处理钢锭50吨(T1时间段工作)、油压机处理钢锭150吨(T2时间段工作);热处理时，选择耗煤气量较小的热处理炉2，耗煤气9.55tce;同理，选择水槽而非油槽进行淬火，耗电量0.62tce。

由于T1时间段为耗电峰时段，因此从结果中可以看出T1时间段生产的锻件明显少于T2，T2时间段生产满载。其他设备亦同时兼顾自身的生产能力及能耗量，当生产安排如以上所述时，能耗量最小，总成本达到最低811579.6元。

3.2 回收利用优化

加入重油的回收利用设备，对加热炉2的耗重油量进行回收利用，其工作耗电情况为X。

优化结果显示:重油回收利用设备回收1tce的重油所耗电量不同时，总成本不同，具体情况见表3。从表中可知，当忽略回收利用设备的耗电量时，系统总成本达到最低795470.9元，相对之前的811579.6元，总成本减少了16108.7元;当回收利用1tce的重油耗电量0.2958tce时，加或者不加回收利用设备的总成本相同(注:本文中所说的总成本不包含设备购置成本);耗电量大于0.2958tce时，回收利用使得总成本提升，直到耗电量为0.5tce，总成本变为恒量815622.1元。回收利用效果变化趋势图，见图5。

图5 回收利用效果变化趋势图

由于重油、电力分时段的成本不同，以及所加重油回收利用设备的耗电情况的不同，系统的总成本也不同。根据上述优化结果，在实际生产中，如果所加回收利用设备使得回收1tce的重油耗电量小于0.2958tce时，对整个生产系统的节能是有帮助的，此时可予以实施。如果相反，单从考虑总成本的角度来说，建议不要加回收利用设备。

表3 回收利用优化结果

4 结束语

MIND方法，作为一种专门面向企业级能源系统的建模及优化的方法，能够直观、可视化地描述企业的能源消耗过程。本文将其应用于某钢铁企业，了解其锻件生产过程中的能源使用情况，优化生产过程，能够为企业提供最优投入策略，使其总生产成本达到最小。

［1］Jebaraj S，Iniyan S.A review of energy models［J］.Renewable and Sustainable Energy Reviews，2006，10(4):281-311.

［2］Christos A Frangopoulos，Michael R von Spakovsky，Enrico Sciubba.A brief review of methods for the design and synthesis optimization of energy systems［J］.International Journal of Applied Thermodynamics，2002，5(4):151-160.

［3］余岳峰，胡建一，章树荣，等.上海能源系统 MARKAL模型与情景分析［J］.上海交通大学学报，2008，42(3):360-364，369.

［4］佟庆，白泉，刘滨，等.MARKAL模型在北京中远期能源发展研究中的应用［J］.中国能源，2004，26(6):36-40.

［5］Cosmi C，Cuomo V，Macchiato M，et al.Waste management modeling by MARKAL model:A case study for Basilicata region［J］.Environmental Modeling and Assessment，2000，5(1):19-27.

［6］遆曙光，王韵，徐广印.基于LEAP的居民生活能源与环境情景分析［J］.河南农业大学学报，2010，44(2):229-232.

［7］迟春洁，于渤，张驰.基于LEAP模型的中国未来能源发展前景研究［J］.技术经济与管理研究，2004(5):73-74.

［8］陈光，陆钟武，蔡九菊，等.宝钢能源优化模型的研究［J］.冶金能源，2003，22(1):5-9，37.

［9］Christer Ryman，Magnus Karlsson，Carl-Erik Grip.The MIND method for analysis of resource efficiency in industrial systems for materials production［C］//The 2nd International Seminar on Society＆ Materials.2008:1-10.

［10］Mei Gong.Optimization of industrial energy systems by incorporating feedback loops into the MIND method［J］.Energy，2003，28(15):1655-1669.

［11］Mehrdad Heidari Tari，Mats Soderstrom.Optimisation modeling of industrial energy systems using MIND introducing the effect of material storage［J］.European Journal of Operational Research，2002，142(2):419-433.

［12］Christodoulos A Floudas，Xiaoxia Lin.Mixed integer linear programming in process scheduling:Modeling，algorithms and applications［J］.Annals of Operations Research，2005，139(1):131-162.

［13］Haining Kong，Ershi Qi，Hui Li，et al.An MILP model for optimization of byproduct gases in the integrated iron and steel plant［J］.Applied Energy，2010，87(7):2156-2163.

［14］Patrik Thollander，Nawzad Mardan，Magnus Karlsson.Optimization as investment decision support in a Swedish medium-sized iron foundry-A move beyond traditional energy auditing［J］.Applied Energy，2009，86(4):433-440.

［15］Magnus Karlsson.The MIND method:A decision support for optimization of industrial energy systems-Principles and case studies［J］.Applied Energy，2011，88(3):577-589.