基于三维重建的绝缘子覆冰图像监测

杨 浩，吴 畏

（重庆大学 输配电装备及系统安全与新技术国家重点实验室，重庆 400044）

0 引言

我国是世界上输电线路覆冰最严重的国家之一，覆冰将使输电线路发生如倒杆（塔）、绝缘子串闪络等严重危害电力系统安全运行的事故，造成巨大的经济损失［1-2］。如2008年我国南方发生大面积冰雪灾害，导致高压线路杆（塔）倒塌17.2万基，低压线路倒塔断杆51.9万基，各级电压等级线路停运15.3万条，变电站停运884座，受灾损失严重［3］。因此，做好输变电设备覆冰的监测和预防工作对电力系统的安全运行具有重要意义。

目前国内外对输电线路和绝缘子覆冰的预测和监测进行了大量研究。文献［4］提出了采用旋转多圆柱体的覆冰厚度来估算绝缘子覆冰质量的预测公式，文献［5］通过微气象条件的实时观测结合模糊逻辑理论建立了线路的覆冰厚度预测模型。由于覆冰情况受到多个环境变量的影响，采用前述方法预测覆冰的厚度往往精度不高，工程应用中须采用更直接的监测手段。输电线路覆冰监测主要有绝缘子倾角［6］、导线拉力［7］、基于空气与冰的电阻和介电常数差异检测［8-9］、图像视频监测［10-12］等方式，其中前两者的覆冰厚度计算模型复杂，且覆冰导线的重力变化、绝缘子串倾斜角度和风偏角等参数为非同步采集，将导致较大计算误差；而由于冰和空气电传导性的复杂性及测量电路的干扰，基于电阻和介电常数差异的检测方法不易判别冰层厚度变点［13］，对于不规则覆冰形状的测量精度还有待进一步研究；采用图像视频监测的方法则能够直观地监测导线和绝缘子的覆冰状况。文献［11］通过对摄像机监测到的绝缘子覆冰图像进行图像边缘检测，提取出覆冰边界轮廓来测量覆冰的厚度；文献［12］利用图像滤波、自适应阈值变换和基于LoG算子的边缘检测技术对远程采集的覆冰图片进行处理和覆冰厚度识别。但现有图像监测方法都是对采集的二维图像进行处理和识别，受摄像机位置和角度影响较大，且通过二维平面对厚度进行估算在精度上很难达到实际要求。

本文提出一种基于计算机视觉技术的绝缘子覆冰图像监测方法，采用双目立体视觉技术模拟人的双眼观察事物，用2台摄像机从不同角度拍摄同一绝缘子覆冰情况，得到不同视角的覆冰图像，通过成像几何原理计算出覆冰绝缘子三维信息，从而构建出覆冰绝缘子的三维模型，再由三维重建模型计算绝缘子的覆冰厚度、体积等参数。该方法测量精度高，实现了远程智能监测，弥补了覆冰过程监测手段的不足，对于绝缘子覆冰的在线监测具有重要意义。

1 绝缘子覆冰图像三维重建原理

三维重建是指从单幅图像加景物约束或从2幅、2幅以上图像恢复空间点三维坐标的过程。本文采用基于双目立体视觉的三维重建，利用视差［14-15］的原理，即由2台摄像机从不同角度获取同一覆冰绝缘子的图像，这样绝缘子上的某一点在2幅图像中会呈现不同的视觉位置，再结合摄像机成像原理可计算出该点的三维坐标，然后构建物体的三维信息，近似于人类视觉系统的立体感知过程。

图1为简单的覆冰图像三维重建原理图，图像a和图像b是2台参数性能相同、位置固定的摄像机从不同角度拍摄到的绝缘子覆冰图像。图中，lb为摄像机投影中心的连线距离，lf为摄像机到图像平面的距离即摄像机焦距，摄像机光轴与图像平面的交点O1、O2为平面坐标原点。点P为空间中覆冰绝缘子上的一点，在左摄像机坐标系中的空间位置为（Xc，Yc，Zc），在 2 幅图像上的成像位置分别为 Pa（x1，y1）、Pb（x2，y2），通过相似三角形的几何关系可知：

图1 覆冰图像三维重建原理图Fig.1 Schematic diagram of 3D image reconstruction for ice-covered insulator

其中，x1、y1、x2、y2为平面图像中的已知坐标，lb和 lf分别为摄像机的外部和内部参数，为视差。图1所示的简单模型中y=y1=y2，因而视差为即点P在2幅图像中的位置偏移。可见由覆冰绝缘子上的一点在不同平面上成像的视差结合摄像机内外参数可计算出该点的空间坐标。而绝缘子覆冰的三维重建过程，就是在覆冰图像上找出大量能够表征绝缘子覆冰信息的特征点，计算这些点空间坐标的过程。当获得大量的覆冰绝缘子的特征点空间坐标后，将这些点组合起来就可构建三维模型，计算出覆冰的体积和厚度。整个三维重建过程主要分为4个部分：图像获取、摄像机标定、特征点提取和匹配、三维重建。

2 绝缘子覆冰图像三维重建方法

2.1 图像获取

通过安装在固定支架上的电荷耦合元件（CCD）摄像机采集现场图像数据，由于覆冰情况的测量要求范围不大且遮挡较少，两摄像机采用光轴平行、基线共线的位置布置，极大简化了后续处理过程。同时考虑到测量目标为覆冰的厚度，将摄像机上下平行布置，更容易得到垂直方向上的视差。用支架固定确保摄像机的相对位置不发生变化，摄像机相对位置发生变化则须重新对摄像机进行标定。图像获取示意图见图2。

图2 覆冰图像获取示意图Fig.2 Schematic diagram of insulator icing image capture

2.2 摄像机标定

由式（1）可知覆冰绝缘子上的点的空间坐标与摄像机的内外参数有关，为求得覆冰绝缘子上各点的空间坐标，就需要确定摄像机的位置、属性参数等，称为摄像机标定。其中摄像机的内部参数包括其图像中心、焦距、镜头畸变等，外部参数是指摄像机坐标相对于世界坐标系的三维位置和方向。

2.2.1 坐标系定义及转换

为了定量地描述摄像机成像过程，定义了世界坐标系、摄像机坐标系、图像物理坐标系、图像像素坐标系4个参考坐标系统［10］，如图3所示。世界坐标用来描述覆冰绝缘子的空间坐标，也是所要求取的坐标，其坐标原点可选在易于计算和观察的位置，如支架、杆塔或者绝缘子的顶端。摄像机模型采用针孔模型，简单实用并且准确，摄像机坐标系以摄像机光心为原点，沿光轴方向为z轴且垂直于像平面，z轴和像平面的交点O1为图像物理坐标系的原点。另外由于摄像机采集的图像以二维数组的形式储存，数组中的每一个元素即为像素，定义图像像素坐标系用像素坐标（u，v）表示该像素在图像上的列数和行数。

图3 坐标系示意图Fig.3 Schematic diagram of coordinates system

运用绝缘子上的点P在各个坐标系中的关系转换，计算其空间坐标。设覆冰绝缘子上一点P的世界坐标为（Xw，Yw，Zw），摄像机坐标为（Xc，Yc，Zc），图像平面物理坐标为（x，y），2个三维坐标系关系如下：

2个三维空间坐标系经过旋转和平移之后能够重合，因此 R 为 3×3 的正交旋转矩阵；T=［tXc，tYc，tZc］T为三维平移向量，（tXc，tYc，tZc）为世界坐标系原点在摄像机坐标系中的坐标；O为3×1的零矩阵。由图3中的三角形几何关系可以得到：

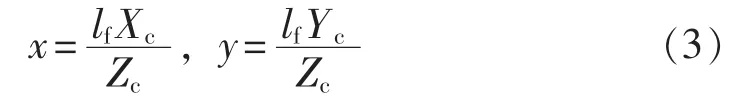
式（3）用齐次坐标可表示为：

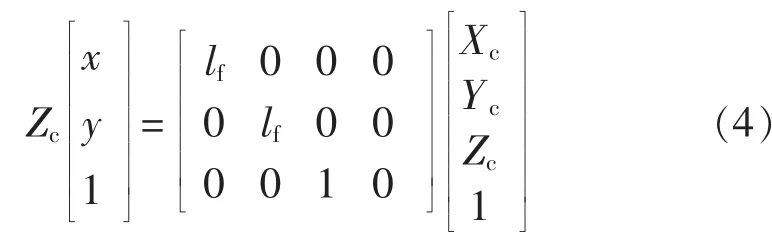
再将图像物理坐标转化为图像像素坐标。因为图像上的每一像素都有一定的长度，所以定义dx、dy分别为一单位像素在x轴和y轴上的物理长度，则点P的物理坐标和像素坐标之间的关系为：

其中，（u0，v0）是物理坐标系原点在像素坐标系中的坐标，（u，v）是点 P 的像素坐标。将式（5）代入式（2）—（4）可得：

其中，K1由摄像机内部参数决定，K2由摄像机相对于世界坐标系的方位决定，K1和K2即为需求解的摄像机内外参数矩阵。

2.2.2 棋盘格标定软件实现

摄像机标定的方法按是否需要标准的标定物分为三大类：传统标定方法、自标定方法和基于主动视觉的标定方法。传统标定方法需放置标定物，受环境制约；自标定方法精度较差；基于主动视觉的标定方法需精密仪器，价格昂贵。因此本文选择介于自标定方法与传统标定方法之间的张氏标定算法［16］。

张氏标定算法精度较高且具有较好的鲁棒性，其原理是借助一个具有精确定位点阵的标定模板（见图4），已知其世界坐标与1个以上不同方位的图像进行匹配，利用矩阵K1和K2计算出内外参数。同时由于透镜的结构特点，透镜在成像过程中会产生畸变且主要为径向畸变，如图3中P（x，y）为理想成像点，P（xq，yq）为实际成像点，需对平面坐标进行校正。张氏标定法中的畸变模型为：

其中，xq、yq、uq、vq为校正前的坐标；x、y、u、v 为校正后的坐标；采用最小二乘法，通过标定板图像上点的坐标求解方程组可得畸变系数k1和k2。

图4 试验采用标定模板Fig.4 Calibration target framework for test

张氏标定算法要求标定后摄像机坐标与世界坐标位置关系不发生变化，拍摄绝缘子时摄像机由支架固定且与绝缘子有固定的位置关系。选取单个绝缘子盘圆心为世界坐标系原点，钢帽和正对摄像机的方向分别为y轴和z轴，所用2台CCD摄像机上下距离30 mm，2号摄像机同绝缘子轴线相距300 mm。对2台摄像机分别进行标定，标定板大小为每格20 mm，格数14×9，将标定板贴于玻璃板中央处于坐标原点位置，与摄像机相距300 mm，变换标定板角度拍摄10张标定图像，图像分辨率1280×720，图片物理尺寸127 mm×89 mm。编程环境采用VC++，其OpenCV库提供了实现张氏标定算法的函数［17］，流程如图 5 所示。

图5 标定流程图Fig.5 Flowchart of calibration

通过以上程序对2台摄像机进行标定，2号摄像机的标定结果如式（9）—（12）所示。

其中，R′为旋转向量，是简化的旋转矩阵，可以利用cvRodrigues2（）函数进行转换。由内参数矩阵可知2号摄像机的有效焦距和基准点像素坐标。

最后还需进行误差分析，其做法是代入得到的内外参数矩阵，选取标定板外围4个角点计算最大尺寸与实际尺寸进行比较，最终得到在3个方向上的偏移均小于0.1 mm，在此不再进行详细叙述。至此，完成摄像机标定，下面将对绝缘子覆冰图像进行处理。

2.3 特征点提取和匹配

采用CCD摄像机采集到2幅绝缘子覆冰图像如图6、7所示，分别为1、2号摄像机所拍摄到的同一片绝缘子覆冰图像。摄像机标定工作完成后，再对目标图像进行处理、提取和匹配特征点从而计算三维坐标。摄像机拍摄到的绝缘子覆冰的二维图像，包含各种随机噪声和畸变，需对原始图像进行滤波去噪，突出绝缘子覆冰情况，改善图像质量。由于本文采用基于灰度变化的改进Harris算子提取特征点，因此先由中值滤波进行图像去噪，其原理是让与周围像素灰度值的差较大的像素改取与周围像素值接近的值，消除孤立的噪声，从而提高特征点提取的精度。

图6 1号摄像机拍摄的单片绝缘子覆冰图Fig.6 Image of ice-covered insulator captured by camera 1

图7 2号相机拍摄单片绝缘子覆冰图Fig.7 Image of ice-covered insulator captured by camera 2

特征点提取主要分为基于图像边缘的方法和基于图像灰度的方法。对于覆冰绝缘子不仅需要边缘信息，还需要整个绝缘子上的覆冰特征点，所以本文采用基于图像灰度方法的改进Harris角点检测算法。经典Harris算法［18］的思想是在图像中设计一个局部检测窗口，该窗口沿各方向微小移动，若窗口的平均能量超过设定的阈值就将窗口中心像素点提取为角点。Harris算法定义像素（x，y）自相关矩阵如下：

其中，Ix=∂f/∂x为像素点在x方向上的灰度变化，Iy=∂f/∂y 为像素点在 y 方向上的灰度变化；G（x，y，σ）为高斯函数。作为检测窗口其角点响应函数为：

其中，k为常数，一般取0.04～0.06；R在角点区域是正值，在边区域是负值，而在不变化的区域取值很小。将计算出的检测窗口中心点的R值与给定阈值比较，如果大于阈值该中心点即为角点。

Harris角点检测稳定性好且编程实现简单，但由于环境影响，覆冰图像上很多地方像素变化较小，用传统的Harris检测得不到所需的角点信息，因此采用改进的Harris算法。在Harris算法中以高斯函数作为检测窗口函数（即尺度），高斯函数不同则尺度不同，检测特征点会有所差别；而以单一尺度检测角点，在像素变化不大时容易漏检。在改进算法中先用大尺度进行粗略定位，再用小尺度进行精确定位从而准确提取角点。改进算法的像素点自相关矩阵为：

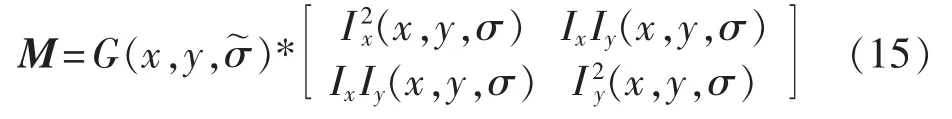
其中，Ix（x，y，σ）=Ix*G（x，y，σ），Iy（x，y，σ）=Iy*G（x，y，σ），IxIy（x，y，σ）=IxIy*G（x，y，σ）；=ασ，α 为不大于1的常数；角点响应函数不变。此外，由于环境等条件的不同会对图像的对比度造成影响，为此采用最大类间方差法确定最优阈值。将图像中的像素根据灰度值t分成两部分，0～t之间的像素组成C0，t～T（256级灰度图T=255）之间的像素组成C1。通过计算C0和C1的类间方差σ2（t）来确定阈值：

其中，P0（t）和 P1（t）分别为 C0和 C1的像素数，H0（t）和H1（t）分别为C0和C1中像素的平均灰度值。所取阈值即为0～T之间使σ2（t）最大的t值。通过检测试验表明，改进的多尺度Harris角点检测方法能够实现大尺度下的去伪角点和小尺度下对特征点的精确定位，错误率较低且精度明显提高。

在提取特征点后须找到匹配的像素点来计算出其三维坐标，针对覆冰的三维重建精度要求较高，匹配的特征点越多则精度越高，重建模型也越真实。在保证匹配精度的前提下减少计算量，采用改进的基于灰度相关系数图像匹配算法［19］以提高匹配速度。通过灰度相关系数表征灰度相似度，即计算相应区域的灰度绝对差，得到多个相关系数值，系数值越大，匹配程度越高。本文对1号摄像机图片中的每个特征点，在2号摄像机图片中对应区域以指定大小窗口搜索，计算相关系数，系数最大值对应的窗口中心就是最佳匹配点。对于2号摄像机图片特征点以同样方法计算1号摄像机图片中特征点的相关系数。由于窗口内所有特征点的相关系数计算量太大，需利用简化相关系数和设定阈值逐步缩小搜索范围，在减小计算量的同时达到实时高精度匹配要求。改进前后的相关系数公式和设定阈值逼近的详细过程可见文献［19］，匹配算法的软件编程仍采用VC++实现，根据图6和图7所计算得到特征点匹配结果如图8所示。

图8中显示了2幅覆冰图像的一部分匹配像素坐标及2号摄像机图片的部分角点检测坐标，其中1号摄像机图片检测角点1221个，2号摄像机图片检测角点1209个，最后建立匹配角点913对。由于绝缘子距离摄像机较近匹配程度高，而背景距离摄像机远、场景变化较大，所以匹配度低，因而特征点匹配时去除了300对背景特征点，最后保留的匹配点大部分为覆冰绝缘子上的点，但仍有一些无用的匹配点，可在三维坐标重建后通过与绝缘子径向距离比较来剔除。

图8 特征点匹配结果Fig.8 Results of feature point matching

2.4 覆冰绝缘子三维重建

得到了匹配的特征点像素坐标，且在2.2节摄像机标定中求出了摄像机内部参数、旋转矩阵和平移矩阵，根据式（6）可由匹配像素点坐标经矩阵计算得到匹配点的三维坐标，将这些点的深度坐标与绝缘子径向距离（280 mm）比较，去除属于背景的匹配点以及病态匹配点。然后在VC++中运用OpenGL编程导入三维坐标参数，实现覆冰绝缘子三维的点云显示［20］，并利用OpenGL提供的函数实现旋转、放大、缩小等功能得到图9所示的4个不同角度的绝缘子点云模型。

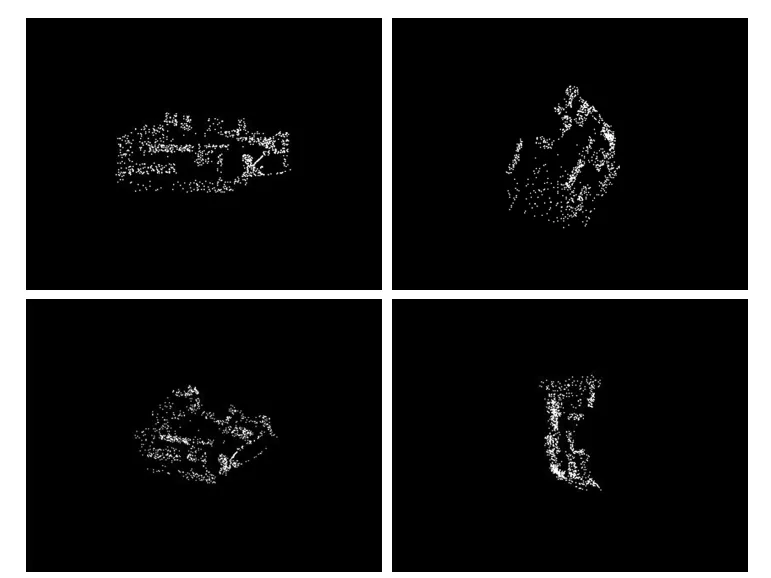
图9 绝缘子覆冰模型多角度视图Fig.9 Views of ice-covered insulator model from different angles

由旋转的绝缘子覆冰重建模型可清晰地看出绝缘子的覆冰形态和粗略地观察其覆冰的状况。采用MATLAB对点云模型的z轴数据进行三次插值拟合出其覆冰模型，如图10所示。

图10 绝缘子覆冰三维拟合模型Fig.10 Fitted 3D model of ice-covered insulator

由图10可见，仍然存在少数畸点，去除差异较大的点，采用数值积分算法，将每个点视作以z=0平面为底的极小立方体，对该覆冰模型上冰所包络的体积进行计算得到其总体积为V1，未覆冰时计及绝缘子槽的绝缘子体积为V0，即可得到该绝缘子上冰的体积为：

则覆冰重量为：

其中，ρ为冰的密度，图6、7中覆冰类型为雾凇，计算时 ρ取 0.5 g /cm3。

3 试验结果与分析

在第2节中通过覆冰图像对绝缘子覆冰模型进行了三维重建，并得到部分覆冰点云等数据。按照同样的方法，将摄像机绕绝缘子轴线水平旋转180°再次进行双目视觉的测量与重建，最终可得到完整的绝缘子覆冰点云模型，计算出整片绝缘子覆冰的体积。本文用三维重建的方法对图11中3片绝缘子进行了覆冰监测，绝缘子A、B、C最大覆冰厚度的位置分别为（-184.95787，45.52714，28.38611）、（-180.80687，0.566 20，-16.155 49）、（-187.512 39，39.779 46，-19.80815），试验所得其他数据如表1所示。由试验数据可知，通过三维重建测得：绝缘子A覆冰重量715.47 g，精度92.50%；绝缘子B覆冰重量877.49 g，精度91.97%；绝缘子 C覆冰重量523.39 g，精度92.49%。可见基于三维重建的覆冰监测能够达到较高的精度。

为保证实时的高精度监测，本文对三维重建算法进行了简化，若监测主机的硬件资源足够，可以改进特征点检测匹配算法以提高计算精度。由重建模型三维坐标还可以计算出覆冰的最大厚度，试验所得最大厚度及其所在位置为分析绝缘子的覆冰状况提供有利的依据，还能进一步估算绝缘子覆冰厚度分布情况，对掌握绝缘子状态、防止电力事故具有极大的价值。

图11 3组绝缘子覆冰试验Fig.11 3 groups of insulator icing test

表1 3组覆冰试验三维重建结果Tab.1 Results of 3D reconstruction for 3 groups of insulator icing test

4 结论

针对现有覆冰在线监测手段的不足，提出了基于三维重建的绝缘子覆冰图像监测法。应用双目视觉原理，通过覆冰绝缘子在2幅图片上的视差计算出绝缘子特征点的三维坐标建立三维模型。试验结果表明，三维重建模型可得到清晰的覆冰三维轮廓，还原度高，且便于把握绝缘子覆冰情况。除了得到覆冰的重量外，三维重建还能准确反映覆冰厚度分布状况，这对防止绝缘子闪络具有重大的意义。该方法在覆冰在线监测中引入了计算机视觉技术，但是不够完善，针对其不足之处可以做出如下改进：

a.摄像机标定需要摄像机和绝缘子相对位置不变，可以加入云台旋转计算旋转角度与平移矩阵、旋转矩阵的关系，避免摄像机位置变化后要重新标定；

b.采用像素更高的摄像机采集高分辨率的图片，可以提高角点检测和匹配的精度；

c.可对点云模型进行三角剖分再粘贴纹理，建立更为直观的立体模型，计算体积更为精确。