基于统计理论的含风电互联电网CPS研究

翁毅选 ，邓长虹 ，黄文涛 ，肖 水 ，颜 霞 ，赵维兴

（1.武汉大学 电气工程学院，湖北 武汉 430072；2.贵州电网公司，贵州 贵阳 550002）

0 引言

针对互联电网正常运行情况的频率控制性能，美国电力可靠性委员会（NERC）提出了基于严密统计学原理的 CPS（Control Performance Standard）考核标准［1］，但其主要是对含常规可控电源的互联电网频率控制性能进行评价，并没有考虑风电等不可控电源的影响。随着风电并网容量的持续增加，其固有的随机性和不确定性会导致系统有功频率的波动，这将给系统的频率控制带来极大的挑战［2-4］。而CPS作为衡量互联电网频率控制性能的关键指标，将会直接反映出风电接入以后对系统频率控制性能的影响，对风电并网以后的CPS的研究具有理论价值和实际意义。

当前关于风电接入电网后的CPS研究内容较少，国内外对CPS的研究主要围绕以下2个方面：基于CPS的自动发电控制（AGC）策略，即研究适用于AGC的CPS考核逻辑，完善系统的AGC性能［5-7］；探讨CPS的理论机理，如文献［8］分析CPS统计特性和物理特性，阐述了CPS的数学原理，文献［9］从理论机理上分析了CPS与其他评价标准之间的关系。

本文结合CPS的统计学原理，对风电并网后CPS考核指标的变化特性进行了深入研究，给出了详细的理论分析和公式推导，明确了CPS考核指标随风电并网容量的变化趋势。最后以一个两区域互联电网为例进行仿真分析，定量评估了风电接入不同容量区域下的CPS指标变化特性，同理论分析相印证。同时给出了风电不同的分布特性对CPS指标的仿真分析。

1 CPS

1.1 CPS1

CPS1主要是用来衡量区域控制偏差（ACE）对频率偏差恢复的贡献作用，CPS1考核指标通常是1min计算一次，然后以一个平行移动年作为周期求取平均值［10-12］，并要求有下式成立：

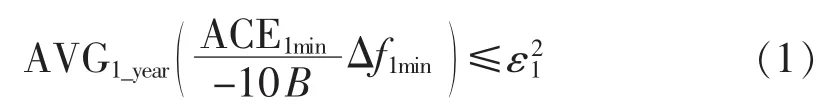
其中，AVG1_year（·）为以 1 a 为周期求平均值；ACE1min为控制区域1 min的区域控制偏差滚动平均值；Δf1min为控制区域1 min频率偏差的滚动平均值；B为控制区域的频率偏差系数（负数）；ε1为互联电网对全年1 min频率平均偏差的均方根的控制目标值，互联电网中，各个控制区域的ε1均相同。

CPS1考核指标的计算公式为：

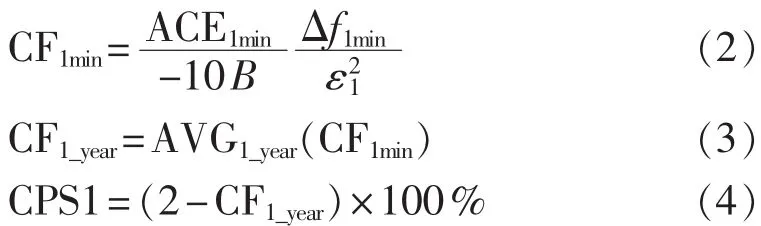
其中，CF1min为1 min服从因数；CF1_year为1 a的服从因数，根据CPS1考核标准，要求有CPS1≥100%，因此有 CF1_year≤1。

1.2 CPS2

CPS2主要侧重于功率控制，要求每10 min的区域控制偏差平均值在规定的范围L10以内［10-12］，如下式所示：

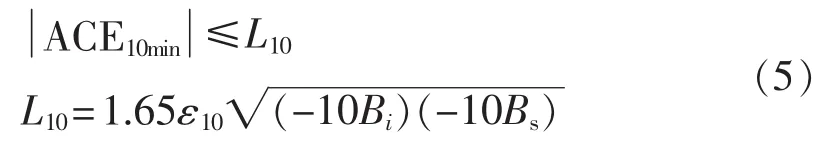
其中，ACE10min为10 min的区域控制偏差平均值；Bi为控制区域i的频率偏差系数；Bs为整个互联电网的频率偏差系数，即各控制区域中的频率偏差系数总和；ε10为互联电网对全年10 min频率平均偏差均方根的控制目标值。

CPS2考核指标的计算公式为：

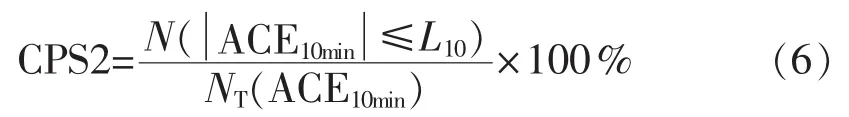
2 风电并网后对频率控制的影响

风电机组原则上具备参与系统一次调频的能力，且国外关于此方面的实例研究已取得了一定成果［13-15］，在我国，受能源政策主导，总体上仍然以风电的最大化输出和利用为目标［16-17］，国内风电机组基本上不参与实际系统调频。随着风电装机容量的不断增加，其逐步代替了部分具有调频能力的常规机组以后，将会对整个系统的调频能力产生重要影响，本文立足于国内风电发展现状，探讨了风电并网后对系统频率的影响。

2.1 风电并网后对系统自然频率特性系数的影响

假设系统额定总有功负荷为PLN，系统发电机组总额定容量为PGN，当风电没有接入电网时，根据电力系统的频率静态特性可知：

其中，β为系统的自然频率特性系数，KG为发电机组功频静特性系数，KL为负荷的频率调节效应系数。

将式（7）转换为标幺值，并整理后得到：

其中，kr=PGN/PLN为系统备用系数，带“*”变量为上述相应变量的标幺值。

风电并网以后对系统的自然频率特性系数的影响主要表现在如下2个方面［18-19］。

a.降低了电网等效的发电机组功频静特性系数KG*。当系统总容量一定时，随着风电装机容量的持续增加，必然会代替一部分常规发电机组，而当前大部分变速风力发电机组的输出功率与系统的频率是解耦的，因此风电机组基本上不具有频率响应能力。而具有一次调频能力的常规机组被代替以后，系统等效的发电机组功频静特性系数KG*将会减小。

b.降低了系统备用系数kr，考虑到风电的经济效益，通常风电机组不会被用来作为备用容量，而当系统的总容量一定时，随着风电并网容量的增加，常规机组的备用容量将会减小，而KL*只与负荷的特性有关，可以认为风电接入前后保持不变，因此根据式（7）、（8）可知，风电接入以后，系统的自然频率特性系数β*将会减小，而根据互联电网的频率偏差系数的选取原则，通常-10B的取值尽量等于或者接近自然频率特性系数β，因此风电接入以后，选取的频率偏差特性系数B也应该减小。

2.2 风电并网后对有功不平衡量的影响

互联电网在正常运行的情况下，其有功不平衡量主要是由于负荷的波动引起的，根据电网调度的短期负荷预测，其负荷不平衡功率可以定义为式（9）。

其中，PL为系统当前负荷，PL_fcst为调度预测的负荷。

当风电接入以后，由于其输出功率的随机性和波动性，将会导致系统有功功率不平衡［15］，根据调度部门对风电场输出功率的预测，定义风电不平衡功率为：

其中，PW为风电场当前出力，PW_fcst为调度预测的风电出力。

由式（9）和式（10），这里定义互联电网综合有功不平衡量为：

假设ΔPL和ΔPW相互独立，则系统综合有功不平衡量的方差D（·）可表示为：

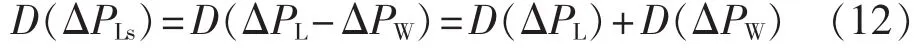
由式（12）可知，风电接入以后，系统的有功不平衡量的方差变大了。

2.3 区域控制偏差与有功不平衡量之间的关系

当互联电网产生了有功不平衡量ΔPLs，所有互联区域首先进行一次调频，根据一次调频结果有：

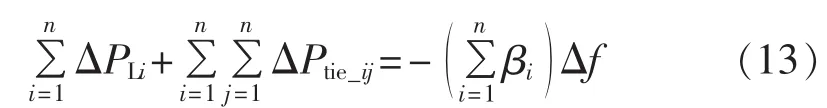
其中，ΔPLi为各个控制区域的有功不平衡量；βi为各个控制区域的自然频率特性系数；ΔPtie_ij为互联两区域之间的联络线交换功率；n为互联电网的控制区域个数。

由TBC模式下各个控制区域的区域控制偏差计算公式可知：

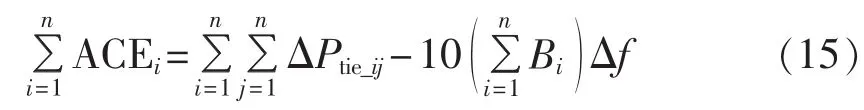
其中，ACEi为控制区域的区域控制偏差。

将式（14）代入式（16），并整理后得到：

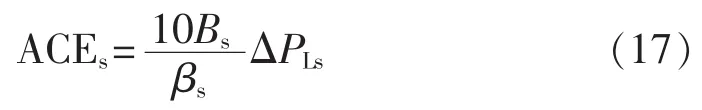
当前各大电网通常选取固定的频率偏差系数Bs，并且使Bs等于或者接近自然频率特性系数βs，因此，由式（17）可知，互联电网区域控制偏差与区域有功不平衡量具有比例关系。

3 基于统计理论的含风电的互联电网CPS研究

3.1 计及风电的互联电网CPS1研究

首先对CPS1进行一个统计分析，研究了风电并网以后，如何对互联电网控制区域的CPS1指标产生影响。假设在某一个时间段（t1，t2）内有：

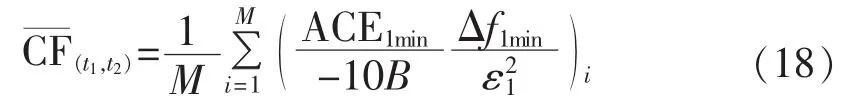
其中，下标 1min 表示各个变量的 1min 平均值；为（t1，t2）内的 CPS1 服从因数；M 为时间段（t1，t2）内的分钟数。

根据 CPS1 考核标准要求，为了在（t1，t2）时间内满足CPS1指标，则必须满足下式：

当时间段（t1，t2）足够大时，可以近似地认为：

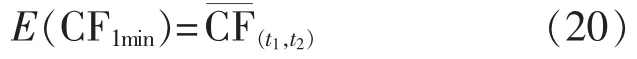
其中，E（·）为数学期望运算。

结合式（19）和式（20），一个等效的满足 CPS1指标的形式如下式所示：

根据式（2）可以得到：

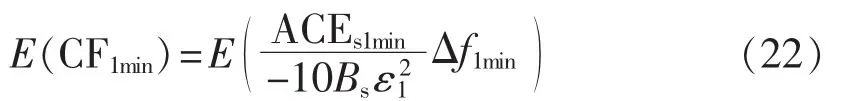
其中，ACEs1min为各控制区域偏差总和在1 min内的平均值。

将式（16）代入式（22）并整理后得到：

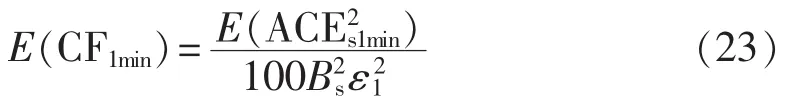
假设 E（ΔPLs）=0，根据式（17）可得：

根据方差的性质有：

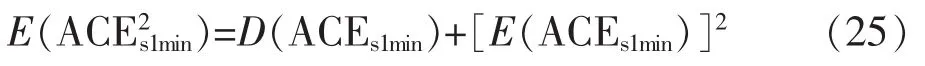
因此由式（23）—（25）可以得到：

根据式（12）和式（17）可知，D（ΔPLs）增大，D（ACEs1min）增大，而风电接入导致了系统自然频率响应系数减小，根据互联电网频率偏差系数的选取原则，Bs减小。因此根据式（26）可得 E（CF1min）增大。根据CPS1考核指标计算式（4）有：

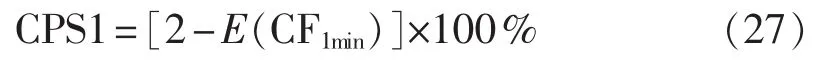
根据式（27）可知，风电并网以后，恶化了控制区域的CPS1考核指标，从而降低了互联电网的频率控制性能。如果不采取控制措施，会进一步影响系统吸纳风电的能力。

3.2 计及风电的互联电网CPS2研究

根据CPS2考核指标要求，每个10 min的区域控制偏差平均值在规定的范围以内，并且CPS2指标要求达到90%，根据式（6），如果统计的时间比较长，则NT（ACE10min）数目越大，因此近似地认为只要有如下公式成立，可以等效地认为满足CPS2考核标准：

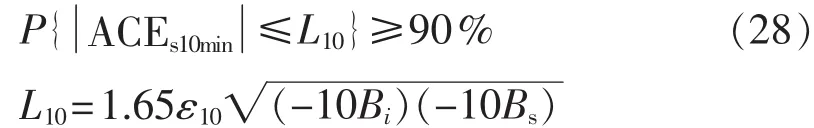
其中，ACEs10min为各控制区域偏差总和在10 min内的平均值，P｛·｝为概率运算。

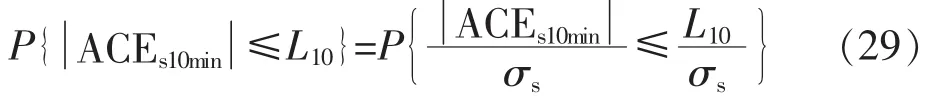
假设每个10 min的区域控制偏差采样点数为k，采样点记为 ACEsi（i=1，2，…，k），由于每个采样的ACEsi就是一个随机变量，并且有：

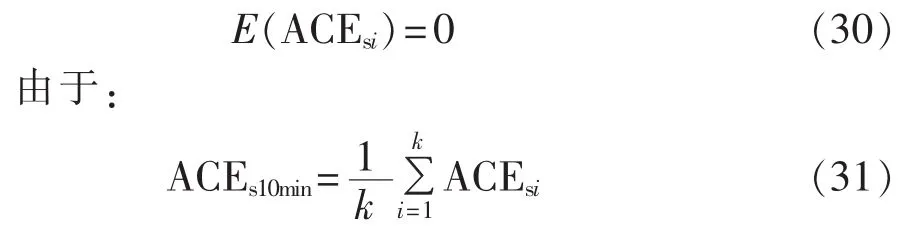
根据数学期望的性质有：

同时根据式（31）和式（32）可以得到：

因此根据中心极限定理有：

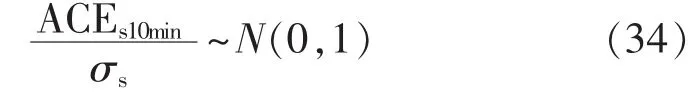
由标准正态分布可知：

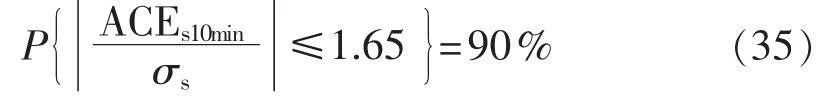
对比式（28）和式（35），可以得到，如果要满足CPS2指标，则必须有下列关系得到满足：

将L10与σs表达式代入式（36）并简化后得到：

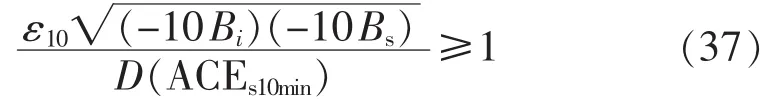
同理，风电接入以后，由于 D（ACEs10min）增大，频率偏差系数减小，互联电网能够满足式（37）的概率降低了，CPS2考核指标将会减小。系统的有功控制性能将会恶化。

4 仿真分析

以两区域火电互联电网为例（如图1所示），考虑2种不同比例的连接方式：方式A是2个区域具有相同的容量，运行特性相似，全部常规发电机组的装机容量为2000 MW，峰值负荷为1600 MW；方式B是区域1的装机容量、峰值负荷与方式A相同，保持不变，但是区域2的装机容量、峰值负荷变为原来的5倍，在方式B下，区域2的装机容量变为10000 MW，峰值负荷变为8000 MW。考虑在区域1中接入不同容量的风电，分析互联电网CPS考核指标的变化情况。仿真时间为12 h，并统计整个互联电网的CPS指标，为了便于分析比较，以风电穿透功率为0时的值作为基准，对不同风电穿透功率下CPS指标值进行标准化处理，即：

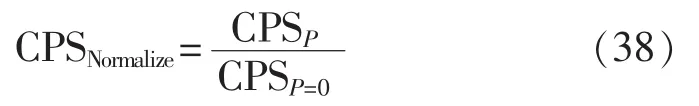
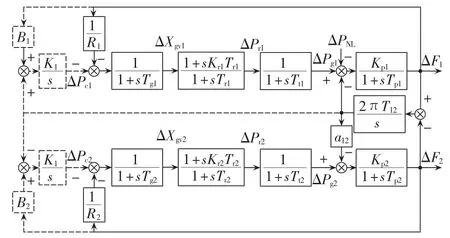
图1 两区域互联电网仿真模型Fig.1 Simulation model of two-area interconnected power grid

其中，P为风电穿透功率（%）；CPSP为在风电穿透功率为P时的CPS指标值，CPSP=0为风电穿透功率P=0时的CPS指标值。

具体参数选取如下：Tg1=Tg2=0.08 s，Kr1=Kr2=0.5，Tr1=Tr2=10 s，Tt1=Tt2=0.3 s，Kp1=Kp2=120，Tp1=Tp2=20 s，R1=R2=2.4，B1=B2=0.425，T12=0.086 6，ε1=0.022 Hz，ε10=0.018 Hz，K1=K2=0.7，在区域 1 接入不同容量的风电，互联在2种方式下，互联电网的风电穿透功率如表1所示。

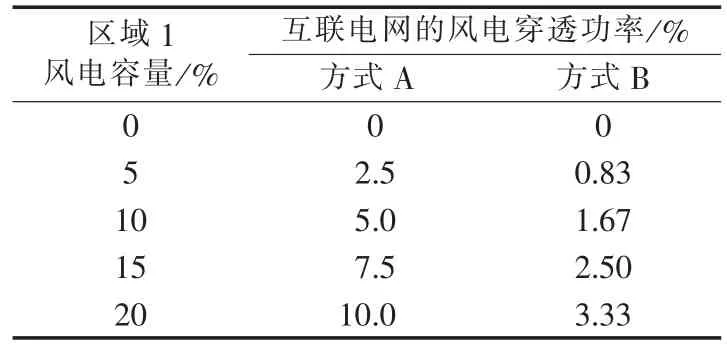
表1 风电穿透功率Tab.1 Wind power penetration levels

本文从统计理论的角度，计及不同风电分布特性，评估了风电接入电网后对CPS的影响（方式A），其中重点以正态分布、t分布以及威布尔分布为例开展了仿真研究，结果如图2、3所示。

以正态分布为例，考虑在不同容量电网区域接入风电，通过仿真分析不同比例的风电容量接入电网以后对互联电网CPS考核指标的影响情况。CPS1考核指标的仿真结果如表2所示。

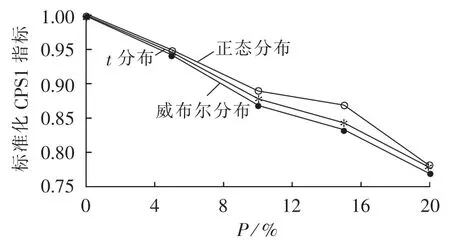
图2 风电功率的分布特性对CPS1指标的影响Fig.2 Impact of wind power distribution on CPS1 index

图3 风电功率的分布特性对CPS2指标的影响Fig.3 Impact of wind power distribution on CPS2 index

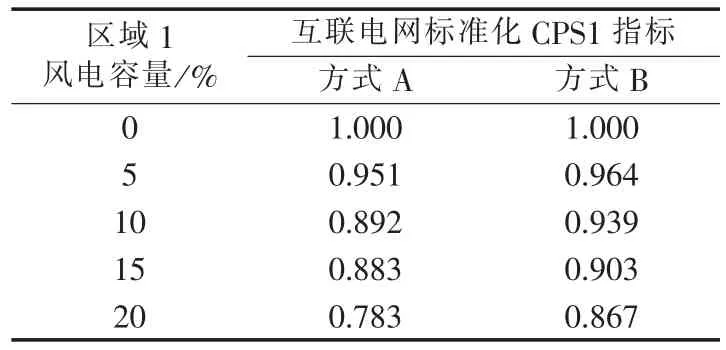
表2 CPS1仿真结果Tab.2 Simulative results of CPS1

从仿真结果可以看出，在区域1中接入不同容量的风电时，系统的CPS1指标呈下降趋势，与第3节分析结果相吻合，如图4所示。

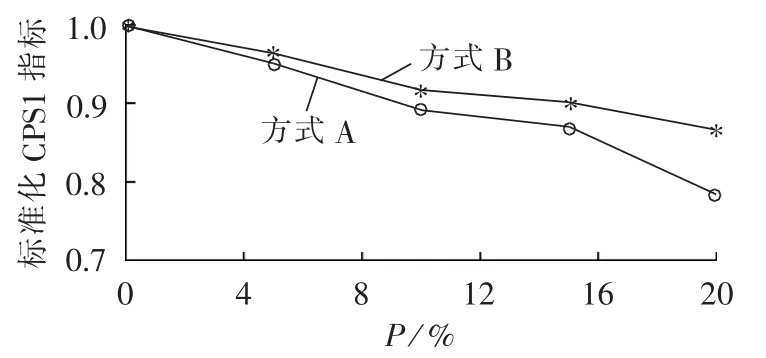
图4 CPS1考核指标变化情况Fig.4 Variation of CPS1 evaluation index

CPS2考核指标的仿真结果见表3。可见，CPS2指标也随着风电穿透功率比例的增大而降低，见图5。

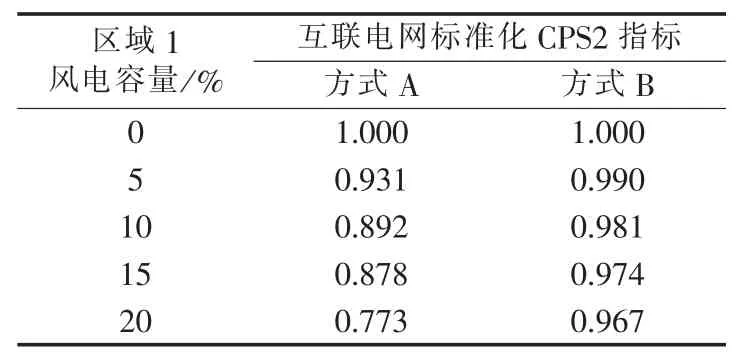
表3 CPS2仿真结果Tab.3 Simulative results of CPS2

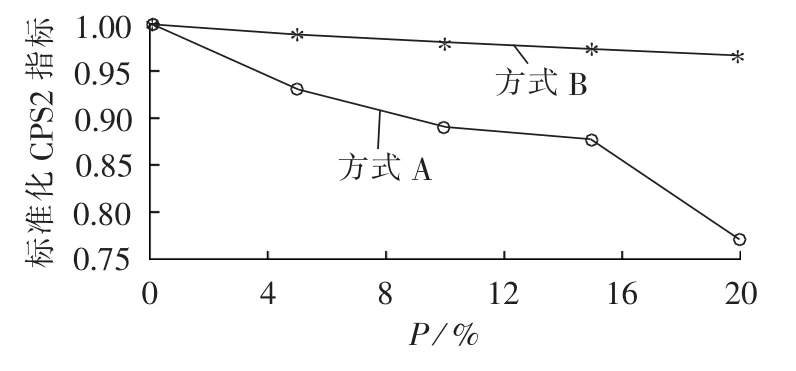
图5 CPS2考核指标变化情况Fig.5 Variation of CPS2 evaluation index

随着风电穿透功率的持续增大，系统的CPS考核指标将会恶化，表明系统的频率控制性能将会变差。当风电穿透功率超过某个阈值时，互联电网将会违背CPS考核标准。结合本文的理论分析和推导，初步给出一个确定风电穿透功率的新思路：以CPS1=100%和CPS2=90%作为门槛值，通过仿真分析，确定使互联电网的CPS1和CPS2考核指标等于门槛值时的风电穿透功率，此风电穿透功率即为该互联电网能够承受的最大风电容量比例。

5 结论

本文采用统计理论对风电接入系统后的CPS进行了研究分析，结合CPS的统计原理，进行了详细的理论分析和公式推导，分析结论表明CPS考核指标随风电并网容量的增大而减小。通过仿真分析得到如下结论：

a.针对风电不同分布特性对CPS的影响，基于所列举的3种典型分布，其对CPS的影响程度按由低到高排列分别为正态分布、t分布、威布尔分布；

b.不同容量的电网接入风电以后，CPS考核指标将会变差，且电网容量越小，CPS指标受影响程度越大，该仿真结果与理论分析相吻合。

受国家能源政策对风电发展的支持，风电并网规模日益庞大，而风电固有的随机性和波动性对电网CPS的影响逐渐显现出来，应给予重点关注。通过本文的分析，明确了风电对电网CPS影响的相关机理和因素，为后续开展多种能源协调控制以改善系统的CPS指标奠定了理论支撑，具备良好的参考及借鉴意义。