斜导面直线关节码垛机器人正运动学研究

周新云，李锻能 ，姚松亮，郑秀宏

ZHOU Xin-yun,LI Duan-neng,YAO Song-liang,ZHENG Xiu-hong

（广东工业大学 机电工程学院，广州 510520）

0 引言

串并混联的码垛机器人结合了串联机器人工作范围大的优点和并联机器人结构刚度大、承载能力强、运动精度高以及位置反解简单和力反馈控制方便的优点，适合码垛这种运行负载大、运动范围广的工作，逐渐成为了码垛机器人的一个研究方向[2～7]。机器人的正运动学是实现机器人闭环控制不可缺少的条件。目前，机器人正运动学求解的方法有：几何法、数值法、代数符号法及解的存在与证明等。

针对混联码垛机器人的结构，如图1所示，通过几何法，利用构造相似三角形的方法，快速的得到了码垛机器人的运动学正解。同时，工作空间范围也是机器人的一个重要指标，通过求解不同参数下的运动空间，证明了，这种求解方法，能够适应不同的工作范围。

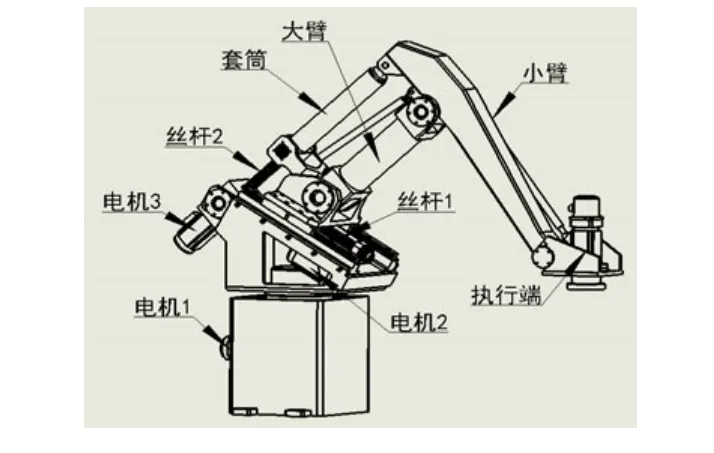
图1 码垛机器人实体

1 结构分析

目前码垛机器人从结构特点上可以分为两大类。一种是以ABB公司的IRB660为代表的传统串联关节型机器人，这种机器人的各个关节通过减速器与电机联接，构成所谓的串联机器人。另一种是以FUJI公司研制的Ace系列，主体结构应用了平行四边形机构，构成混联联机构，其驱动采用滚珠丝杆和滚动导轨这类线性驱动元件，依靠机构节点的水平与竖直的运动来实现末端执行器的合成运动[8]。

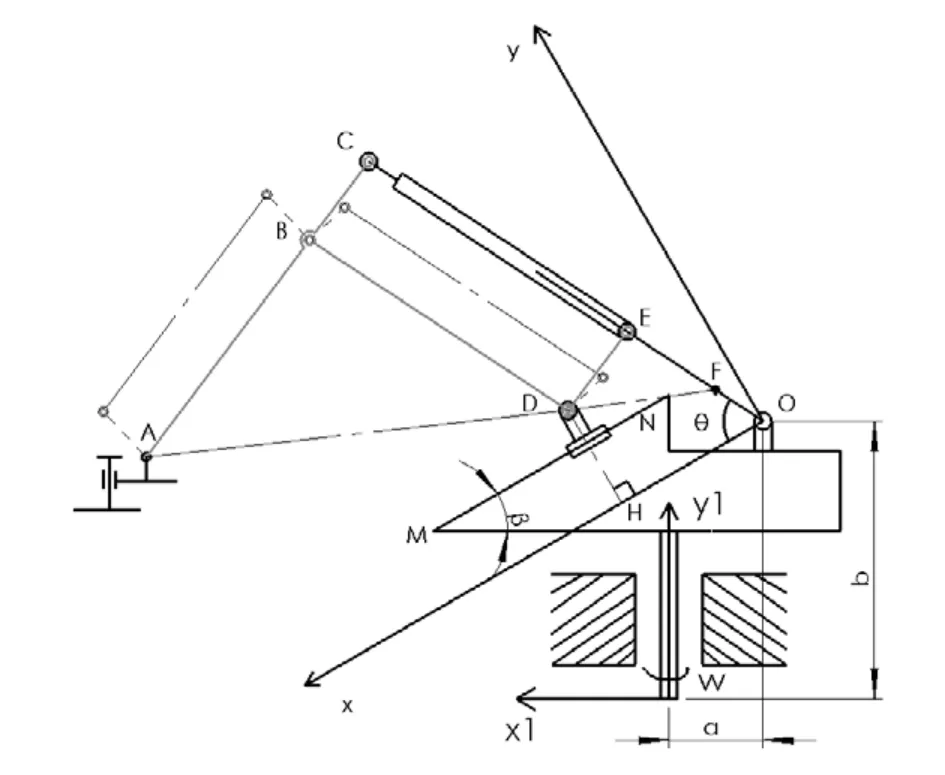
图2 码垛机器人机构简图

斜导面直线驱动混联码垛机器人类似于第二类机器人如图1所示，但不同的是下方驱动的导轨与水平方向保持一定的倾斜角β，这样可减小了斜道面丝杆轴向力的大小，使执行点的工作范围可变。同时上方驱动采用可以改变受力方向的丝杆套筒结构，及直线驱动，这样使得杆件的受力在一条直线上，驱动里传递效率最高，而且整个工作过程丝杆套筒处于受拉的状态，符合杆件合理受力方式。码垛机器人的机构图如图2所示。包括执行点A、小臂AC、大臂BD，同时构建以大臂小臂为边的平行四边形BDCE。OP为丝杆，CE为套筒，OP、CE构成丝杆套筒机构，电机1在O处驱动丝杆。D点在NM斜道面上滑动，D点由平行于NM的丝杆传动，由电机2驱动，整个斜面平台及其上部绕y1轴旋转，由电机3驱动。整个机构构成一个柱坐标。而执行端通过平行四边形机构保证其始终水平。

只考虑斜面平台上部的机构，可知杆件数n=6，低副个数Pl=8，高副个数Ph=0。

因此，自由度为：

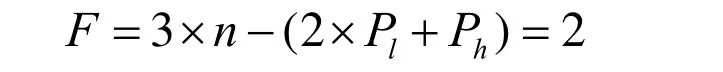
在斜面平台下方还有1个旋转自由度，因此，整个机构的自由度为3。

2 正运动学分析

根据斜导面式混联码垛机器人的机构特点，其机构的运动学求解时存在着耦合，本文提出了采用构造相似三角形的方式来推导其正运动学方程[9]。

首先，求机构在平面坐标系O-xy中执行点的坐标。

如图1所示，O、E、C在同一条直线上，此方向进给量由电机1以点O原点控制输入。

当OE=0时，此时：

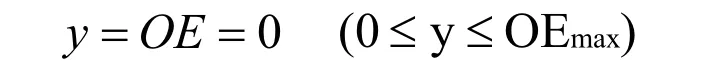
y为OE方向进给量。

设OE与x轴的夹角为θ；取OE上一动点F，使△FED ∽△DBA；则三角形相似比i：

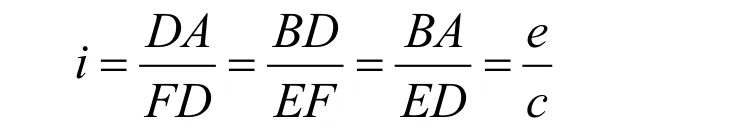
其中：BA=e，ED=c；可求出EF长度为：

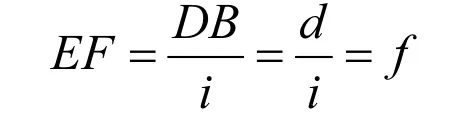
其中：EF=f，DB=d；即E，F点的坐标为：

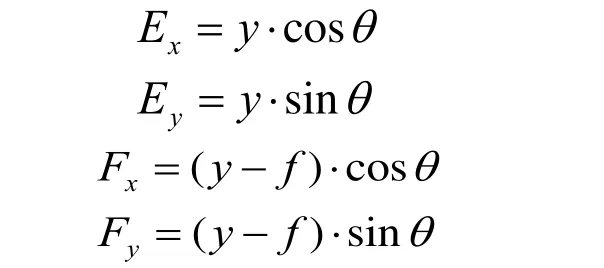
如图2所示，DH垂直于x轴于H。电机2驱动斜面丝杆，使导板D沿平行于x轴方向运动。

设，当H与O点重合时：

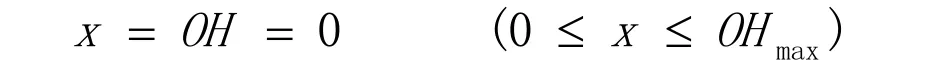
其中x为OH方向进给量；

则D点的坐标为：

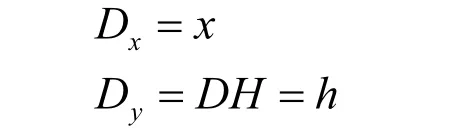
其中DH=h。

设A点坐标为Ax，Ay；由i=AD/DF ，则A点坐标为：

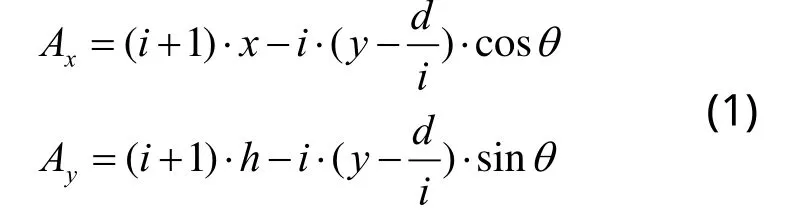
在式(1)中sinθ,cosθ 为未知数。

通过四边形OHDE可求得θ与x，y的关系。知ED=c，E点和D的坐标，运用两点间距离公式，即θ与x，y存在着如下关系：

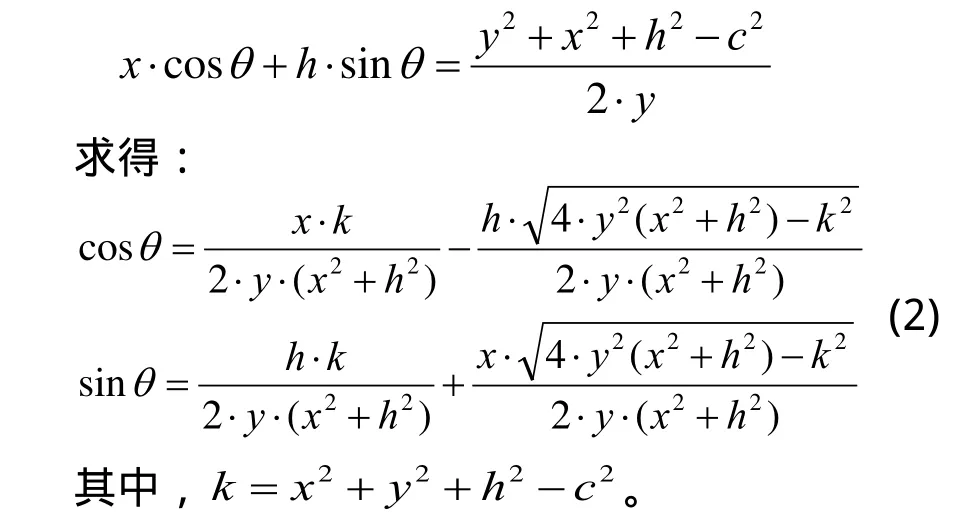
其次，求执行点A点在O-x1y1中的坐标，通过坐标变换，有A点坐标为：

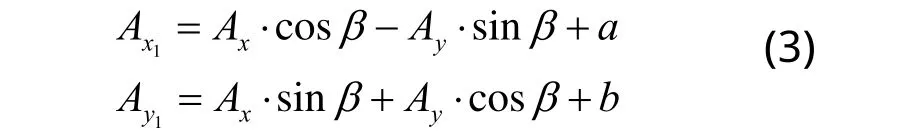
最后，求机构在空间坐标系中执行点与驱动量之间的运动学关系。

在平面坐标系O1-x1y1的原点处，过原点作坐标轴x2垂直于该平面，且z2轴取y1轴，y2轴取x1轴，由x，y，z轴构成空间直角坐标系。设电机3转动的角度为α。则空间坐标系O-x2y2z2中A点坐标为：

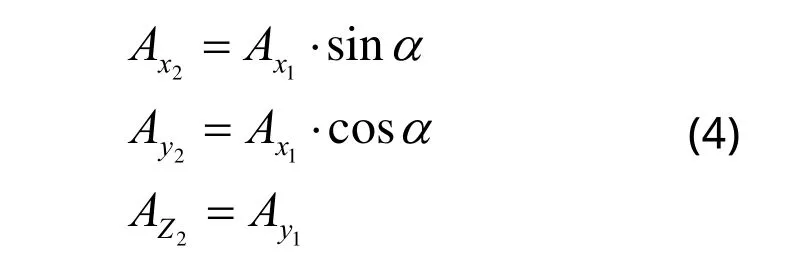
式（1）～式（4）式便是运动学方程的正解，当已知各关节的运动参数，便可求得末端执行器的位置。

确定电机1和电机2的运动范围：当取电机1的运动范围为[xmax,xmin]时，由△DOE三边的关系可知，y满足的条件为：

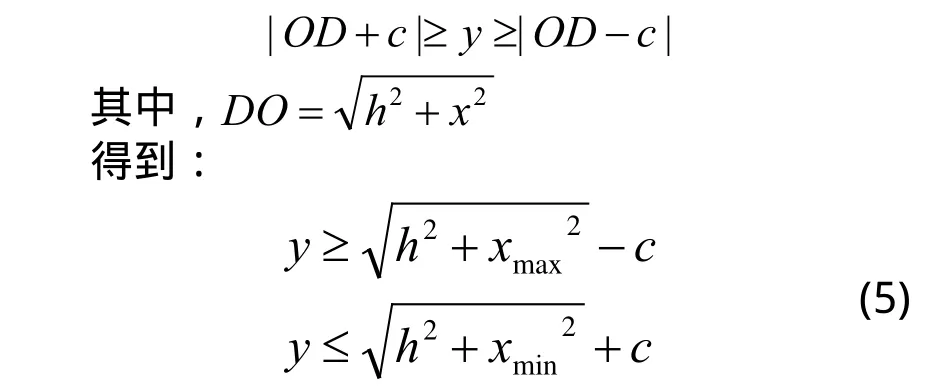
通过上面的推导,可以得出该机器人的运动学结论：码垛机器人执行点在x轴的运动与三个电机的驱动量有关；y轴的运动与三个电机的驱动量有关；z轴的运动与电机1和电机2的驱动量有关。本文研究的码垛机器人各轴相互耦合，运动学逆解无法通过上序求得的运动学方程求解。运动正解通过在OE上取动点F，构造相似三角形的方法，使码垛机器人运动学分析正向求解问题得到简化；同时，如果需要改变AB的杆长来增大工作空间，以上的运动学分析依然成立。这样使这种码垛机器人的应用更灵活。这种方法也可以应用于其他类似的机器人运动学求解。

3 工作空间分析

机器人的工作空间是指其末端能够到达的空间点的集合，它是机器人学中一重要的研究领域，是评价机器人几何特性的重要指标。另外，机器人的结构参数主要根据末端参考点所要求达到的工作区域来确定，因此工作空间的分析显得非常重要。

由于码垛机器人的运动空间为一个柱坐标，因此这里只分析在O-xy平面的运动轨迹和运动范围，根据上节求出的运动方程，运用MATLAB，先分析单独驱动作用下的运动轨迹；然后，分析在倾斜角β取不同值时的工作平面的位置；最后，分析在整体机构不变的情况下改变AB杆长来求得工作平面的位置。

给定参数值：取电机1运动范围为x=[180,340]，相关参数：a=233，b=540，c=150，d=350，e=300，h=142，β=30 。则由式（5）得：电机2的运动范围为[209,379]。取本码垛机器人电机2的运动范围取[220,370]。

电机1单独驱动时的运动轨迹：当电机2处于y=220、y=270、y=320、y=370这四个位置，电机1给进,得到执行端在Ox1y1平面的运动曲线如图3所示。

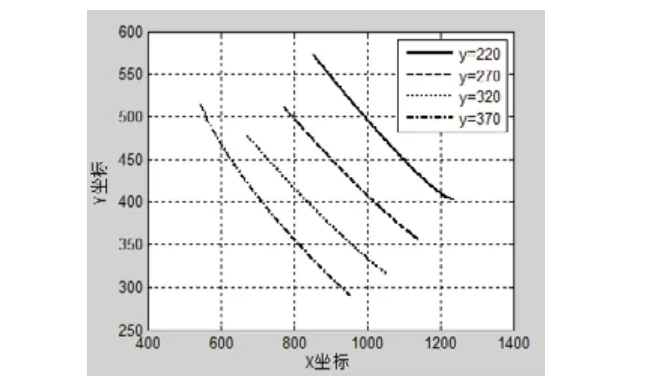
图3 电机1单独驱动时的运动曲线（β=30 ）

电机2单独驱动时的运动轨迹：当电机1处于x=180、x=230、x=280、x=340这四个位置，电机2给进时,得到执行端在Ox1y1平面的运动曲线如图4所示。

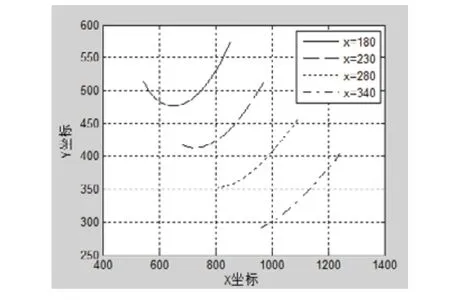
图4 电机2单独驱动时的运动曲线（β=30 ）

由图3、图4可知码垛机器人各轴的运动都是非线性的，且各轴都相互耦合。

在倾斜角β取不同值时码垛机器人在过z轴的平面的位置：当AB=500，分别取β=0 ，β=30 时码垛机器人在过z轴的平面上的最大工作范围如图5所示。

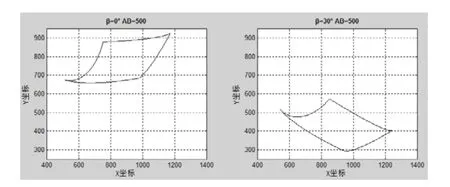
图5 不同β值下运动平面仿真结果

由图5可知，与β=0 相比，β=30 时，将工作平面绕图1的O点旋转了一个30 ，使得工作空间整体下移。

在AB杆长取不同值时码垛机器人在过z轴的平面的位置：当β=30 ，取AB=500和AB=700时码垛机器人在过z轴的平面上的最大工作范围如图6所示。

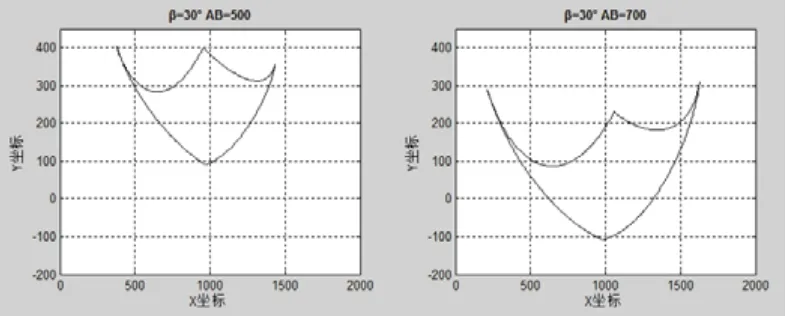
图6 不同AB杆长下的运动平面仿真结果

由图6可知，当倾斜角β不变时，通过增加AB杆的长度，会使码垛机器人在过z轴的平面上的工作范围下移，并且工作范围增大。这样，在系列产品设计中，可通过改变AB的杆长，来设计出不同工作范围的码垛机器人，同时，由于AB杆长不同的码垛机器人，在运动算法上相同，无需大幅度的改变结构，有利于产品的系列化。

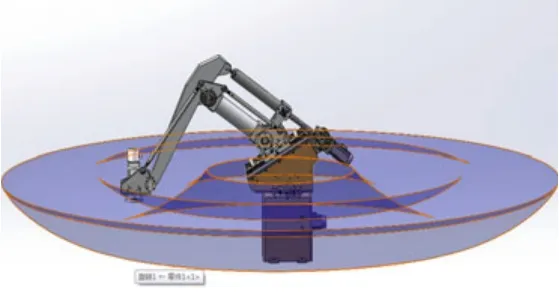
图7 码垛机器人的工作空间

文章最后运用Solidworks的插入->曲线->通过XYZ点的曲线，来将码垛机器人在过z轴的平面上的最大工作范围的边界点导入到Solidworks中，同将工作平面绕x轴旋转一周，得到码垛机器人在参数AB=500，β=30 时的工作空间，如图7所示。

4 结束语

本文针对一种新型斜导面式码垛机器人的运动学进行了分析和研究，采用了巧妙的构造相似三角形的方法来求得运动学方程。运用Matlab分析了电机1和电机2单独驱动时的运动轨迹。采用这种斜导面形式，采用一个角度β可变的变量设计法，可以的码垛机器人的运动空间范围进行优化，增加了码垛机器人的灵活性。

[1] 李成伟,朱秀丽,贠超.码垛机器人机构设计与控制系统研究[J].机电工程,2008,25(12):81-99.

[2] SpiessJ.Development of high capaeity bagging and palletizinglines . World Cement.1995,26(12,2):52-53.

[3] Hingson Erie.Palletizing robots for the consumer goods in ustrylndustrial Robot,1998,25(6):34-38.

[4] Er1eH.Palletizing robots for the consumer goods industry.Industrial Robot.1998(6):34-38.

[5] GeorgeA,WeiMerIV.New robotics technology adds value to material handling.Palletizing Material Handling Engineering,1998(6):61-62.

[6] 曲云霞,李为民.并联机构构型概述[J].机械加工工艺与装备,2007,(2):48-51.

[7] 马晓丽,陈艾华.并联机器人机构的创新与应用研究进展[J].机床与液压,2007,(2):23-237.

[8] 尹春娜.混联码垛机器人机构选型设计及最大工作空间分析[J].机电产品开发与创新,2010,24(1):18-20.

[9] 李晓刚,刘晋浩.码垛机器人的研究与应用现状、问题及对策[J].包装工程,2011,32(3):100.

[10] 张曙.并联运动机床1版[M].北京:机械工业出版社,2003:8-17.

[11]徐金明.MATLAB实用教程2版[M].北京:清华大学出版社,2005:174-178.