基于混合误差迭代学习控制的XY平台轮廓控制

王丽梅，郭宜兴

WANG Li-mei,GUO Yi-xing

（沈阳工业大学 电气工程学院，沈阳 110870）

0 引言

数控机床正在向精密、高速和复合化的方向发展。轮廓精度和位置跟踪能力已成为多轴进给系统的两个重要指标[1]。传统数控机床的直线运动是由电动机的旋转运动通过机械设备转化而来，然而由于机械设备在传动过程中不可避免的会产生摩擦和弹性形变等不利因素，因此，直线电机被应用到数控机床中[2]。但是，由于直线电机是一个多变量和时变的非线性系统，传统的PID控制器已经很难实现精确控制[3]。虽然自适应控制、鲁棒控制、神经网络控制和滑模控制等方法可以获得较好的输出效果，但是它们都要求有精确的模型对象，当模型不准确，或者参数发生变化时，就无法实现精确的位置跟踪[4～9]。而迭代学习控制器不仅不要求有精确的被控对象模型，而且在模型参数变化时，通过学习，仍然可以实现高精度位置跟踪，文献[10]实现了迭代学习控制直线电机的高精度位置跟踪。文献[11]在XY平台各轴上实现了迭代学习控制的应用，但是没有考虑两轴的不匹配问题。

针对系统存在的负载扰动、XY轴动态响应不一致，本文采用基于实时轮廓误差模型与迭代学习控制相结合的控制策略对XY平台进行轮廓和位置控制。为了提高系统响应速度，使系统具有鲁棒性，单轴采用IP与ILC控制器相结合的方法。现有的交叉耦合控制器和基于局部任务坐标系的轮廓运动控制器等都利用各轴的位置误差来估计轮廓误差，这些方法成立的一个前提是位置误差远小于期望轮廓的曲率半径[12～14]，而在迭代学习初期，各轴位置误差都比较大，用轮廓误差来修正控制信号已经没有意义，因此，本文提出基于混合误差的迭代学习控制，在迭代初期只用位置误差修正控制信号，而当位置误差减小到一定程度后，再用轮廓误差修正控制信号，最终使系统达到轮廓加工的高精度要求。

1 双轴平台的实时轮廓误差模型

对于直线电机驱动XY平台，由两台永磁直线同步电动机直接驱动两轴相互垂直的XY平台。其机械运动方程为：

其中，x(t)为动子的位移，iq为动子q轴电流，Kf为推力系数，Fe为电磁推力，M为动子及所带负载的总质量，B为粘滞摩擦系数，F为外部扰动。

在连续轨迹控制系统中，XY双轴平台系统不仅对单个轴的运动速度和精度控制有严格要求，而且在双轴联动时，还要求各移动轴有很好的动态配合，因此，系统的单轴位置误差与轮廓误差对轮廓加工精度有较大的影响。而对于自由形态的跟踪任务中，轮廓误差模型的精度将直接影响轮廓加工的性能。综上，建立实时轮廓误差模型如图1所示。

图1 实时轮廓误差

其中，R1为指令路径，P1为实际路径，R1(t)为指令位置点，P1(t)为实际位置点，而R2(t)是指令路径上距离P1(t)最近的一个点，L为当前跟踪误差Ep在点P1(t)处的切向投影，R2(t)点与R1(t)点的长度约等于L，而轮廓误差定义为实际位置与给定指令位置的最短距离，即为E'c，因此，自由形态轨迹跟踪任务中的轮廓误差可以利用P1(t)与R2(t)之间的距离来计算，即：

其中，Ex与Ey分别为系统跟踪误差Ep在XY轴的分量，j为通过R2(t)与R1(t)的直线与X轴的夹角为：

其中，R2x(t)和R2y(t)分别为R2(t)在XY轴上的分量，R1x(t)和R1y(t)分别为R1(t)在XY轴的分量，R2(t)可计算为：

式中，V1x(t)，V1y(t)分别为R1(t)点在XY轴的切向分量速度，V2x(t)，V2y(t)分别为R2(t)点在XY轴的切向分量速度，Vx(t)和Vy(t)分别为系统X轴和Y轴的进给速度，计算为：

通常平台系统的进给速度并不是常值，所以，V2x(t)，V2y(t)的值不能准确求出。那么假设R2(t)与P1(t)有相同的切向速度，那么上述方程可以重新给出：

综上，将式(4)、式(5)、式(8)和式(9)带入到式(3)中即为轮廓误差的数学模型。

2 单轴控制器设计

2.1 位置跟踪迭代学习控制器的设计

图2为XY平台系统单轴位置跟踪迭代学习控制框图。其中，Φ为迭代学习控制器学习增益，yr为y轴的期望位置，yj+1为系统进行第j+1次迭代时的位置输出，P为被控对象，uj和uj+1分别为第j次和第j+1迭代的控制信号。第j次的控制信号uj存到存储器里，并在第j+1次迭代时，构造出新的控制信号uj+1。系统的位置误差被ILC控制器处理后，得到的新控制信号，下一次迭代时，再反馈给系统，通过不断的学习，位置误差得到不断的减小。

图2 位置跟踪迭代学习控制框图

定义位置跟踪迭代学习的学习律为：

其中，f(z)为学习增益，为了突出系统的快速响应能力，本文采用PD型闭环迭代学习控制律，φ(z)为：

这里kp、kd和Ts分别是比例增益、微分增益和采样周期。

误差ej+1定义为：

将跟踪误差和控制信号动态方程改写为：

由压缩原理得出，系统收敛的条件为：

2.2 IP控制器设计

迭代学习控制器有一定的滞后性，因此，本文在XY平台的单轴位置控制器采用带速度前馈的IP控制器结构来提高系统的响应速度，增强系统的抗扰动能力，保证闭环系统具有较强的鲁棒性。设计单轴控制器如图3所示。

图3 加入IP控制器的单轴控制器框图

由图3可知速度环的传递函数为：

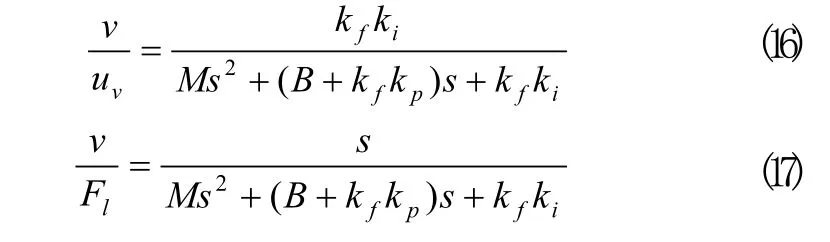
由式(16)可知，增大ki可提高系统的响应速度，由式（17）可以看出，增大ki相当于增强系统抗扰动能力。为补偿时间延时对XY平台系统跟踪精度的影响，加入速度前馈控制器降低系统的位置误差，保证了系统响应的快速特性。

未加入速度前馈时，单轴的传递函数为：

加入速度前馈后的传递函数为：

如式(18)和式(19)，加入速度前馈后,系统增加了一个零点,从而增加了系统的频宽，提高了系统的响应速度。

3 轮廓控制器设计

轮廓误差迭代学习控制就是将迭代学习控制应用到轮廓误差模型中，使系统在前一次的迭代中学习纠正系统中存在的负载扰动以及各轴响应速度不一致等各种不确定性。图4为轮廓误差迭代学习控制器。其中，ux,j+1、uy,j+1、ux,j和uy,j分别为X、Y轴在第j+1次和第j次迭代时的控制信号；xj+1、yj+1分别为X、Y轴在第j次迭代时的位置输出；Exc、Eyc分别为轮廓误差在X轴和Y轴的分量，可以由式(3)、式(4)、式(5)、式(8)和式(9)得到。轮廓误差的学习律为：

由式(21)可以看出，前一次迭代的控制信息和当次迭代的轮廓误差用来更新系统的控制信号，式中：

如图4所示为直线电机XY平台的系统框图。

图4 混合误差迭代学习控制器框图

图中，k1、k2分别为混合误差迭代系统的转换开关；因此，将轮廓-位置误差迭代学习律改写为如下形式：

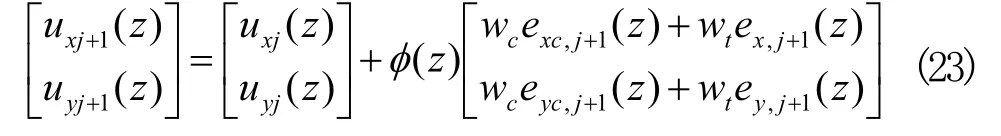
式中wc、wt分别为开关k1、k2的转换因子，其分别代表轮廓误差转换因子和位置误差转换因子，其值可选为0或1。当转换开关k1闭合，k2断开，即wc=0，wt=1时，用各轴位置误差更新控制信号；当转换开关k2闭合，k1断开，即wc=0，wt=1时，则用轮廓误差更新控制信号。本文用每次迭代的位置误差来判断用哪种误差更新控制信号，当位置误差小于10μm时用轮廓误差更新控制信号，反之用位置误差更新控制信号。

4 仿真与分析

本文仿真采用日本Yokogawa LM110系列直线电机驱动XY平台进行仿真研究，其参数分别为M1= 4.4kg，M2= 1.4kg，Kf1= 10.9794N/A，Kf2=8.526N/A，B1=244.3192Ns/m，B2=82.0176Ns/m。指令路径为长轴长为a=0.05，短轴长为b=0.04的椭圆形，即两轴输入指令为xr(t)=0.05sinðt ，yr(t)=0.04cosðt 。

前馈控制器系数kv1、kv2为1；X轴的IP控制器的积分、比例增益分别为125、20.523，迭代学习控制学习增益Kp、Kd分别为30.21、9.32；Y轴的IP控制器的积分、比例增益分别为100、39.354，迭代学习控制学习增益Kp、Kd分别为50.698、10.324。为了验证系统的抗干扰能力，在t=2.5s时突加50N的干扰力，采样时间设为0.001s。通过Mat1ab7.10进行仿真，得到仿真曲线如下。

图5 椭圆指令轨迹与输出轨迹

图6 X、Y轴最大位置误差

图7 椭圆轨迹的轮廓误差曲线

图5为外部扰动和系统不确定性均存在时，XY平台的期望输入与实际输出轨迹曲线，可以看出，在本文提出的控制策略作用下，指令轨迹与实际轨迹基本重合。图6为X、Y轴的在迭代轴上的位置误差曲线，随着迭代次数的增加，迭代学习控制器不断修正控制信号，实际输出位置不断接近期望位置，在迭代到第九次的时候，位置误差达到稳定状态。图7为外加扰动作用，跟踪各轴位置误差和混合误差情况下，XY平台迭代15次后的轮廓误差曲线，可以看出，无论在有无扰动情况下，跟踪混合误差时的轮廓误差均小于跟踪位置误差情况下的轮廓误差，跟踪混合误差时，轮廓精度有明显提高。

5 结论

本文采用适用多轴轮廓控制的轮廓误差计算法则计算轮廓误差，对XY平台系统进行控制。通过在单轴上结合IP控制器与跟踪位置误差迭代学习控制器有效地抑制了负载扰动对系统的影响，保证了系统的鲁棒性，速度前馈控制提高了响应速度，提高了系统的跟踪性能。轮廓控制采用基于实时轮廓误差模型的混合误差迭代学习控制器，削弱了由于双轴速度不匹配对轮廓精度的影响。仿真结果表明所设计的控制系统有效地提高了XY平台的轮廓加工精度。

[1] 郭庆鼎,王成元,周美文,等.直线交流伺服系统的精密控制技术[M].北京∶机械工业出版社,2000.

[2] 唐振宇.直线电机进给驱动技术在数控机床上的应用[J].机床与液压,2009,37(6)∶62-64.

[3] 张宏伟,余发山,卜旭辉,王福忠.基于鲁棒迭代学习的永磁直线电机控制[M].电机与控制学报,2012,16(6)∶81-86.

[4] 鲁文其,胡育文,梁骄雁,黄文新.永磁同步电机伺服系统抗扰动自适应控制[J].中国电机工程学报,2011,31(3)∶75-81.

[5] 王立标,李军,范剑,李绣峰.基于自适应DRNN的无刷直流电机控制方法研究[J].中国机械工程,2011,22(19)∶2237-2240.

[6] 杨书生,钟宜生.永磁同步电机转速伺服系统鲁棒控制器设计[J].中国电机工程学报,2009,29(3)∶84-90.

[7] 党选举,徐小平,于晓明,姜辉.永磁同步直线电机的小波神经网络控制[J].电机与控制学报,2013,17(1)∶43-50.

[8] 王丽梅,武志涛,左涛.永磁直线电机自构式模糊神经网络控制器设计[J].电机与控制学报.2009,13(5)∶643-647.

[9] Faa-Jeng Lin,Jonq-Chin Hwang,Po-Huan Chou,Ying-Chih Hung.FPGA-Based Inte11igent-Comp1ementary S1iding-Mode Contro1 for PMLSM Servo-Drive System[J].IEEE Transactions on Power E1ectronics,2010,25(10)∶2573-2587.

[10] 石阳春,周云飞,李鸿,李介明,黄永红.长行程直线电机的迭代学习控制[J].中国电机工程学报,2007,27(24)∶92-96.

[11] Jian-Xin Xu,Sanjib K. Panda,Tong H. Lee.Rea1-time Iterative Learning Contro1 Design and App1ications[M].London∶Springer-Ver1ag,2008.

[12] Yang J,Li Z.A nove1 contour error estimation for Position 1oop-based cross-coup1ed contro1[J].IEEE/ASME Trans.on Mechatronics,2010,16(4)∶643-655.

[13] Chu-xiong Hu,Bin Yao,Qing-feng Wang.Coordinated adaptive robust contouring contro11er design for an industria1 biaxia1 precision gantry.IEEE/ASME Transactions on Mechatronics,2010,15(5)∶728-735.

[14] Bin Yao,Chu-xiong Hu,Qing-feng Wang.An Orthogona1 G1oba1 Task Coordinate Frame for Contouring Contro1 of Biaxia1 Systems[J].IEEE/ASME Transactions on Mechatro nics,2012,17(4)∶622-634.