改进粒子群算法在紧固螺母路径中的优化

陈 震，彭先涛

CHEN Zhen1，PENG Xian-tao2

(1.泰州职业技术学院 信息工程学院，泰州 225300；2. 辽宁石油化工大学 信息与控制工程学院，抚顺 113001)

0 引言

装配生产线上紧固螺母路径优化问题是在一条装配线上用一个机械手去紧固待装配部件上的螺母问题。机械手由其初始位置开始，依次移动到其余的每一个螺母，最后返回到初始的位置。机械手的运行轨迹就是以螺母为节点的一条周游路线。优化之前，机械手的运行轨迹是随机的，完成一块板子的装配耗时过长，使得生产效率低下，产品的成本较高，竞争力低下。因此工艺上要求机械手运行时间尽可能短，需要对机械手的运行轨迹进行优化，从而使机械手完成对该配件的装配总时间最小。该问题的最优解就是寻找机械手在螺母间的最短运行路径，此时，该问题可以转换为TSP问题。由此可见，该问题也是典型的多项式复杂程度的非确定性问题(Non-deterministic Polynomial的问题，NP问题)，即其最坏情况下的时间复杂度随着问题规模的增大按指数方式增长，该问题的答案是无法直接计算得到的，只能通过间接的“猜算”来得到结果，到目前为止还没有找到一个多项式时间的有效算法[1]。

1 解决方法的提出

目前这类问题的解决方法主要有：近邻法、插入法、禁忌搜索算法[2]、遗传算法[3]、模拟退火算法[4]等等。但以上方法各存在一些问题，近邻法简单，也许是多数人的直觉做法，但是近邻法的短视使其表现非常不好，通常后段的路程会非常痛苦；插入法中点的选择及法则的选取较繁琐，且计算量大，前期的工作量很大，有先苦后甜的滋味；禁忌搜索算法是一种局部搜索能力很强的全局迭代寻优算法，不足之处在于对初始解较强的依赖性和串行的迭代搜索过程[5]；GA两个最显著的优点是隐含并行性和全局解空间搜索，但实际应用时易出现早熟收敛和收敛性能差等缺点[4]；模拟退火算法突出地具有脱离局域最优陷阱的能力，实验性能具有质量高、初值鲁棒性强、通用易实现的优点，最大缺点是往往优化过程较长[5]。

粒子群优化算法(Particle Swarm Optimization ，PSO)是一种基于群体智能的新兴演化计算技术[6]，广泛用于解决科学研究和工程实践中的优化问题。PSO通过粒子追随自己找到的最好解和整个群的最好解来完成优化。该算法简单易实现，可调参数少，已得到广泛研究和应用。PSO算法求解优化问题时，算法中每个粒子都代表问题的一个潜在解，每个粒子对应一个由适应度函数决定的适应度值，问题的解对应于搜索空间中一个粒子(或称为主体)的位置，每个粒子都有自己的位置和速度(决定自身飞行的方向和距离)。各个粒子记忆、追随当前的最优粒子，在解空间中搜索。每次迭代的过程不是完全随机的，如果找到较好解，将会以此为依据来寻找下一个解[7～9]。PSO的优点是简单且易于实现，没有许多参数需要进行调整[3]。

PSO算法有全局版本和局部版本，这两个版本的差别在于粒子的邻域不同，研究发现，全局PSO算法收敛较快，但易陷入局部最优，而局部PSO算法可搜索到更优的解，但速度稍慢。可见算法选择的领域不同，会对算法的性能有很大的影响。同时基本PSO算法局部搜索能力较差，搜索精度不高，不能保证搜索到全局最优解；随着迭代次数的增加，当种群收敛集中时，各粒子也越来越相似，容易陷入局部最优解而无法跳出；对参数有一定的依赖性等不足之处[11]。因此，对PSO提出改进，以提高PSO的搜索能力具有很高的研究意义，一些成果可参考文献[10]。本文采用将GA[11]与PSO相结合得到的GA-PSO对该问题进行优化：摒弃传统PSO中通过跟踪极值来更新粒子位置的方法，引入GA中的交叉和变异操作，通过粒子同个体极值和群体极值的交叉、粒子自身变异的方式来搜索最优解。仿真结果表明改进的PSO能够很好的跳出局部极小值，较快地寻找到机械手的最优运行路径。

2 GA-PSO

本文采用GA-PSO实现紧固螺母路径优化问题的具体步骤如下：

1)种群初始化：初始产生1000个粒子。

2)个体编码：粒子个体编码采用采用整数编码，每个粒子表示历经的所有螺母，如当经历的螺母数为9，个体编码为[5 9 3 6 7 2 1 4 8]，表示螺母遍历从5开始，经过9，3，6，7，2，1，4，8，最终返回螺母5，完成TSP遍历。

3)计算适应度值

适应度值表示为机械手遍历路径的长度，按公式（1）进行计算，其中Li,j为螺母i，j间的距离。

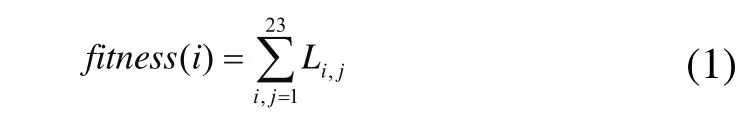
4)粒子的更新：粒子的速度和位置按式（2）、（3）进行更新：

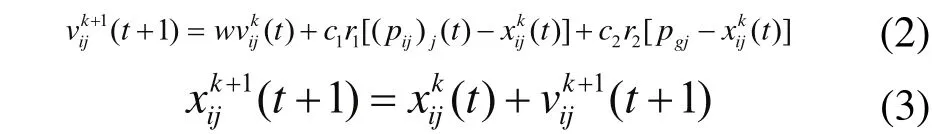
5)交叉操作：交叉操作包括个体最优交叉(个体与个体极值交叉更新)和群体最优交叉(个体与群体极值进行交叉更新)，交叉操作采用整数交叉法。先选择两个交叉位置，然后分别进行个体最优交叉、群体最优交叉，假定随机选取的交叉位置为2和4，操作如下：

产生的新个体如果存在重复位置则对其进行调整，采用的调整方法为用个体中未包括的螺母代替重复包括的螺母，具体如下：

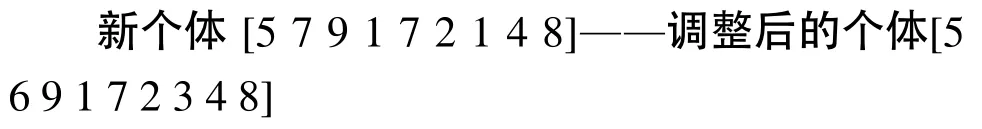
6)粒子变异操作：变异操作采用个体内部两位互换法，先随机选择两个变异位置，然后把两个变异位置进行互换，如假定选择的变异位置为3和6，变异操作如下：

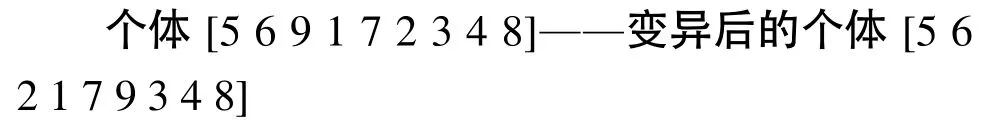
同时对得到的新个体采用了保留优秀个体的策略，只有当新离子适应度值好于旧粒子时才对粒子进行更新。

7)判断算法是否结束：算法结束条件为迭代200次。

3 GA-PSO仿真研究

本文以浙江宁波某汽车配件厂某条流水线上的某型号配件上的螺母固定为研究对象，数据如图1所示。

图1 螺母坐标数据

机械手在每个螺母上停留的时间为4s(机械手移动到待固定的螺母上方、对螺母进行固定、离开螺母的总时间)，机械手在螺母间的运动速度为匀速(5cm/s)。对该问题进行优化得到的目标是使机械手在对该配件上所有螺母进行固定后的总时间最小，也就是使机械手在该配件上所有螺母间的移动路径最短。

本文改进的粒子群算法(GA-PSO)的流程图如图2所示。

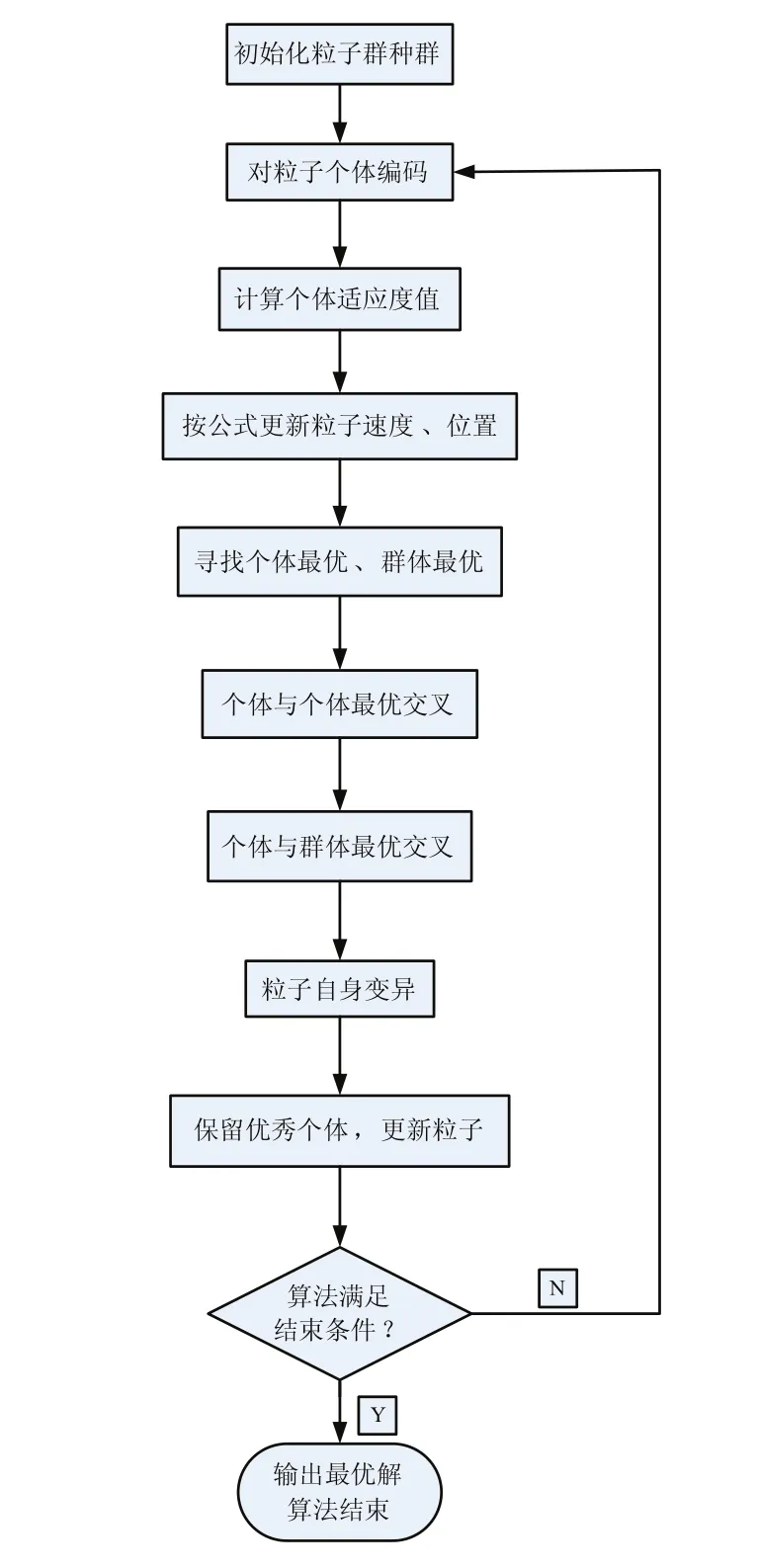
图2 GA-PSO算法螺母紧固优化路径流程图

用GA-PSO算法进行Matlab仿真研究得到仿真结果如图3、图4所示。可寻到的机械手最优运行轨迹如图3所示。迭代过程如图4所示。

图3 GA-PSO算法寻找的机械手最优运行路径

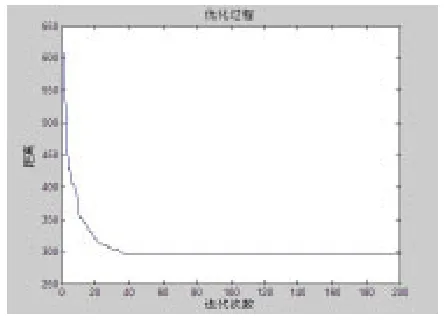
图4 GA-PSO算法的迭代过程

机械手最优运行路径为：

6-1-11-8-12-13-19-10-15-23-21-16-18-20-17-14-22-5-2-4-7-3-9-6

机械手运行最短距离：297.6495(cm)

机械手完成装配最短时间：151.539(s)

4 结果比较与分析

作为对比，本文也采用蚁群算法(Ant Colony Optimization，ACO)对该问题进行研究，与GAPSO进行对比，以验证改进算法的有效性。本文采用的ACO解决紧固螺母路径优化问题的流程图如图5所示。

图5 ACO算法螺母紧固优化路径流程图

ACO可寻优到的机械手最优路径如图6所示。迭代过程如图7所示。

图6 ACO算法寻找的机械手最优运行路径

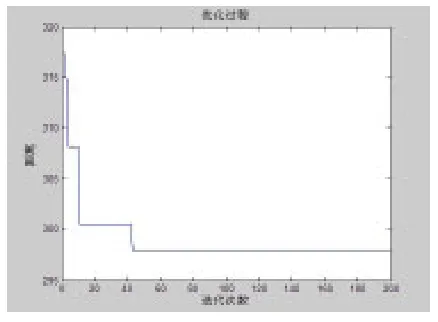
图7 ACO算法的迭代过程

机械手最优运行路径:

5-7-2-4-3-9-6-8-11-1-10-19-12-13-15-23-21-16-18-20-17-14-22-5

机械手运行最短距离: 297.978(cm)

机械手完成装配最短时间：151.5956(s)

5 结束语

本文采用将GA中的交叉和变异操作引入到PSO中得到的改进的粒子群算法GA-PSO对该问题进行研究，通过大量的仿真进行研究，作为对比，本文也采用了ACO对该问题进行研究。仿真结果表明两种算法都能在较短的时间内寻找到最优解，但GA-PSO能够跳出局部极小值(在优化距离上精确了0.3cm左右，在运行时间上精确了0.06s左右)，快速、稳定的寻找到最优路径，验证了改进算法的有效性。而且，ACO中所要设置的参数较多且参数的设置值对算法性能的影响很大。

改进的粒子群算法GA-PSO通过在浙江宁波某汽车配件厂流水线上的使用，有效地求解出机械手的最短路径，缩短机械手工位的作业时间，提高生产节拍，大大提高流水线的生产效率，从而节约成本，提高企业竞争力，使生产效益最大化。

[1] 史峰,王辉,郁磊,胡斐.MATLAB智能算法30个案例分析[M].北京:北京航空航天大学出版社,2011.

[2] 田贵超,黎明,韦雪洁.旅行商问题(TSP)的几种求解方法[J].计算机仿真.2006,23(08):153-157.

[3] 刘青凤,李敏.基于遗传算法的TSP问题优化求解[J].计算机与现代化,2008(02):43-45.

[4] 冯剑,岳琪.模拟退火算法求解TSP问题[J].森林工程,2008,24(1):94-96.

[5] 高海昌,冯博琴,朱利.智能优化算法求解TSP问题[J].控制与决策.2006,21(03):241-247.

[6] 胡中功,李静.群智能算法的研究进展[J].自动化技术与应用.2008,27(2):13-15.

[7] 刘波.粒子群优化算法及其工程应用[M].北京:电子工业出版社.2010.

[8] 杨维,李歧强.粒子群优化算法综述[J].中国工程科学.2004,6(5):87-94.

[9] 纪震,廖惠连,吴青华.粒子群算法及应用[M].北京:科学出版社.2009.1:第1版。

[10] Lv Zhensu,Hou Zhirong.Particle Swarm Optimization with Adaptive Mutation[J].Acta Electronica Sinica,2004,32(3):416-420.

[11] 邓先习.遗传算法求解TSP问题的研究与改进[D].沈阳:东北大学,2008.6.