Kerr介质对二项式光场和三能级原子场熵的影响

田小丽，王建荣

(太原科技大学应用科学学院，太原 030024)

自量子光学理论诞生以来，光与物质之间的相互作用已被人们关注多年，成为量子光学领域研究的热门课题。量子纠缠的概念提出后[1]，人们用量子纠缠研究了光场和原子相互作用的动力学特性，二项式光场的产生[2-3]，二项式光场与级联二能级原子的量子纠缠，及单模多模光场和二能级原子的互相作用等。近来发现，在量子信息表示方面，三能级系统比二能级系统表现出更多突出优点，所以人们对三能级或多能级系统的研究日益广泛，有人研究了二项式光场与级联三能级原子的量子纠缠性质[4-5];研究原子间的失谐量在光场与原子相互作用系统中影响[6];研究Kerr介质的非线性系数在光场与原子相互作用系统中影响[7]，但都没有考虑Kerr介质的非线性系数和原子间的失谐量在光场与原子相互作用系统中的影响。本文利用全量子理论讨论了非线性系数和原子间的失谐量对二项式光场与级联型三能级原子相互作用过程中场熵的影响。

1 二项式光场

单模二项式光场定义为[2]:

其中，M表示最大光子数;η为光场强度参量，当η=0，1时，|ηM〉分别约化为真空态|0〉和Fock态;当 η →0，M→ ∞ 但 ηM= α2= 常数，则|ηM〉约化为相干态。因此二项式态是介于相干态和Fock态之间的一种量子中间态，研究二项式光场和原子的相互作用具有理论及应用价值。

2 理论模型

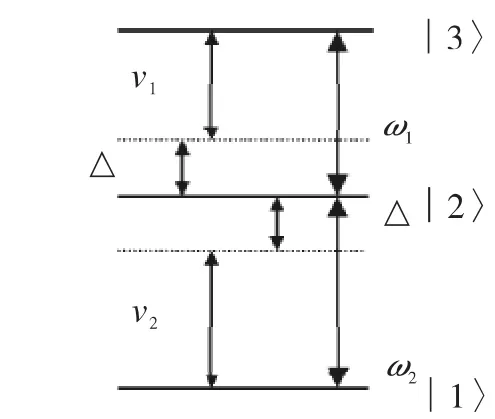
图1 与二项式光场相互作用的三能级原子图Fig.1 Cascade three-atom interaction energy-level diagram with binomial light field

如图1所示的级联型三能级原子模型，|3〉为最高激发态，|2〉为激发态，|1〉为原子的基态。原子在能级|3〉与|2〉，|2〉与|1〉之间跃迁，能级|3〉与|1〉之间为禁戒跃迁。在旋波近似及相互作用绘景中，二项式光场与原子相互作用的哈密顿量为:

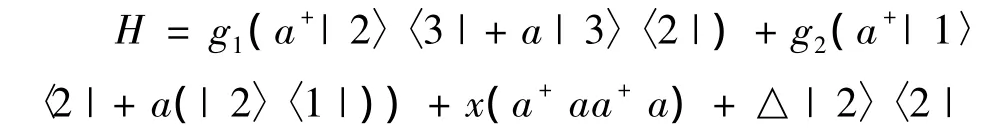
其中a+和a为光场的产生和湮灭算符，g1和g2为原子与光场的耦合系数，本文取g1=g2=g，x为表示介质的三阶非线性电极化现象强弱程度的参量，△ =ω2－v2=ω1－v1为光场与原子耦合的失谐量。

设原子初态处在三个能级的叠加态:

光场处于二项式态，则系统量子态的时间演化可表示为:

两体纯态纠缠度(部分熵纠缠度)为[8-10]:

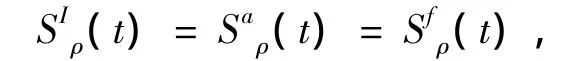
而SIρ(t)的定义为:

其中:ρa(t)=Trf(|ΨI(t)〉〈ΨI(t)|)，

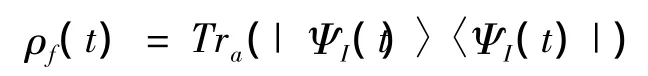
可以证明，纠缠度在0和1.1之间，表征系统局域的混乱程度，量子态的纠缠度越大，从局部上看“局部态”的“不确定程度”就越大。

利用式(3)可得原子和二项式光场相互作用的约化密度矩阵:

二项式光场的约化密度矩阵的本征值λf(t)满足:

方程中系数 u、v、u、w 满足:

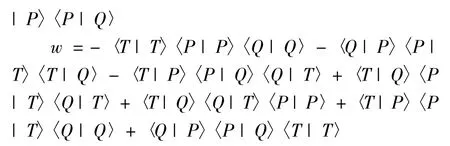
因此，光场和级联三能级原子的量子约化熵可表示为:

3 数值计算及结果分析

取二项式光场的最大光子数M=200，当光场强度η、Kerr介质参数x、失谐量△取不同值，对原子处于不同初始状态时对(5)式进行数值分析计算，可得到场熵随时间的演化特性。场熵的时间演化可以反映光场与原子关联程度的演化特性，熵越高，关联越强，纠缠度越大。在场熵演化曲线中，gt表示时间因子，sf(t)表示场熵值。

3.1 原子的初始状态处于非相干迭加态

原子处于激发态时，取A=0，B=1，C=0数值计算结果如图2，图3所示。

图2 η=0.09 x=0.13时失谐量对场熵演化的影响Fig.2 Entropy evolution of the field with the frequency detuning when η =0.09 x=0.13

由图2可知，在光场强度较小和失谐量为零时，x=0.13时原子间纠缠强烈，周期方面:前期熵值的振荡幅度较大，但随时间的延长，平均熵值趋于平缓且维持较大值。在此过程中增加失谐量的值，即考虑到非共振因素。从图中我们可以看到，体系的熵场值整体下移，即纠缠强度减弱。但会在较短时间内达到稳定。

由图3可知，在光场较强时，x取0.03时原子间纠缠量会达到最值，但场熵值振荡幅度较大，失谐量值的变化对振幅的影响不大。即在此情况下原子间的纠缠不稳定。

3.2 原子的初始状态处于等权相干迭加态

从图4我们可以看出，在Kerr介质系数取1时，体系熵值基本上都在最大值和光场的强弱无关。失谐量在光场较强时对体系熵值影响不大，对周期也没有较大的影响。但是，在弱光场中如果适当地增大失谐量的值却可以使体系的纠缠量的振荡幅度变小，即原子较好的纠缠在一起。

图4 光场强弱，介质系数和失谐量对场熵的影响Fig.4 Entropy evolution of the field with parameters of coherent light field，kerr coefficient and frequency detuning

4 结论

本文从理论上数值分析了二项式光场中Kerr介质系数和失谐量对级联三能级原子纠缠量的影响，得出:当原子处在非相干迭加态时，二项式光场的强弱、Kerr介质系数和失谐量对体系的熵值影响不同。当光场较弱时，能得到稳定的纠缠态，此时Kerr介质的系数决定了纠缠量的最值，且失谐量的大小对纠缠量的幅值有影响;当光场较强时，得不到稳定的纠缠态，此时Kerr介质的系数的影响同上，而失谐量对周期和幅值均没有影响。若原子处在等权迭加态时，当光场较弱时，Kerr介质的系数影响场熵的最大值，且失谐量影响振荡幅值;当光场较强时，Kerr介质的系数的影响同上，而失谐量对体系的熵值没有太大影响。选择合适的Kerr介质的系数和失谐量的值可以得到稳定的纠缠态，这对量子纠缠态的制备有一定的参考价值。

[1]EINSTEIN A，PODOLSKY B，ROSEN N.Can Quantum-Mechanical Description of Physical Reality be Considered Complete[J].Phys Rev，1935，71:777-780.

[2]STOLER D，SALEH B E A，TEICH M C.Binomial states of the quantized radiation field[J].Opt Acta，1985，32:345.

[3]DATTOLI G，GALLARRDO J.Binomiel state of the quantized radiation field:comment[J].Opt Soc Am B，1987(4):185-191.

[4]胡要花，方卯发，廖湘萍，等，二项式光场与级联三能级原子的量子纠缠[J].物理学报，2006，55:4631-4637

[5]李小平，聂义友，胡菊菊.二项式光场与级联型三能级原子相互作用的场嫡演化特性[J].量子电子学报，2005，22:217-221

[6]田永红，彭金生.失谐量对双模真空场作用下级联型三能级原子中光场性质的影响[J].量子电子学报，1999，16(5):29-37.

[7]王建荣，李坤，赖云忠.Kerr介质对真空场级联三能级原子纠缠量的影响[J].太原科技大学学报，2010，31(5):417-419.

[8]SINGH S.Field statistics in some generalized Jaynes-Cummings models[J].Phys Rev A，1982，25:3206-3216.

[9]BARNETT S M，PHONIX S J D.Entropy as measure of quantum optical correlation[J].Phys Rev A，1989 ，40(5):2404-2409.

[10]曾谨言.量子力学新进展[M].北京:清华大学出版社，2003.