杭州湾台风风暴潮增水过程的数值分析*

韩树宗，潘 嵩

（中国海洋大学海洋环境学院，山东 青岛266100）

杭州湾地区地势低平、河网密布，喇叭口的岸线利于能量的汇聚，易受到风暴潮灾害的侵袭。该地区的风暴潮类型主要是台风风暴潮，近些年来，全球气候变暖导致袭击杭州湾地区的台风在频次和影响程度上都有所增加［1］。因此，利用数值模式进行杭州湾风暴潮增水的研究，对于风暴潮灾害的预报和防御具有重要的现实意义。尹庆江［2］利用二维数值模式研究了不同角度登陆的台风和平行海岸移动的台风引起的杭州湾风暴潮，并计算了杭州湾最大可能增水；黄世昌等［3］基于河口海岸二维水动力模式，研究了浙江沿海超强台风在不同登陆地点登陆并遭遇大潮时可能出现的风暴潮增水过程和最大增水。以上研究均采用二维数值模型和矩形网格。本文利用FVCOM三维近海海洋数值模式，采用对岸线拟合效果更好的三角网格，建立了杭州湾风暴增水数值模型，研究和分析了移动速度、移动路径、最大风速半径等不同台风要素对杭州湾地区风暴潮增水的影响。

1 模式介绍

FVCOM是由美国马萨诸塞州立大学开发，基于无结构三角网格，采用有限体积法求解原始方程组的三维近岸海洋数值模式。该模式将有限元方法拟合岸线较好和有限差分简单高效的优点结合在一起，通过积分计算三角形控制体的通量的方式来求解控制方程，保证了质量、动量和能量的守恒［4］，诸多研究者利用该模式研究了中国近海的潮汐潮流及风暴潮［5－6］。

2 模型设置及验证

2.1 模型设置

模型计算区域为117.2°E～128.0°E，22.8°N～41.0°N。水平方向采用可变分辨率网格，在关注区域对网格进行局部加密，杭州湾地区最高分辨率可达500m。整个计算区域内共有18 990个网格节点和36 023个三角单元，垂直方向分为10层，采用σ坐标系，计算网格见图1。

本模型所用海岸线数据来自美国地球物理数据中心的高精度岸线数据，下载地址为http：／／www.ngdc.noaa.gov／mgg／shorelines／shorelines.html，水深由美国国家地学测量中心出版的变分辨率全球水深数据（http：／／www.ngdc.noaa.gov／mgg／global／global.html）线性内插得到。杭州湾地区的岸线和水深，根据中华人民共和国海军航保部出版的最新版海图进行订正。杭州湾地区的水深地形如图2所示。

本模型初始流速场与水位场均设为零值［7］。天文潮计算中，模型由开边界给定的潮位进行驱动，开边界考虑八大主要分潮：M2、S2、K1、O1、N2、P1、Q1，K2，由T－TIDE MATLAB工具包预报生成开边界水位［8］。计算时间为1997年7月31日～8月31日。长江径流量取洪季平均下泄量40 000m3／s。钱塘江属于山溪性河流，水位和流量的变率较大，但与长江相比径流量要小得多，因此本模型不予考虑［9］。根据CFL条件及多次试验的效果，内模时间步长确定为2s，外模时间步长与内模的比值为10，迭代稳定时间为72h。

图1 计算网格图Fig.1 Calculation mesh of the model

图2 杭州湾附近水深地形图Fig.2 Topography of the Hangzhou Bay

2.2 天文潮模拟验证

本文选取了2个位于杭州湾内的验潮站：大戟山和滩浒的潮汐调和常数资料，验潮站的位置见图2，根据调和常数计算出1997年8月1日00时～15日00时的潮位作为“实测值”，与模型模拟结果进行对比验证，结果见图3，蓝色实线为模拟值，红色点线为实测值。从图中可以看出模拟潮位与实测潮位符合较好，变化趋势较为一致。

2.3 风暴潮模拟验证

本文选取了曾对杭州湾地区产生较大影响的9711号台风，它于1997年8月10日在15.4°N，153.8°E的西北太平洋洋面生成，此后以18km／h的速度稳定地向西北偏西方向移动，过程中逐渐加强为中心气压为920hPa，最大风速为60m／s的强台风。18日21∶32在浙江省温岭市登陆时，近中心最大风速为40m／s。台风登陆后以25km／h的速度经浙江进入安徽逐渐转向偏北方向移动，移动速度明显加快，并减弱为热带风暴［10］。

本文采用Jelesnianski圆形风场模型［11］计算得到驱动模型的风场和气压场，其余模型设置均与天文潮模拟相同。

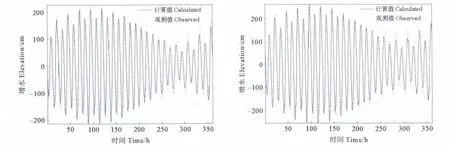
图3 实测潮位与模拟潮位的比较Fig.3 Comparison of the tidal level between observation data and calculation results

验证资料取自大戢山、滩浒在台风期间的余水位数据。计算时间自1997年08月15日00时开始，模拟144h。将模拟水位减去潮汐预报水位得到增水值，与2个验潮站余水位数据进行对比验证，对比结果见图4。图中虚线表示实测值，实线表示模拟值。实测数据显示，9711号台风期间，杭州湾内出现明显的增水过程，大戟山站最大增水为108cm，而滩浒站由于比大戟山更靠近湾顶，最大增水值更大，为176cm。2站最大增水发生时刻均在台风登陆时刻附近，滩浒站要比大戟山站晚1h。对比结果显示，模拟结果基本再现了台风期间两站的水位变化过程，大戟山站模拟最大增水值为102cm，滩浒站模拟最大增水值为206cm，但台风过境后的水位模拟情况较差，误差产生的原因可能是本模型中也没有考虑波浪的作用。有研究表明，波浪能够显著影响表面风应力，进而影响风暴增水。个例研究表明，最大量级可达1.3m。如果在模型中考虑波浪的作用，可以改善模拟效果［12］。

图4 风暴潮增水模拟结果与实测资料的比较Fig.4 Comparison of the storm surge between the calculation results and observed data

3 敏感性实验

敏感性实验中作为对照组的标准台风各要素为：移动路径为西北向，中心移动速度5m／s，中心气压950hPa，最大风速半径50km，最大风速38.0m／s［13］，登陆地点为舟山，台风中心匀速移动，计算起止时间为登陆时刻前后36h。本文在长江口及杭州湾地区选取了5个具有代表性的站点（以字母A、B、C、D、E表示，站点位置见图2），研究其水位变化情况。

3.1 移动速度对杭州湾风暴潮增水的影响

本文将标准台风的移动速度分别扩大和缩小1倍，即取10和2.5m／s，通过对比其各自造成的增水情况，研究移动速度对杭州湾风暴潮增水的影响。

A、B、C、D、E 5个站点的水位变化曲线见图5。从各站水位变化曲线中能够得出：增水极值仍然发生在各自台风登陆时刻附近，分别为自计算开始时刻起18，36和72h。各站的增水极值均随着台风移速度的增加而减小，除B站外，其他各站最大值与最小值的比值均在2.6左右。

杭州湾内的水体分布在风应力的作用下发生变化，以产生水位梯度来平衡风应力，此过程并不是瞬时完成的，因此风应力的作用时间对于水位变化过程的重要性就凸显出来。冯士筰［14］曾对狭长海区的风暴潮成长过程进行过探讨，海面风应力建立了风生流，其流量的顺风运移形成了风暴潮的水位梯度，从而产生反向的流动，它抑制了正向流的发展，直至全流消失的定常状态，这个过程的时间尺度可表示为T＝L2β／πgh，L为海湾的长度；β为1个与湍阻尼系数有关的量；g为重力加速度；h为水域的平均深度。其中β的表达式为，β正比于湍黏性系数，反比于水深的平方。冯士筰［14］指出在渤海，可以取特征值h＝20m，β＝10－4s－1。对于杭州湾来说，L＝120km，h＝7.5m，则β＝7×10－4s－1，T的估计值为12h。对于实验中移动速度分别为10、5和2.5m／s的3个台风，经过杭州湾所需要的时间大致分别为3，6和12h。这就是说移动速度较快的台风（移动速度10m／s）没有足够的作用时间建立水位梯度，而移动速度较慢的台风（移动速度2.5m／s）则能够影响该地区更长时间，使得增水能够充分发展，因此移动速度快的台风造成的增水极值也相对较小。

图5 不同移动速度各站点水位变化曲线Fig.5 Time series of surge of the nodes concerned for different approaching speed

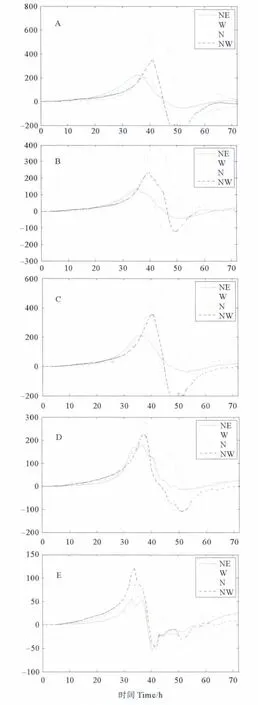
图6 不同移动方向各站点水位变化曲线Fig.6 Time series of surge of the nodes concerned for different driection

3.2 移动路径对杭州湾风暴潮增水的影响

本文根据日本气象厅（JMA）发布的台风最佳路径数据，统计出1995—2010年间影响长江口及杭州湾地区16个台风，各台风的路径见图7。根据图示，影响该地区的台风路径可大致分为3种：东北向、北向、西北向。直接登陆杭州湾附近地区的台风较少，仅有9806号台风一例，登陆地点位于舟山群岛。

图7 1995—2010年间影响杭州湾地区的台风路径Fig.7 Tracks of the typhoons that has attacked the region of the Hangzhou Bay

结合前人［15－16］和本文关于影响杭州湾地区的台风特征和分类的统计结果，本文在敏感性实验中，移动路径分别取西（NE）、西北（NW）、北（N）和东北（NE），来探讨台风移动路径变化对杭州湾增水的影响，各站点的水位变化曲线如图5所示。

计算结果表明，对位于杭州湾内的各站点（A、B、C、D）来说，增水极值最大的台风均为即垂直湾口两端连线向西移动的台风，这与尹庆江［2］、王喜年［17］的计算结果是一致的。除E站外，其余4站均位于湾内，其水位变化呈现出较为一致的趋势。

而位于湾外浙北舟山群岛附近的E站点，则是东北向移动的台风造成的增水极值较大，这与杭州湾内的4个站点并不相同。羊天柱等［18］曾对浙江海岛台风风暴潮增水特点做了统计分析，结果表明，位于浙北岛区的海岛，N～NE风向为增水风向，即吹N～NE风时台风增水逐时增加，增加幅度随着风速的增强而上涨，而趋于偏W风场时，增水急剧下降，岛区甚至可出现减水。E站同属浙北岛区，在不同路径的台风作用下的风速风向变化结果见图7。结合图8的E点水位变化曲线，E点在W、N、NW向移动的台风作用下的增水过程中，风向均为N～NE向，且风速量值从大到小依次为NW、W、N，与水位变化曲线呈现良好的相关性，这与羊天柱等人的统计结论是一致的。

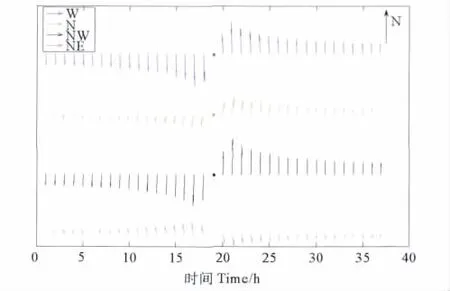
图8 不同台风移动方向E站风矢量图Fig.8 Wind speed and direction of E for different direction

3.3 最大风速半径对杭州湾风暴潮增水的影响

各站点的增水极值随最大风速半径Rmax变化的结果见图9。整体来看，各点的增水极值随最大风速半径的增大而增大，这是由于最大风速半径增大会导致局部风速增大。越靠近湾顶的站点，对最大风速半径的变化越敏感，增加的趋势越明显。随着最大风速半径由45km增加到125km，A点的增水极值由3.5m增加到5.4m，增幅高达1.9m；而B点的增水极值由2.3m增加到3.2m，增幅仅为0.9m。但是这种增大的趋势并不是无限制的，随着最大风速半径的增大，曲线的斜率在变小，即增大的趋势在放缓，这是由于在移动速度不变的前提下，最大风速半径增大在导致局地风速增大的同时，同样会导致大风作用时间的缩短，通过3.1的分析得知，台风的作用时间越短会抑制增水幅度的增大。

图9 不同最大风速半径各站点增水极值Fig.9 Maximum surge at A～E spots for different maximum wind speed radius

4 结语

本文使用Jelesnianski圆形风场和FVCOM三维近海海洋模式，建立了杭州湾地区风暴潮数学模型，模拟了9711号台风风暴潮增水并与实测余水位数据对比。结果显示，模拟结果良好。通过单变量敏感性实验，研究了不同台风要素：移动速度、移动路径和最大风速半径对杭州湾地区台风风暴潮增水的影响。结果表明：台风的移动速度对风暴潮增水的影响是明显的，移动速度较快的台风没有足够的作用时间建立水位梯度，而移动速度较慢的台风则能够影响该地区更长时间，因此移动速度快的台风造成的增水极值也相对较小。垂直杭州湾湾口连线向西移动的台风对湾内各点造成的增水最大，对于位于浙北的杭州湾湾外的浙北岛区，则向东北移动的台风造成的增水极值较大。台风的最大风速半径对风暴潮增水也有不可忽略的影响，各点的增水极值随最大风速半径的增大而增大，但是这种增大的趋势并不是无限制的，随着最大风速半径的增大，增大的趋势在变缓。

［1］ 杨桂山.中国沿海风暴潮灾害的历史变化及未来趋向［J］.自然灾害学报，2000，9（3）：23－30.

［2］ 尹庆江.杭州湾可能最大台风风暴潮计算［J］.海洋预报，1991，8（4）：41－49.

［3］ 黄世昌，李玉成，赵鑫，等.浙江沿海超强台风作用下风暴潮增水数值分析［J］.海洋工程，2008，26（3）：58－64.

［4］ Chen C S，Liu H D，Beardsley R C.An unstructured，finite－volume，three－dimensional，primitive equation ocean model：Applica－tion to coastal ocean and estuaries［J］.Journal of Atmospheric and Oceanic Technology，2003，20：159－186.

［5］ 冯兴如，杨德周，尹宝树.FVCOM在龙口海域潮汐潮流模拟中的应用研究［J］.海洋预报，2010，34（6）：94－99.

［6］ 耿姗姗.长江口杭州湾海洋动力要素对风场响应的FVCOM模拟研究［D］.南京：南京信息工程大学，2011.

［7］ Chen Xueen，Zhang Peng，Chen Jinrui，et al.Numerical study of current fields near the Changjiang［J］.Acta Oceanol Sin，2011，30（5）：33－44.

［8］ Pawlowiczr R P，Beardsleyb B B，Lentzs S L.Classical tide harmonic analysis including estimation MATLAB using T－TIDE［J］.Computers and Geosciences，2002，28：929－937.

［9］ 黄华.长江口及杭州湾风暴潮三维数值模拟［D］.上海：华东师范大学，2005.

［10］ 韩树宗，郑运霞，高志刚.9711号台风对日照近海悬沙浓度影响的数值模拟［J］.中国海洋大学学报：自然科学版，2008，38（6）：868－874.

［11］ Jelesnianski C P.A numerical computation of storm tides induced by a tropical storm impinging on a continental shelf［J］.Mon Wea Rev，1965，93（16）：343－358.

［12］ 尹宝树，王涛，侯一筠，等.渤海波浪和潮汐风暴潮相互作用对波浪影响的数值研究［J］.海洋与湖沼，2001，32（1）：109－106.

［13］ Typhoon Committee.Operational Manual［M］.［s.l.］：World Meteorological Organization，2011.

［14］ 冯士筰.风暴潮导论［M］.北京：科学出版社，1982.

［15］ 丁骏，车助美.浙江沿海台风风暴潮类型与成因初探［J］.海洋预报，2003，20（2）：5－14.

［16］ 贾晓，路川藤，卢坚，等.中国沿海台风的统计特征及台风浪的数值模拟［J］.水道港口，2010，31（5）：433－436.

［17］ 王喜年.SPLASH模式诺模图方法在我国的应用［J］.海洋通报，1983，2（4）：26－31.

［18］ 羊天柱，应仁方.浙江海岛风暴潮研究［J］.海洋预报，1997，14

（2）：28－43.