非静压海洋数值模式加速计算的CUDA实现*

王春晖，苗春葆，沈 飙**

（1.中国海洋大学物理海洋实验室，山东 青岛266100；2.国家海洋局北海环境监测中心海洋溢油监别与损害评估技术重点实验室，山东 青岛266033）

自从NVIDIA提出CUDA框架以后，使用GPU进行通用计算变得相当简单［1］。CUDA以扩展的C语言为基础，取代了以前基于GPU的程序设计模式，采用CUDA技术，程序员不需要将计算转化成图形函数，提高了程序开发的灵活性［2］。在CUDA编程模型中，GPU被视为1个协处理器，通过大量线程的并行执行来加快计算速度。在CUDA架构下，1个程序分为两部分：主机（Host）端和设备（Device）端。主机端是指在CPU上执行的部分，而设备端是在GPU上执行的部分，在GPU端执行的程序称为“核”（Kernel）。CUDA程序执行时，驱动程序会将GPU端代码编译成可执行程序，并传送到GPU运行。在GPU上会产生大量的线程，每一个线程都会去执行核程序，虽然程序有同一份，但由于每个线程的索引值不同，因而各个线程就能对不同的数据进行计算［3］。

在自然界发生的很多流体运动中，表面水波是最容易被观察到的，由于地球表面大约三分之二的面积被水覆盖，因此对水波的研究就具有重要的实际意义。对浅水波进行数值模拟时，若垂向压力一直满足静压假设，则Navier－Stokes方程可以得到简化，不用求解泊松方程。但在自由表面有较大变化、地形突变、或垂向掺混比较严重的区域，采用这种假设的模拟结果会有很大误差；若使用非静压模式进行模拟，计算量会有明显的增加，难以在较短的时间内完成计算任务。因此，本项目使用CUDA实现对表面水波数值模拟的GPU加速，实现非静压表面水波的较快的数值模拟。

与CPU串行程序相比，可以在不牺牲模拟精度的前提下（相对误差不超过2×10－3）大大提高计算效率；计算速度的显著提高展现了海洋数值模式应用GPU进行加速的广阔前景。

1 数值模型

1.1 基本方程

流体作为物质的一种形态，遵循自然界中关于物质运动的普遍规律，例如质量守恒、动量守恒和能量守恒等。为简单起见，本项目采用描述海水运动的二维垂向切片模型［4］，其控制方程为：

其中：u代表水平方向的流速；w代表垂向流速；ρo代表海水密度；P代表压强；η表示海面水位起伏。

1.2 差分格式

参 考 Jochen Kampf［4］， 对 上 述 控 制 方 程 在Arakawa C网格上进行差分计算（见图1），垂向采用z坐标。

动压强P可以分为两部分：

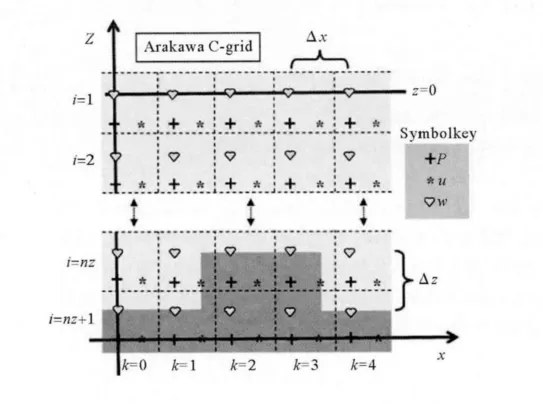
图1 Arakawa C网格中各变量位置分布Fig.1 Arakawa C－grid for a vertical ocean slice

其中：p代表平静海平面的静压强；q由两部分组成，一部分是海平面倾斜造成的压强变化，第二部分是非静压效应造成的压强变化。若海水密度是一个常量，方程（5）可以简写为：P＝q。把q分解为当前时刻n的压强加上下一时刻n＋1的变化值，即：

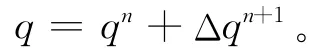
相应的，方程（1）～（4）的求解过程可以分为2步：第一步，在时刻n显式求出初始猜测流速u＊跟w＊；第二步，隐式求出Δq。

流速的初始猜测值可以由时间前差方案获得，即：

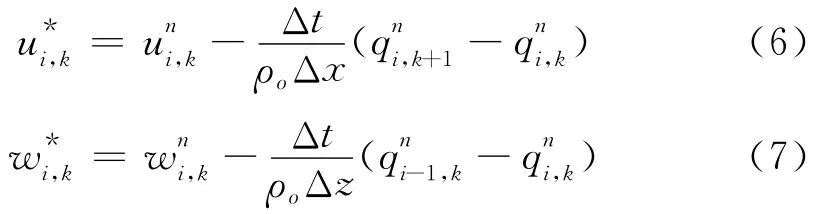
其中：i跟k分别代表网格的水平和垂向索引。动量方程的有限差分格式为：

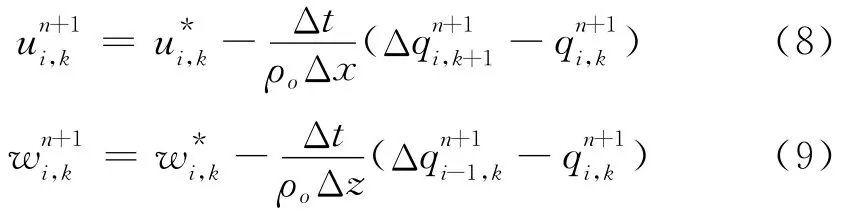
将方程（8）、（9）代入方程（3），两边同时乘以ΔzΔx，可以得到：

该方程在数学上被称为泊松方程，其中：

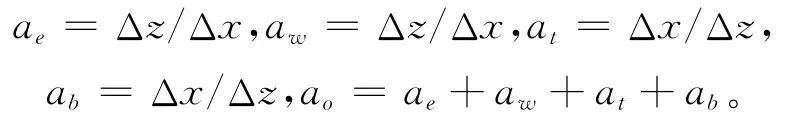
图2给出了这些系数在Arakawa－C网格中的位置关系。方程右边包含了初始猜测流速场（u＊，w＊）的散度，即：

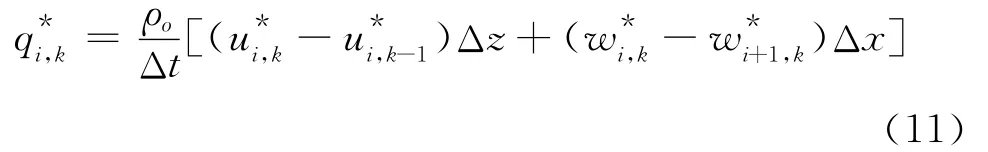
方程（10）的解意味着流场没有散度，即满足流场的不可压缩条件，新的压强场则可以表示为：

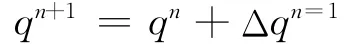
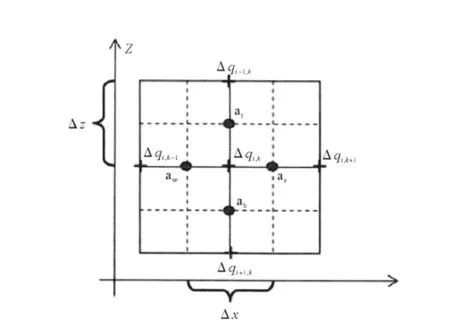
图2 ae，aw，at，ab 的位置关系图Fig.2 Location used to define the coefficients ae，aw ，atand ab.

1.3 泊松方程的求解算法

方程（10）可以采用高斯 －赛德尔迭代（Gauss－Seidel，简称 G－S方法）或超松弛迭代法（Successive Over－Relaxation，简称SOR方法）进行求解［4］。用方程表示如下：

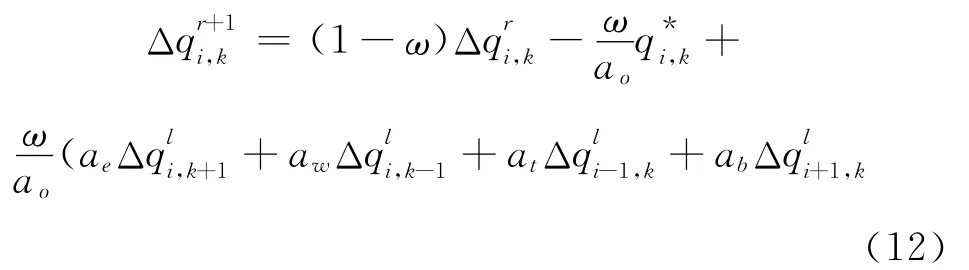
其中：r＝0，1，2，…代表迭代次数；上标l由Δq是否更新决定，即l＝r＋1或l＝r；ω的取值与采用哪种方法有关：若采用G－S方法，则ω取值为1，若采用SOR方法，则ω的典型取值范围为1.2～1.4。SOR方法与G－S方法相比其优势在于：通过选择松弛因子ω，可以使得迭代过程收敛较快。

G－S方法及SOR方法中Δq的初始值可以设置为0，但是如果初始值采取前一步的取值，会使计算迭代次数明显减少，提高计算效率。即：

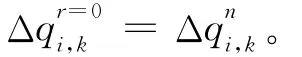
海表面压力在每次进行迭代时都需要进行计算。具体计算过程如下所

（1）对流速进行更新

（2）在垂向上积分水平流速

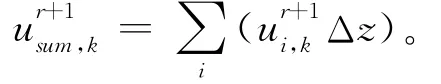
（3）忽略海平面变化引起的水体厚度的轻微变化，海表压强的变化可用下面公式表示：

重复G－S方法或SOR方法，直到相邻2次迭代的差满足要求，即：

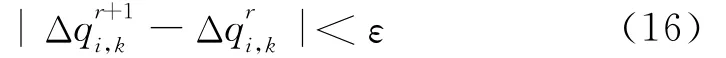
其中：ε是2次迭代之间压强的允许误差。根据方程（11）可知，此时意味着：

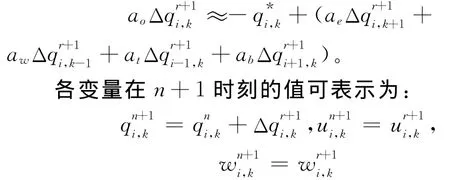
其中：上标为r＋1的值即为G－S方法或SOR方法的解。图3给出了G－S／SOR方法计算流程图。虽然SOR方法收敛速度更快，但其各个网格的计算具有严格的顺序性，无法实现并行计算，因此这里采用G－S算法对方程（10）进行求解。

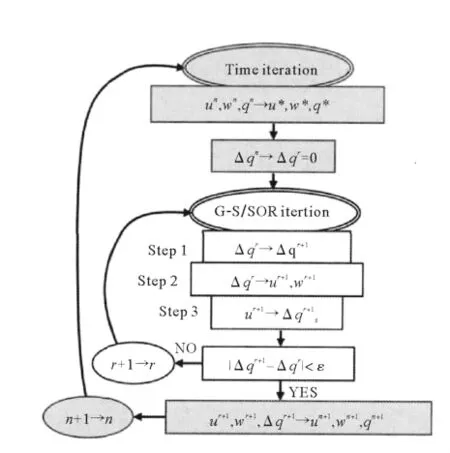
图3 G－S／SOR方法计算流程图Fig.3 Flow chart of the G－S／SOR method

1.4 串行程序的实现

用C语言实现以上求解算法，计算流程图如下：

计算过程中所用到的主要函数及其功能为：

（1）init函数：初始化变量的值，为变量赋初值；

（2）dyn函数：动力过程的计算，计算下一个时间步各变量的值；

（3）store＿surf＿dp函数：将海表面压强变化保存到另一个数组；

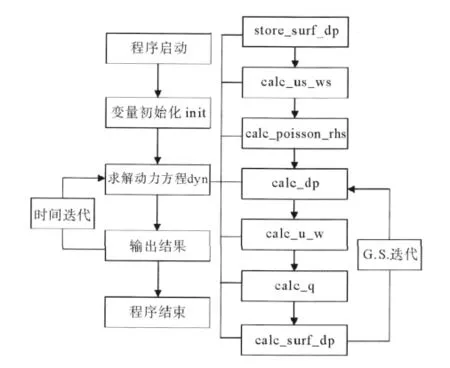
图4 C语言程序计算流程图Fig.4 Flow chart of the C language procedure code

2 基于CUDA的并行程序的实现与优化

通过对各子程序进行并发性（concurrency）分析可知，每个子程序均可以采用并行算法进行计算加速，但由于init函数计算量较小，且仅调用一次，因此不需要采用GPU进行加速；但对于动力方程计算dyn的7个函数，计算量均较大，因而可以将这些程序改为kernel函数，用GPU进行计算。程序的优化可以分为以下5个部分：

2.1 全局存储访问的程序优化

全局存储器（global memory）即普通的显存，GPU与CPU都可以进行读写访问，网格中的任意线程都可以对全局存储器的任意位置进行读写。全局存储器具有较高的访问延迟，比较容易成为性能瓶颈［3］。能否满足合并访问在很多情况下会使CUDA程序的速度产生高达一个数量级的差异。CUDA中实际执行单元是以warp为单位的，在Fermi架构中，1个warp由32个线程组成，每次GPU调度1个warp里的32个线程执行同一命令，同在1个warp的线程以不同数据资源执行相同的指令。如果同一个warp中的线程对全局存储的访问满足合并访问条件，则可以达到对存储带宽的完全充分利用［5］。

C语言的二维数组是行序存放的，使用CUDA访问global memory时，要使访问效率最高，应该从256字节对齐的地址（即addr＝0，256，512…）开始进行连续访问，因此，为提高内存访问的效率，有2种方法：第1种是使用cudaMallocPitch函数进行自动对齐，该函数分配的内存中，数组每一行中第1个元素开始的地址都保证是对齐的。由于每行有多少个数据并不确定，即每行的元素不一定是256的倍数，因此，为了保证数组每一行中第1个元素开始的地址是对齐的，cudaMallocPitch函数在分配内存时，每行都会多分配出一些字节，从而保证每行中的元素加上多分配的字节恰好是256的倍数（对齐）；第2种方法是手动对齐，即定义数组时保证是数组第二维是256的倍数，在本项目中作者采用第二种方法，保证数组的第二维，即nx＋2为256的倍数，此时有效带宽达到最大。

2.2 使用共享存储器进行程序优化

共享存储器（shared memory）位于GPU片内，是一块可读写高速存储器，能被同一block中的所有线程访问。对共享存储器变量的声明通过＿＿shared＿＿来实现。在并行访问时为了能够获得高带宽，其被划分为能被同时访问且大小相等的存储器模块（bank）。不同的bank可以互不干扰的同时进行工作，因此可以同时访问位于n个bank上的n个地址，有效带宽为仅有一个bank时的n倍。但假如warp请求访问的很多个地址位于同一个bank中，此时bank在1个时刻不能响应多个请求，因此这些请求就必须被串行地完成，即出现存储器冲突，这时硬件会将造成存储器冲突的访存请求进行划分，分成几次不存在冲突的独立请求，同时有效带宽会降低数倍，降低的倍数即拆分后得到的不存在冲突情况的请求个数请求［6］。

计算核函数void calc＿dp和calc＿u＿w时多次用到Δq，因此可以在程序中将数组Δq加载到共享存储器，提高有效带宽，但由于程序中用到的频率并不是太高，有效带宽提高不大，计算时间只是略有减少。

2.3 使用常数存储器进行程序优化

常数存储器（constant memory）是只读的地址空间，其数据位于显存，且拥有缓存机制，用以节约带宽，加快访问速度［7］。常数存储器与全局存储器相比，在读取或者存入数据时都具有很小的延迟、很高的速度。声明常数存储器通过＿＿constant＿＿来实现。

在本项目中，除边界处外，方程（11）中的ae，aw，at，ab在大多数网格中都是相同的，因此将其由数组改为常数，然后使用常数存储器进行优化。该方法有效减少了对全局存储的访问，大大提高了计算效率。

2.4 使用多个流进行程序优化

程序管理并发需要通过流（stream）来实现，流是按顺序执行的一系列命令，但不同流之间则没有这一顺序性，在支持多个流并行的设备上是并行执行的。这样，可以使一个流的计算与另一个流的数据传输同时进行，从而提高GPU中资源的利用率。

流的定义方法是创建一个cudaStream＿t对象，并在启动内核和进行memcpy时将该对象作为参数传入，参数相同的属于同一个流，参数不同的属于不同的流。执行参数没有流参数，或使用0作为流参数时，则使用默认的流。当使用默认的流进行任何内核启动、内存设置或拷贝函数时，只有在之前设备上所有的操作均已完成后才会开始。

在本项目中，设置参数isconverge作为判断循环是否终止的条件，若满足方程（16），则isconverge＝1，迭代终止；相反，若不满足方程（16），则isconverge＝0，迭代过程继续。由于每次迭代是否收敛的判断需要在设备端进行，而是否退出整个迭代循环的操作需要在主机端进行，所以在每次迭代时都会把isconverge的值由设备端拷贝到主机端，这会花费一定的时间。而isconverge的拷贝是可以与核函数执行同时进行的，因此，这里创建2个流，将核函数调用放在stream0中，而设备端到主机端的数据拷贝放在stream1中，从而使用计算时间掩盖了主机设备通信时间，显著提高了程序的效率。

2.5 网格及线程块的维度设计

CUDA在执行内核函数时，block会被分配到SM（流多处理器）中执行。对于block的尺寸应该优先考虑，而对于grid的尺寸，应该根据问题的规模予以分配。

block的尺寸与数据划分紧密相关。较小的block使用资源较少，一般在1个SM中能够有更多的active block；而block较大时，意味着可以进行通信的线程更多，此时指令流效率也更高。为了有效利用执行单元，应该让每个block中的线程数量是32的整数倍，且最好为128～256之间，因此在本项目核函数中block的维度，均取为256。

为了提高访问全局存储器和共享存储器的效率，blockDim.x在Telsa架构中应设计为16的整数倍，在Fermi架构中，blockDim.x 应为32的整数倍［8］。在block的尺寸及维度确定以后，就可以按照实际问题的规模对grid中各个维度的block数量进行确定。一般的，grid在某个维度上的block数量为：

grid在某方向的block数量＝（问题在该方向上的尺寸－1）／每个block在该方向的尺寸＋1。

因为整数除法只会取结果的整数部分，这样可能使问题的边界得不到处理，引起错误，因此需要在后面加上1，以保证block数量满足实际要求；若问题在某方向的尺寸恰好为每个block在该方向尺寸的整数倍，此时后面＋1反而会导致block数量多于实际要求的数量，因此需要在前面的括号内减去1。

3 模拟结果及性能分析

3.1 测试平台

进行测试时，所有不必要程序全部关闭，测试的软硬件环境配置如下：

出自《圣经》。上帝对人类所犯下的罪孽非常忧伤，决定用洪水消灭人类。诺亚是个正直的人，上帝吩咐他造船避灾。经过40个昼夜的洪水，除诺亚一家和部分动物外，其他生物都被洪水吞没。

CPU AMD Phenom（tm）II x4 965 内存：4G

GPU NVIDIA Geforce GTX 560Ti 显存：1G

主板 技嘉GA－MA790GP－UD3H

主板芯片组 AMD 790GX

总线接口标准 PCI－Expressx16 2.0

操作系统 Windows HPC Server 2008R2 64位

3.2 模拟结果

模式中水平网格大小为5m，垂向网格大小为2m，时间步长为0.05s。图5为模拟的各时刻的水位起伏，可以看到，随着时间的推移，重力波从左逐渐向右传播，重力波造成的水位起伏在海面处最大，随着深度的增加逐渐减小，到海底处为0。

下面对摸拟结果进行误差分析，保留计算结果中每个时刻、每个网格dp的值，仅对dp不为0的点进行统计误差分析，CUDA程序与CPU串行程序的相对误差计算公式为：

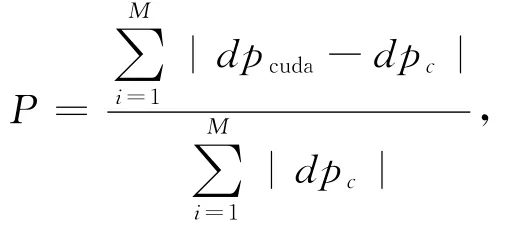
其中：dpcuda代表CUDA程序计算结果；dpc代表CPU串行程序的计算结果；M代表结果不为0的网格点总数。统计结果见表1。由表1可以看出，网格数较小时，CUDA程序与CPU串行程序计算结果的相对误差较小，随着网格数的增大，相对误差也随之增大，并逐渐趋向稳定；不管是采用单精度计算，还是采用双精度计算，相对误差均未超过2×10－3，这说明模拟结果稳定，可靠。

表1 不同网格数CUDA程序模拟误差Table 1 Simulation errors of CUDA code with different grids

3.3 性能分析

C语言的time库函数中包含很多时间函数，其中的clock函数可以对程序运行时间进行检测。为尽可能减小误差，对每个程序运行10次，将平均值作为最终结果。单精度的计算时间对比及加速比见图6和7。

图6 单精度计算时间对比Fig.6 Comparison of computation times of GPU code and CPU code with single precision

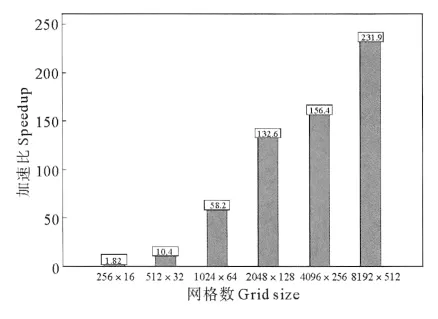
图7 单精度计算加速比Fig.7 Speedup of the GPU code relative to the serial CPU code with single precision

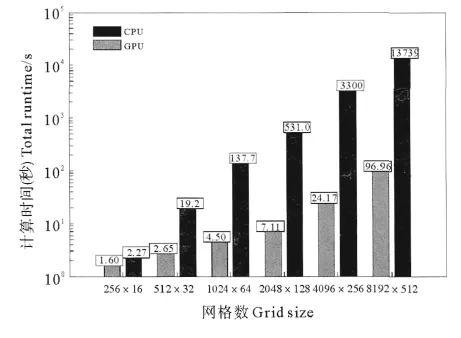
图8 双精度计算时间对比Fig.8 Comparison of computation times of GPU code and CPU code with double precision

由于网格点数较少时计算时间较少，所以将y轴采用对数坐标，从图7中可以看出，当网格点数较少（256×16）时，GPU运行速度与CPU运行速度相当，加速比仅为1.82，这是由于数据传入或传出设备（GPU）、启动kernel等都需要浪费一定的时间，当网格数较少时，这部分所占时间比重较大，因此总的计算时间相差不大；随着网格数的增加，CPU计算时间均急剧上升，而GPU计算时间上升较慢，即此时加速比（CPU计算时间／GPU计算时间）也急剧增大，但当网格数增大到2 048×128以后，加速比增速明显放缓，当网格数为8 192×512时，加速比可以达到231.8倍。这说明问题规模越大，加速比也越大，越适合应用CUDA程序进行GPU并行加速计算，而问题规模较小时，加速比较小，使用CUDA程序进行计算意义不大。

当采用双精度计算时，可以得到与采用单精度计算时大致相同的结论（见图8和9），只是加速比比用单精度计算要小，网格数为8 192×512时的加速比为141.7。可以看出尽管Fermi架构相对Tesla架构双精度浮点处理能力已有很大的提升，但仍有很大的改进余地。

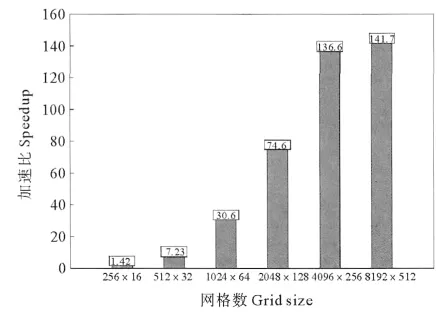
图9 双精度计算加速比Fig.9 Speedup of the GPU code relative to the serial CPU code with double precision

4 结论

自从CUDA在2007年首次出现以来，已在医学图像、视频播放、信号处理、生物计算等领域获得了广泛的应用。这是因为GPU相对CPU拥有更高带宽的独立显存、适合处理并行计算任务且能够大幅降低系统成本，从而为这些问题提供了新的解决方案。

在物理海洋研究中，数值模拟是一个非常重要的研究手段。而高分辨率海洋数值模拟的计算量是很大的，为了尽快取得模拟结果，需要借助高性能计算机来减少程序的运行时间。而CPU的计算能力无法满足海洋数值模拟对计算能力的要求。海洋数值模式具有非常高的计算密度，非常适合使用GPU来进行加速计算，而目前大部分海洋数值模式的计算都基于CPU为核心，还没有移植到GPU平台，因而无法利用GPU强大的计算能力。本项目使用CUDA实现了一个非静压海洋数值模式的GPU加速计算，在海洋数值模式的GPU加速方面进行了初步的尝试。与CPU串行程序相比，基于GPU的程序可以在不牺牲模拟精度的前提下（相对误差不超过2×10－3）大大提高计算效率；单精度计算的加速比最高可以达到232，双精度计算的加速比最高可以达到142。本项目为海洋数值模式向GPU平台的移植积累了丰富的经验，计算速度的显著提高展现了海洋数值模式应用GPU进行加速的广阔前景。

同时值得注意的是，CUDA中GPU的编程模型和CPU有很大的差别。数据的输入输出以及很多初始化工作需要由CPU完成，高密度的计算部分需要在GPU上完成，而CPU和GPU能访问的存储空间是隔离的，这样需要在主机端和设备端进行数据的显式传输，而且主机端代码和设备端代码有明显的区分，因而将传统的大量的海洋数值模式完全移植到GPU平台是非常耗时的。除了直接使用CUDA外，还可以使用OpenACC或者一些GPU函数库来实现GPU上的加速计算，但这些方式是否能够既方便地将海洋数值模式移植到GPU平台，又充分发挥GPU的计算能力，还需要进行实际的使用和检验。

［1］ Folkert B，Rob H B，Henk A D.Accelerating a barotropic ocean model using a GPU［J］.Ocean Modelling，2012，41：16－21.

［2］ 周 洪，樊晓桠，赵丽丽.基于CUDA的稀疏矩阵与矢量乘法的优化［J］.计算机测量与控制，2010，18（8）：1906－1908.

［3］ 张 舒，褚艳利，赵开勇，等.GPU高性能运算之CUDA［M］.北京：中国水利水电出版社，2009：14－81.

［4］ Jochen K.Advanced Ocean Modelling：Using Open－Source Software［M］.Berlin：Germany Springer，2010：21－35.

［5］ CUDA C Best Practices Guide Version 4.1［EB／OL］.［2012－01－11］，［2012－12－03］.http：／／nvidia.com.

［6］ NVIDIA CUDA C Programming Guide Version 4.2［EB／OL］.［2012－04－16］，［2012－12－03］.http：／／nvidia.com.

［7］ Jason S，Edward K.CUDA by Example：An Introduction to General－Purpose GPU Programming［M］.USA：Addison－Wesley，2010：37－57.

［8］ Tuning CUDA Applications for Fermi Version 1.5［EB／OL］.［2011－05－03］，［2012－12－03］.http：／／nvidia.com.