典型线性调频信号的时频分布特征提取＊

付霖宇 张 鑫 程永茂 曹 建 崔欣辰

（海军航空工程学院兵器科学与技术系 烟台 264000）

1 引言

武器装备信息化程度的不断提高，现代战场的电磁环境日趋复杂，给复杂电磁环境下信号特征提取提出了新的要求［1～2］。本文通过分析典型线性调频（Linear Frequency Modulation，LFM）信号的模糊函数、短时Fourier变换（STFT）和 Wigner－Ville分布（WVD），归纳了LFM 信号的时频特征。相对传统的信号波形和频谱，时频特征具有能量聚集性高、噪声抑制性好的特点。理论分析和仿真实验表明，基于时频分析的特征提取方法能有效反映LFM信号的调频斜率、起始频率、调制带宽、分量个数等脉内调制参数，明显改进了噪声背景下对多分量LFM信号脉内调制参数的识别效果。

2 线性调频信号的时域和频域特征

信号在时域的基本形式通常表示为复数形式：

式中，A（t）为幅度；ω0（t）为瞬时角频率；φ（t）为初始相位；z（t）称为实信号s（t）＝A（t）cos［ω0t＋φ（t）］的解析信号。线形调频信号（LFM）是一种典型的非平稳信号，在雷达、通信、声纳等领域中有广泛应用［3］。一方面，LFM信号的一阶和二阶数字特征体现一种随时间变化的复杂性，另一方面，它的脉内调制频率具有随时间呈线性变化的规律性。理想LFM信号的时域复数形式表示如下：

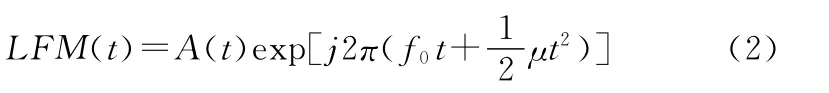
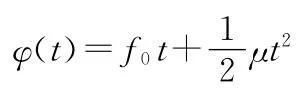
实际中多用矩形包络线形调频信号，在雷达中也称为Chirp信号［4］，其复数形式表示如下

通过计算机仿真，可直观得到典型LFM信号的波形和频谱，如图1所示。

由图1可见，无论是时域波形还是频域频谱，都不能清晰表征典型LFM信号的瞬时相位和瞬时频率等时变特征参数，更不能表征出信号调频系数等脉内特征参数。同时，LFM信号的时域波形和频域频谱对噪声很敏感，在混有信噪比为0dB白噪声的情况下，波形和频谱都有很大程度的模糊。因此，采用新的信号处理方法，兼顾表征LFM信号的脉内特征参数和抑制噪声干扰，对LFM信号的特征提取尤为重要。许多研究表明，时频分析方法能够有效满足这一要求［5～6］。

图1 LFM信号的波形和频谱

3 基于时频分析的LFM信号特征提取

3.1 LFM信号模糊函数时频分布特征

模糊函数（Ambiguity Function，AF）是波形设计的有效工具［7］，采用雷达“点目标”回波的数学模型，即仅考虑目标回波信号的时间延迟和多普勒频移，而不考虑面目标回波幅度的闪烁、传播路径的衰减、天线方向图调制等与信号形式无关的因素。从模糊函数的角度对信号进行特征分析，更容易把握其本质。

则A（τ，v）就是信号s（t）的模糊函数。如果对两个不同信号的瞬时互相关函数作Fourier反变换，相应得到两个信号的互模糊函数：

当v＝0时，上式就是通常的互相关函数R12（τ）。

模糊函数在（τ－v）平面即模糊域平面上反映了信号的时间和频率联合特性。准确地说，给出了两个空间点目标的时频联合分辨能力。这也体现了模糊函数的物理意义，即对单一目标，模糊函数给出了回波信号的时延－频移联合最优估计器输出的全景图形；对相邻的两个目标，模糊函数为信号的距离－速度联合分辨能力提供了一个保守估计。

LFM信号作为大时宽带宽积信号，即τB≥1，其模糊函数表达式为

式中，τ′是脉冲宽度；τ是时间延迟；v是多普勒频移；μ是调制斜率。LFM信号的模糊函数的能量分布为倾斜刀刃型，如图2。“倾斜”反映了线性调制的调频斜率，“刀刃”反映了信号包络的宽脉冲特性。

图2 LFM信号模糊函数

与图1相比，LFM信号的模糊函数体现了较高的能量聚集性，其主瓣宽度很大，几乎占据了整个时延轴，能量主要集中在主瓣中，如图2。模糊函数平面图的斜率即为LFM信号的调制斜率，模糊函数平面图在纵轴上投影的长度即为LFM信号的调制带宽，如图3。同时可见，LFM信号模糊函数的能量聚集并不是理想的，即存在一个在频移轴上的宽度，如果固定时延值，即沿平行频移轴进行切割，得到模糊函数的频移切片图，是具有辛格函数的包络，其主瓣宽度反映了一定时延下的距离分辨力，如图4。与没有脉内调制的单脉冲信号相比，相同条件下，LFM信号的距离分辨力是单脉冲信号的N倍，N＝τB。

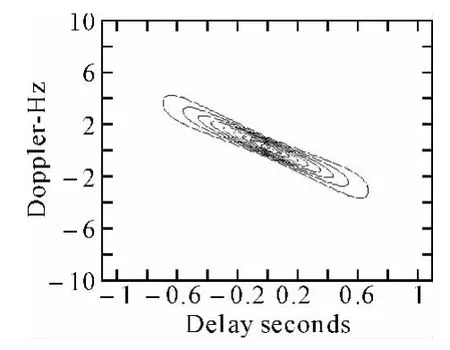
图3 LFM信号模糊函数在模糊域平面的投影

图4 LFM信号AF频移切片图

3.2 LFM信号短时傅立叶变换时频分布特征

信号z（t）的短时傅立叶变换（STFT）定义为

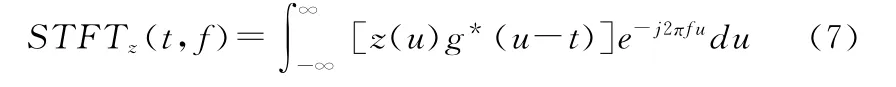
式中，＊代表复数共轭；g（t）是一个时间宽度很短的窗函数，它沿时间轴滑动。显然，如果取无穷长（全局）的矩形窗函数g（t）＝1，则STFT就是传统的傅立叶变换。

多分量LFM信号可表示为

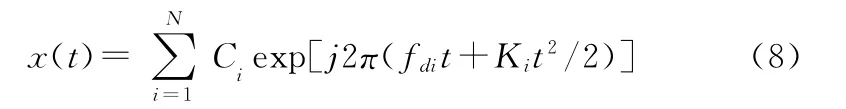
式中，N为LFM分量的个数；Ci、fdi和Ki分别表示第i个LFM分量的幅度、起始频率和调频斜率。LFM信号经短时傅立叶变换后，得到的时频域分布情况如图5、图6所示。

图5 单分量LFM信号STFT时频域分布特征（无噪声）

可以看出，通过STFT变换，LFM信号的调频斜率这个重要脉内参数能被直观的反映在时频域平面上。同时，由于STFT是线性变换，不产生二次交叉项［8］，所以STFT变换能较好地实现对多分量LFM信号脉内参数的特征提取。不过，由于滑动时间窗g（t）长度固定，决定了时间分辨力和频率分辨力不能同时达到最优，导致提取效果存在一定的局限性。

图6 两分量LFM信号STFT时频域分布特征（无噪声）

3.3 LFM信号Wigner－Ville时频分布特征

信号z（t）Wigner－Ville变换的定义为

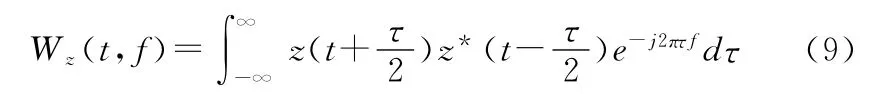
图7 单分量LFM信号Wigner－Ville时频域分布特征（无噪声）

图8 两分量LFM信号Wigner－Ville时频域分布特征（无噪声）

4 噪声对LFM信号时频分布特征的影响

为进一步研究复杂电磁环境对LFM信号时频分布特征的影响效果，本文建立了白噪声背景下多分量LFM信号模型，并对所建立模型的短时Fourier变换以及 Wigner－Ville分布的能量聚集性和抗噪声干扰性能进行仿真分析。仿真参数设置如下：LFM信号长度T＝256，两分量，调频范围（归一化后）分别为0.01～0.3，0.35～0.5，零均值高斯白噪声，方差σ2＝1，信噪比SNR＝0dB，时间平滑窗选用长度为25的Hamming窗。

噪声背景下多分量LFM信号可表示为

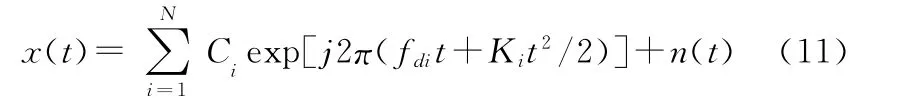
式中，N为LFM分量的个数，Ci、fdi和Ki分别表示第i个LFM分量的幅度、起始频率和调频斜率，为加性白噪声。

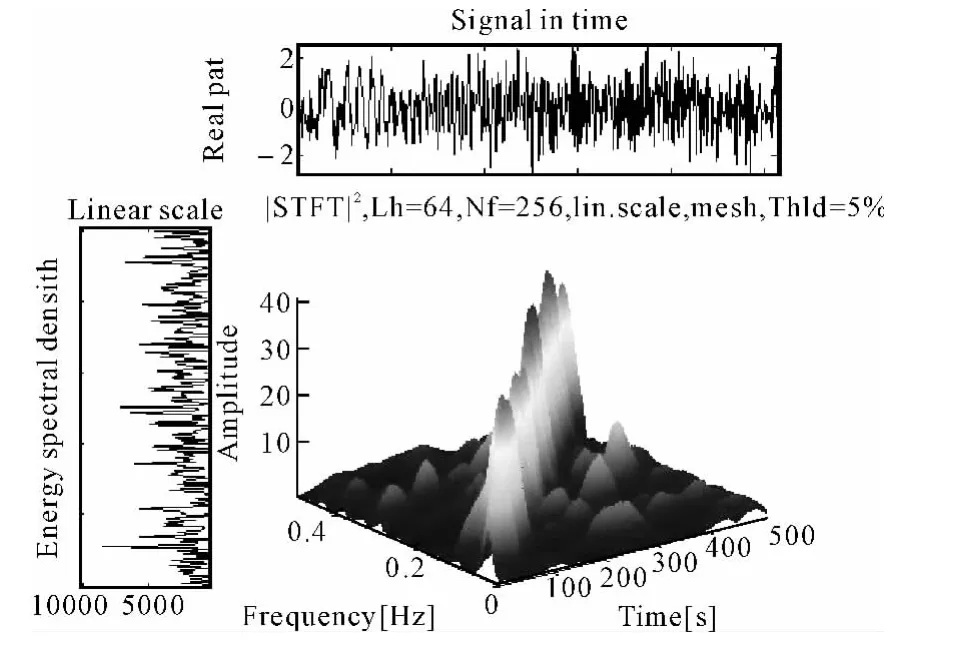
图9 单分量LFM信号STFT时频域分布特征（SNR＝0dB）

图10 两分量LFM信号STFT时频域分布特征（SNR＝0dB）

噪声背景下单分量和多分量LFM信号经短时傅立叶变换后，时频分布特征如图9、图10所示。

噪声背景下单分量和多分量LFM信号的Wigner－Ville时频分布特征分别如图11、图12所示。

图11 单分量LFM信号WVD Wigner－Ville时频域分布特征（SNR＝0dB）

图12 两分量LFM信号WVD Wigner－Ville时频域分布特征（SNR＝0dB）

与不含噪声的情况相比，噪声背景下，单分量LFM信号短时傅里叶变换时频分布中的背景电平有所增加，同时信号项的能量聚集性有所下降，如图9。同样的情况也存在于多分量LFM信号短时傅里叶变换时频分布特征中，但是没有出现交叉项，如图10。噪声背景下，单分量LFM信号Wigner－Ville时频分布特征中的背景电平已经不可忽略，同时信号项能量聚集性有所下降，如图11。对于含噪声的多分量LFM信号，其Wigner－Ville时频分布特征中交叉项所占比重更大，信号分量和交叉项会出现明显的混叠模糊，如图12。可见，噪声的存在降低了LFM信号的时间分辨力和频率分辨力，从而影响了对其调制斜率、起始频率、信号长度等脉内特征参数的提取效果。但从另一方面，可发现噪声背景下的LFM信号时频分布特征仍然能够体现出较强的能量聚集性，特别是多分量LFM信号短时傅里叶变换时频分布特征中不存在交叉项，利用这一特点可以实现对LFM信号的分量个数估计，提高信号特征提取效果。抑制多分量LFM信号噪声背景下时频分布中的交叉项，将是下一步工作需要研究和改进的地方。

［1］刘锋，孙大鹏，黄宇，等.基于改进Wigner－Hough变换的多分量LFM 信号特征提取［J］.北京理工大学学报，2008，28（10）：914－917.

［2］张葛祥，胡来招，金炜东.雷达辐射源信号脉内特征分析［J］.红外与毫米波学报，2004，23（6）：477－480.

［3］张贤达，保铮.非平稳信号分析与处理［M］.北京：国防工业出版社，1998，9：35－81.

［4］Bassem R.Mahafza.Radar Signal Analysis and Processing U－sing Matlab.Chapman＆Hall／CRC，2009：109－119.

［5］张贤达.现代信号处理.［M］.第二版.北京：清华大学出版社，2002，10：447－470.

［6］胡广书.现代信号处理教程［M］.北京：清华大学出版社，2004，11：52－60.

［7］林茂庸，柯有安.雷达信号理论［M］.北京：国防工业出版社，1984：93－113.

［8］吕宙.基于STFT的 Wigner－Ville分布交叉项抑制［J］.航天电子对抗，2010，26（3）：27－29.

［9］王冉，姜义成.一种针对多分量信号的复延迟型时频分布的实现方法［J］.电子学报，2012，40（1）：60－65.

［10］邹红星，戴琼海，李衍达，等.不含交叉项干扰且具有 WVD聚集性的时频分布之不存在性［J］.中国科学E辑，2001，31（4）：348－354.