带负载失衡调节的分布式粒子滤波算法研究＊

查巍巍 张 勇 应晓慧 周 源 李知杰

（武汉船舶通信研究所 武汉 430064）

1 引言

粒子滤波是一种基于蒙特卡罗方法和递推贝叶斯估计的统计方法［1］，适用于任何用到非线性、非高斯递推贝叶斯估计的系统，精度可以逼近最优估计。然而由于其计算量庞大，若采用集中式结构，粒子信息计算和通信所产生的巨大能耗会导致中心节点的瘫痪，因此有必要探索分布式的处理方法。

现有的分布式粒子滤波（Distributed Particle Fifter，DPF）主要包括两个方面：一种基于信息融合技术［2］即每个节点独立地运行完整的粒子滤波形成一次状态估计，然后交由融合中心进行融合；另一种基于并行计算，即将粒子滤波算法分解成可并行计算的进程，多个节点协作共同完成一次状态估计。由于粒子滤波的计算量巨大，单个节点上独立运行完整的粒子滤波算法将产生大量能耗，因此在硬件实现上多偏向于并行计算。图1给出了分布式粒子滤波并行计算模型原理图。

Bashi等设计了三种分布式粒子滤波算法［3］：全局DPF（Global DPF）、局部 DPF（Local DPF）和压缩 DPF（Compressed DPF）。三种方法都是基于并行计算，不同主要在于重采样，全局DPF和压缩DPF采用的是全局重采样，局部DPF采用的是局部重采样，然而若采用全局重采样则需要上传大量粒子的信息，增加了通信损耗，若采用局部重采样，会出现部分子节点由于粒子退化对全局状态估计作用甚小，导致最后全局估计误差偏大。

图1 分布式粒子滤波并行计算原理图

为了克服全局重采样带来的大通信量弊端，有人提出了基于GMM模型的DPF［4］，主要改进在于将传输的粒子用GMM分布近似，然而每次状态估计都需要计算GMM模型参数，会产生大量的计算能耗。因此，本文给出了一种精度能达到全局重采样，而且不需要传输具体的粒子信息的分布式粒子滤波并行计算方法。其中重采样算法来源于比例分配重采样［5］，只是将该算法在粒子集上并行实现，并采用粒子群优化算法解决部分子节点由于粒子退化带来的计算量失衡的问题。仿真结果表明，本文的算法在保持负载均衡的同时减少了通信损耗，并且可以取得较好的估计精度。

2 粒子滤波算法

粒子滤波器的本质是递归贝叶斯滤波，根据贝叶斯估计理论，一阶马 尔科夫序列｛xk｝k＝1，2，…的估 计问题是通过观测序列｛zk｝k＝1，2，…和状态转移概率密度函数p（xk｜xk－1）得到后验概率密度函数p（xk｜zk），即：

递推过程可分为预测和更新两步

预测：

更新：

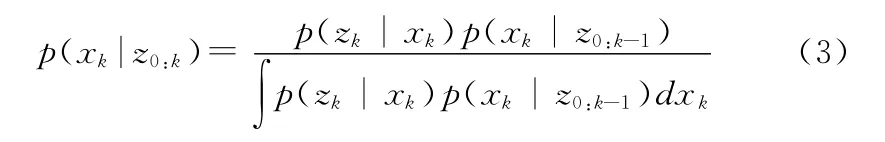
根据蒙特卡罗原理，后验概率分布可以用一系列带权重的随机采样点逼近，即：

由于从后验概率中很难直接采样，所以引入容易采样的已知分布的重要密度函数：q（x0：k｜z1：k）。粒子从重要密度函数中采样得到，则权值为

一般选择状态转移概率密度函数p（xk｜xk－1）作为重要密度函数。

粒子滤波算法由四步组成，描述如下：

1）采样。从p（xk｜xk－1）中采样N 个粒子

2）权值计算。

并且归一化

则可得k时刻的状态估计为

3）重采样。得到新的粒子集合

4）时刻k＝k＋1，转到第1）步。

3 分布式处理

分布式粒子滤波算法就是将式（6）～（8）在粒子集上并行计算，这三个式子可以很好的在粒子集上进行拆分计算，但是难点在于重采样的并行处理，不同的处理思想直接影响到分布式粒子滤波的执行效率和估计精度。

常见的重采样算法有多项式重采样算法［1］、残差重采样算法［6～7，9］、分层重采样算法［6～8］、系统重采样算法［6～9］。然而这些重采样算法都建立在粒子权重的累积分布函数，需要对全部的权重信息集中排序，若将这些算法并行计算，则不可避免进行粒子权重信息的交换，将带来额外的通信能耗。

Bolic提出比例分配重采样算法，该算法按粒子归一化的权重进行按比例采样，建立在权重和之上，不需要交换每个粒子的权重信息，因此可以很好地进行并行计算。

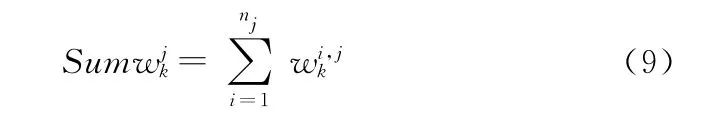
接下来可以进行并行重采样计算，伪代码如下：

Step1：中心节点根据子节点的权重和进行第一次一次比例分配重采样。

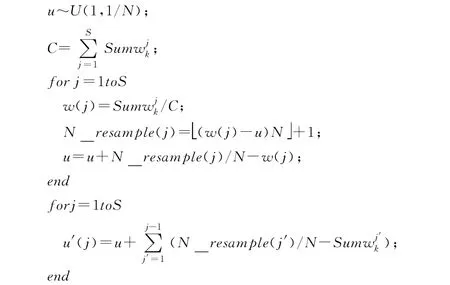
Step2：中心节点将 ｛u′ ，C｝变量传给子节点，子节点对本地粒子进行第二次比例分配重采样。

其中，中心节点产生的N＿resample（j）表示第j个节点上应该重采样N＿resample（j）个粒子，子节点上n＿resam－表示第j个子节点上第i个粒子应该被重采样n＿resa－次。而变量u′的计算刚好保证第j个子节点上通过step2得到的粒子数之和与中心节点计算的相同，即：

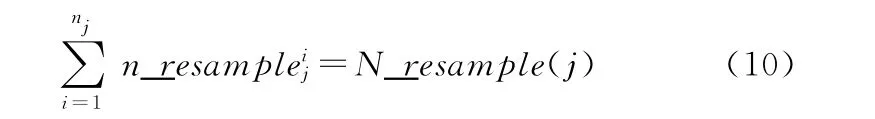
也就是说局部独立重采样的结果和全局重采样的结果是一样的，图2为并行比例分配重采样的计算原理图。

图2 并行比例分配重采样原理图

其中节点1和节点2的重采样并行进行，U和U′是并行重采样用到的随机数，u为集中式重采样用到的随机数，n（i）为第i个粒子重采样后重复的个数，若

则并行重采样和集中式重采样能得到相同的结果，即相同的n值。

根据Step1得

由集中式比例分配重采样算法得

即U′（1）＝u（6），以此类推，式（11）得证。也就是说比例分配重采样并行计算的关键在于每个子节点上第一个随机数的产生，即变量u′的计算。

4 分布式处理带来的负载失衡问题

通过第3节可以很好地将粒子滤波算法并行计算，但是在若干次估计之后，一些子节点由于粒子退化使得权重值和很小，中心节点比例分配重采样之后使得这些节点只需要产生少量的粒子数，即N＿resample很小，极端情况下，N＿resample只有一个非零，也就是说粒子全部在一个节点上计算，分布式粒子滤波退化成集中式粒子滤波。

上述问题可以理解为并行计算系统中的负载失衡问题，即有些节点超载，有些节点轻载，必须采用一种有效的算法均衡各个负载之间的计算任务。本文采用粒子群优化算法（PSO）对出现轻载的节点上的粒子进行优化，使其总体权重和变大，那么在下一次状态估计中，N＿resample变大，在一定程度上减轻负载失衡的问题。

粒子群优化算法（PSO）采用两个极值来更新粒子的速度和位置，使得整个粒子群向最优位置靠近，一个为个体极值Pi，即粒子本身从初始态到当前态经历的最优位置，另一个为种群极值Pg，即整个粒子群经历过的最优位置。利用粒子群优化算法对采样过程进行优化，使得粒子向高似然概率区域运动。本文采用一种改进的PSO算法［10］，该方法基于一个高斯分布来不断更新粒子的速度，其收敛性好于经典的PSO算法。

一般状态空间模型分为状态转移模型和量测模型：

其中wk和Vk分别为过程噪声和量测噪声，并且是相互独立，协方差分别为Qk和Rk的零均值加性噪声序列，因此真实值应该在观测值周围服从均值为0，协方差Rk的噪声分布，定义适应度函数为

PSO更新过程为

经过M次迭代后，粒子的最优值符合某阈值ε时，说明粒子群已经分布在真实状态附近，则停止优化。

图3是一个用PSO算法解决负载失衡问题的示意，其中总粒子数为100，子节点数为5。其中大括号内的值表示每个节点重采样之后的粒子数。

图3 利用PSO算法解决负载失衡的例子

引入PSO算法的目的是为了优化节点上的粒子，在一定程度上解决负载失衡的问题，但同时带来了额外的计算量，并且PSO优化打破了比例分配重采样的全局并行实现，而是用局部重采样代替，这样将会带来估计误差，在实际中需要权衡PSO优化的次数。

5 完整的分布式粒子滤波算法

用于粒子滤波的总粒子数目为N，用于计算的子节点数目为S，下标k表示时间点，i表示第i个粒子，j表示第j个子节点。则分布式粒子滤波算法描述如下：

1）子节点采样。

2）子节点权值计算。

聚合数据如下：

4）中心节点进行状态估计。

5）中心节点进行重采样。判断N＿resample，若N＿resample（j）／N＜α，则置位PSO优化标志，将数据｛u′，Ck，F｝发送到子节点，其中α为判断负载是否失衡的阈值，F为PSO优化的标志位。

6）子节点进行重采样。若F相应位被置位，那么相应子节点先调用PSO算法，然后采用局部DPF中的局部重采样；若F没有被置位，则子节点进行比例分配重采样。然后回到第1）步。

6 仿真结果与分析

本文在Matlab平台下进行仿真，假设目标在二维平面内做匀速直线运动。

系统状态转移方程为

观测方程为

其中，F＝［1T00 0100 001T 0001］；G＝［T2／20 T0 0T2／2 0T］；Wk为过程噪声，其协方差矩阵Q＝diag（0.12，0.12）；Vk为观测噪声，这里采用闪烁噪声，其密度函数可表示为

协方差P＝（1－eta）＊P1＋eta＊P2，其中

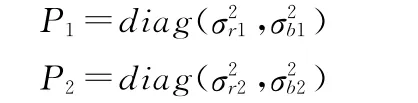
取σr1＝σr2＝50；σb1＝1°，σb2＝5°；eta＝0.1

初始状态选为x0＝［50000 300 50000 －100］T，仿真点为50，采用不同的粒子数和用于计算的子节点数，分别进行100次蒙特卡罗实验，本文的算法和其它两种分布式粒子滤波算法的误差比较如表1所示。

表1 不同粒子数、子节点数时的误差

表1中的结果可以表示成图4～图6的形式。分别对应节点数为1、5和10时三种算法的误差曲线。

图4 1个节点的误差曲线

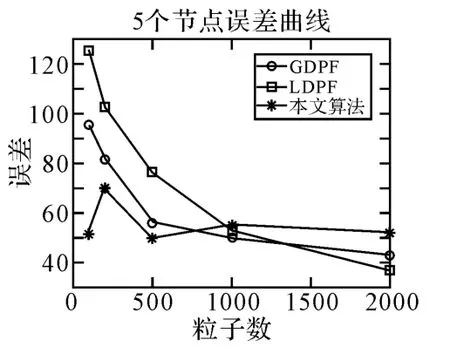
图5 5个节点的误差曲线

图6 10个节点的误差曲线

对于GDPF误差在粒子数增加到2000时可以降到很小，但是该算法需要传输大量的粒子，增加通信损耗；对于LDPF算法，由于局部重采样导致误差比同粒子数时GDPF的要大，但是不需要传送任何粒子信息，实现方便；本文所采用的算法也不需要传送任何粒子信息，并且由于引入了PSO算法，优化了用于估计的粒子，因此误差降低，但是PSO运行的次数越多会带来额外的计算开销。可以发现在粒子数为100时，容易出现负载失衡，也就是调用PSO算法的次数会很多，误差减小的同时带来很大的PSO计算开销，当粒子数上升为2000时，调用PSO算法的次数为0，也就是没有出现负载失衡的情况，此时误差值和节点数为1时相近，即比例分配重采样的并行计算可以达到与集中式计算同样的精度，证明了并行处理过程是可行的。

［1］Gordon N，Salmond D.Novel appr oach to non－linear and non－Gaussian Bayesian state estimation［J］.Procof I nstitute E lectr ic E ngineering，1993，140（2）：107－113.

［2］Coates M.Distributed particle fiflters for sensor networks.PIPSN，2004：99－107.

［3］Bashi A S，Jilkov V P，Li X R，et al.Distributed implementations of particlefilters［C］／／Proceeding of the Sixth International Conference of Information Fusion，2003，2：1164－1171.

［4］Sheng X H，Hu Y H.Parameswaran Ramanathan.Distributed particle filter with GMM approximation for multiple targets［C］／／4th International Symposium on.Information Pocessing in Sensor Networks，2005：181－188.

［5］Bolic M，Djuric P M，Hong S J.Resamping alogorithms and architectures for distributed partical filters［J］.IEEE Trans.on Signal Processin，2005，53（7）：2442－2450.

［6］R V Merwe，A Doucet，Nando De Freitas，et al.The Unsented Particle Filter［R］／／Technical Report，CUED／F－INPENG／TR 380.UK：Engineering Department，Cambridge University，2000.

［7］J D Hol.Resampling in Particle Filters［R］／／Intership report，LiTH－ISY－EX－ET－0283－2004.Sweden：Link ping University，2004.

［8］Miodrag Bolic'，Peter M Djuric'，Sangjin Hong.New Resampling Algorithms for Particle Filters［J］.ICASSP2003（S1845－5921），2003，2：589－592.

［9］KROHLING R A.Gaussian swarm：a novel particle swarm optimization algorithm［C］／／Proceedings of the IEEE Conference on Cybernetics and Intelligent Systems（CIS）.Singapore：IEEE Press，2004：372－376.

［10］Peng zhang，Ming Li，Yan Wu.An improved particle filter algorithm based on Markov Random Field modeling in stationary wavelet domain for SAR image despeckling［J］.Pattern Recognition Letters，2012，33（10）：1316－1328.