一种基于MAD的鲁棒性分形维数计算方法及图像识别应用

吴海燕，张陈陈

(深圳大学数学与计算科学学院，广东 深圳 518060)

0 引言

分形几何(Fractal Geometry)是由法国数学家B.B.Mandelbrot开创出的一门新的数学分支［1-2］，维数是分形几何理论中最重要基本概念之一。对于某一集合，一般而言，如果它的Hausdorff维数严格大于其拓扑维数，则该集合可称为分形集合。考虑n维欧氏空间的有界集A，如果集合A表示为自身的Nr个互不重叠的子集的并集时，则得出集合A具有自相似性。而此时，集合A的分形相似维数D可由关系式(1)表示［1-2］:

其中，r表示所有坐标方向上的尺度因子，Nr表示有界集A的互不覆盖的子集数目。然而，自然界的景物并不严格地满足自相似性，它们仅呈现出某种统计意义上的自相似性，因此很难直接利用式(1)计算分维数。

文献［3-8］提出了一些计算图像分形维的方法。例如，Sarkar等［3］提出了一种差分盒计数法(DBC)，该方法给出了较宽的分形维动态范围和较高的计算效率，但缺点是对噪声非常敏感;此后，Lee等［7］提出了一种鲁棒的差分盒计数法(RDBC)，该方法对高斯噪声具有很好的抗噪性，但不适用于椒盐噪声等其他噪声情况。

本文提出一种基于中值绝对偏差(MAD)的差分盒计数法(MAD-DBC)，该方法针对椒盐噪声具有很好的鲁棒性，能对椒盐噪声图像进行可靠的分形维估计。

1 传统(鲁棒)差分盒计数法

差分盒计数法(DBC)的基本思想是通过计算覆盖图像灰阶表面所需的盒子数来确定分形维。对于面积为M×M的图像，若它被划分成大小为s×s的网格，其中s是介于1到M/2之间的整数，则r=s/M。若把灰度图像的像素看成三维空间的一个坐标(x，y，z)，其中(x，y)为二维图像的像素点的坐标，z为图像灰度值。则认为在每一个网格上都堆叠了一系列体积为s×s×h的小盒子，其中盒子高h可通过图像的总灰度级G来计算:［G/h］=［M/s］，通常G表示图像的最大灰度级与最小灰度级之差，［x］代表小于x的最大整数。若在图像的第(i，j)个网格内灰度最小值和灰度最大值相对应的分别落在第l个和第u个小盒子内，则覆盖第(i，j)区域所需盒子数目nr(i，j)为:

统计图像的盒子总数Nr为:

对不同的尺度r，得到相应盒子数Nr的值。由式(1)的定义，采用最小二乘法可以拟合出log(Nr)～log(1/r)的斜率，即可得到对应图像的分维值D。

在DBC基础上，基于标准差的鲁棒差分盒维数法(RDBC)采用网格中像素的灰阶标准差替代最大与最小灰阶之差，来计算此网格中图像灰阶表面所占的盒子个数。具体地，若给定尺度缩放的比例为r，设图像第(i，j)个网格中像素的灰阶标准差为σr(i，j)，则由下式计算盒子数nr(i，j):

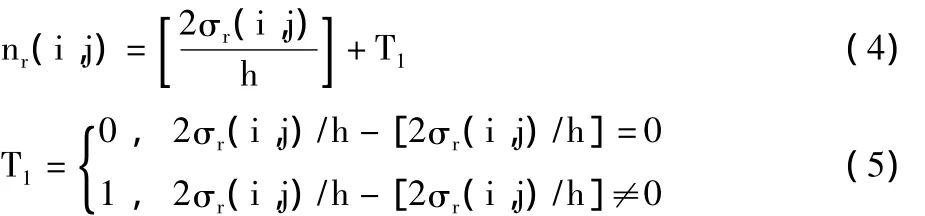
然后利用式(3)计算相应的总盒子数Nr，同DBC一样利用式(1)的定义，采用最小二乘法可以拟合出log(Nr)～log(1/r)的斜率，所得斜率即为估计的图像分形维D。

基于标准差的鲁棒差分盒维数法证明对高斯噪声的敏感性较小，从而使得RDBC对高斯噪声具有较好的抗噪性。然而对于诸如椒盐噪声，这种噪声对灰阶标准差的影响较大，从而将导致利用RDBC对加有椒盐噪声的图像效果变差。

2 改进的MAD鲁棒性差分盒计数法

在DBC和RDBC算法中，在计算图像第(i，j)个网格中的盒子个数nr时，采用的是此网格中最大与最小灰阶之差或像素值标准差，但都易受到椒盐噪声的干扰。根据椒盐噪声的特点，它是将图像的中灰度值变化到一个比较极端的值，因此会使得原有的最大最小像素值都变化，图像加噪以后，在某些网格中最大的灰度值u比原来的最大灰度值更大，最小灰度级l比原来的最小灰度值更小，一般情况下，在网格尺度不变，即压缩比例r不改变下，nr(i，j)=u-l+1的计算值偏大，从而使得Nr的估算值偏大。于是，当log(1/r)不变时，log(Nr)增大，从而使得采用最小二乘法可以拟合出log(Nr)～log(1/r)的斜率偏大，即分形维数通常将偏大。类似地，椒盐噪声往往使得像素值标准差变大，从而影响RDBC分形维数估计。

CMV感染是艾滋病患者最常见的疱疹病毒感染，可分为CMV血症和器官受累的CMV病。CMV可侵犯患者多个器官系统，包括眼睛、肺、消化系统、中枢神经系统等，其中CMV视网膜脉络膜炎是艾滋病患者最常见的CMV感染。

由于中值偏差(MAD)具有对椒盐噪声鲁棒性特点，本文提出的改进差分盒维数法将鲁棒差分盒维数法中的网格中的灰阶标准差σr(i，j)用灰阶的中值绝对偏差(MAD)代替。通常，中值绝对偏差(MAD)用下列公式计算［14］:

其中，med(uij)表示计算第(i，j)个网格中图像像素值的中值。若给定尺度缩放的比例为r，设图像第(i，j)个网格中像素的灰阶中值绝对偏差为ρr(i，j)，则由下式计算盒子数nr(i，j):

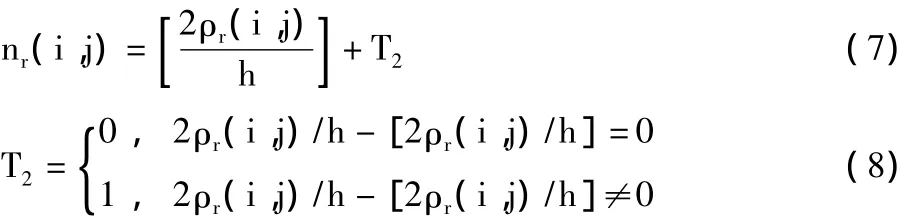
随后，利用式(3)计算相应的总盒子数目Nr。同DBC一样利用式(1)的定义，采用最小二乘法可以拟合出log(Nr)～log(1/r)的斜率，所得斜率即为估计的图像分形维D。综上讨论，改进算法如下:

3 数值实验

3.1 分形维特征矢量

单一的分形维数并不能完全区分不同图像纹理，而基于小波的多分辨率分析的分形特征矢量提取能克服单一分形维数的缺点。在不同的分辨率下对图像求取分形维数，构成特征矢量，即利用小波变换对图像进行频域分解［8］，对分解后的各部分频域图像求取它们的分形维数，作为一类图片的特征向量。

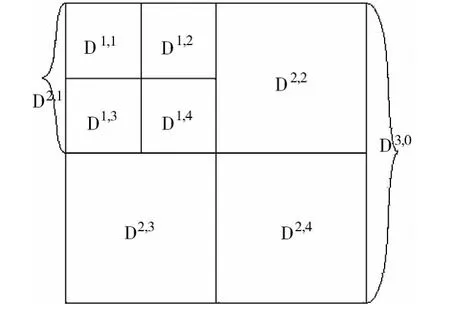
图1 小波分解后特征提取

图2 Brodatz纹理图像

如图1所示，设原始图像的分形维为D3.0，第一级分解的 LL1，HL1，LH1和 HH1的分形维分别为D2.1，D2.2，D2.3，D2.4，第二级分解的 LL2，HL2，LH2，HH2的分形维分别为 D1.1，D1.2，D1.3，D1.4。于是，分形维特征向量为:(D3.0，D2.1，D2.2，D2.3，D2.4，D1.1，D1.2，D1.3，D1.4)

3.2 自然纹理图像分类

从Brodatz纹理库［12］中挑选了16种自然纹理图像，如图 2所示，(D3，D5，D7，D13，D18，D31，D24，D51，D56，D66，D72，D87，D94，D99，D102，D112)作为数据集。在每种纹理图像中，分割选取30幅大小为256×256像素的样本图像，其中20幅用于分类器的训练，另10幅用于测试，组成320幅训练图像和160幅测试图像。

表1 噪声强度

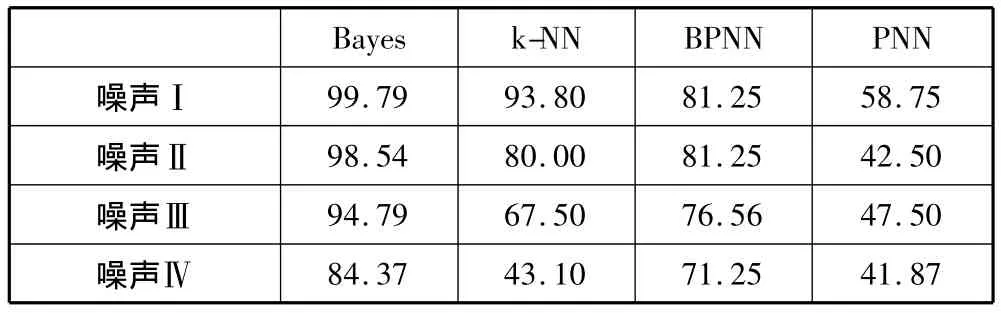
表2 Sarkar DBC法对不同噪声强度图像的分类识别率%

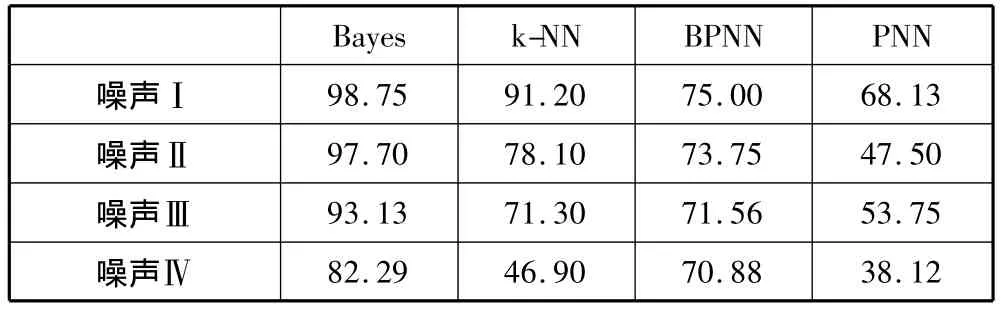
表3 Lee鲁棒差分盒维数法对不同噪声强度图像的分类识别率%

表4 本文改进差分盒维数法对不同噪声强度图像的分类识别率%

通过重复分类实验，对表2、表3分析可知，差分盒维法和鲁棒差分盒维法，在椒盐噪声强度低时，受影响不大，但随着噪声参数的增大，分类正确率明显下降。结合表4可知，利用本文改进的方法计算的分形维数，分类正确率总体上比其他几种方法都要高，特别是在较高噪声情形下，仍能保持较高的识别率。上述结果显示，对于椒盐噪声，新方法具有更好的噪声鲁棒性，可保持更高更稳定的分类识别能力。

4 结束语

本文探讨一种针对椒盐噪声的鲁棒性分形维数计算方法，该方法利用MAD进行差分盒计数，对椒盐噪声具有很好的鲁棒性特点。利用多分辨率的DBC、RDBC和本文 MAD-DBC对椒盐噪声的16种Brodatz纹理图像进行分类，实验结果表明，本文提出的MAD-DBC对椒盐噪声情形具有更高的识别率和更好的噪声鲁棒性。

［1］Mandelbrot B B.The Fractal Geometry of Nature［M］.W.H.Freeman and Company，1982.

［2］张济忠.分形(第2版)［M］.北京:清华大学出版社，2011.

［3］Sarkar N，Chaudhuri B B.An efficient differential boxcounting approach to compute fractal dimension of image［J］.IEEE Transactions on Systems，Man and Cybernetics，1994，24(1):115-120.

［4］Bisoia A K，Mishrab J.On calculation of fractal dimension of images［J］.Pattern Recognition Letter，2001，22(6-7):631-637.

［5］Li J，Du Q，Sun C.An improved box-counting method for image fractal dimension estimation［J］.Pattern Recognition，2009，42(11):2460-2469.

［6］杨词银，许枫.一种抗噪分形维计算方法及其在声纳图像识别中的应用［J］.应用声学，2008，27(2):95-101.

［7］Lee W L，Hsieh K S.A robust algorithm for the fractal dimension of images and its applications to the classification of natural images and ultrasonic liver images［J］.Signal Processing，2010，90(6):1894-1904.

［8］Martínez-López F，Cabrerizo-Vílchez M A，Hidalgo-Álvarez R.A study of the different methods usually employed to compute the fractal dimension［J］.Physica A，2002，311(3-4):411-428.

［9］孙延奎.小波分析及其应用［M］.北京:机械工业出版社，2005.

［10］董立岩，苑森淼，刘光远，等.基于贝叶斯分类器的图像分类［J］.吉林大学学报:理学版，2007，45(2):249-253.

［11］余肖生，周宁，张芳芳.基于KNN的图像自动分类模型研究［J］.中国图书馆学报，2007(1):74-76.

［12］孙君顶，李琳.基于BP神经网络的医学图像分类［J］.计算机系统应用，2012，21(3):160-162，212.

［13］Brodatz P.Textures:A Phontographic Album for Artist and Designers［M］.New York:Dover，1966.

［14］Lu J，Ye Z，Zou Y.Huber fractal image coding based on a fitting plane［J］.IEEE Transactions on Image Processing，2013，22(1):134-145.