一个简化的混沌系统及其控制器设计

吴凤娇，张建伟，王 雷

(西北农林科技大学水利与建筑工程学院，陕西 杨凌 712100)

0 引言

世界的本质是非线性的，非线性是产生混沌的必要条件。自从1963年Lorenz［1］第一次在三维系统中发现混沌吸引子以来，混沌引起了人们的广泛关注。人们发现并提出了很多新的混沌系统，具有代表性的包括1999年陈关荣等［2］发现存在混沌吸引子的Chen系统，2002年吕金虎等［3］发现的Lü系统和2004年刘崇新等［4］进一步提出的Liu系统。随着计算机科学的不断发展，人们对系统的混沌认识逐渐加深。

近年来，相关学者构造了很多新的四维混沌系统［5-7］，但对只含有一个立方项的四维混沌系统的研究不多，对其控制进行的文献就更少。人们对于如何控制混沌开展了大量的研究，并已经设计出许多控制方法，包括线性反馈控制方法、模糊控制方法、滑模控制方法以及主动控制方法等［8-13］。本文首先在磁弹体混沌系统的基础上，构造一个新的四维混沌系统，并对其混沌特性进行动力学分析，证实该系统混沌的存在性。并提出一种新的滑模控制方法用于该系统的控制，通过Matlab数值仿真验证所设计的控制器的有效性。

1 混沌系统的提出及分析

1.1 系统的混沌数学模型

混沌是非线性动力系统所特有的行为，而含有非线性项是非线性动力系统的必要条件，故非线性项对系统能否出现混沌具有重要作用。磁弹体系统［14］的混沌模型为:

本文在公式(1)磁弹体系统的基础上，通过引入部分线性项，构造只含有一个立方项的新四维动力系统为:

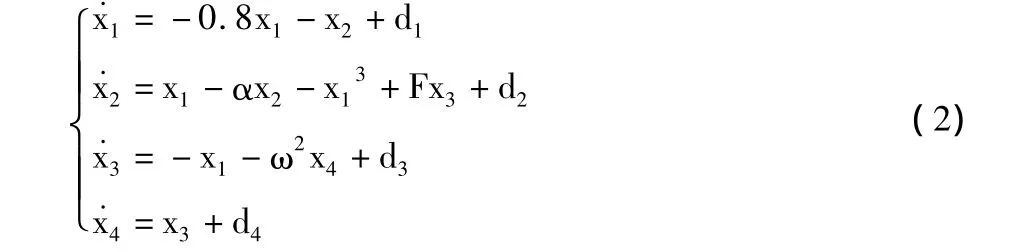
其中，α、F、ω 均是大于零的常数，d1、d2、d3、d4为外界扰动，它们都是有界的，即|di|≤δ，δ为常数。为不失一般性，此处取随机扰动 d1=0.2;d2=0.3*sin(t);d3=0.4*cos(t);d4=0.4。当 α =0.3，F=0.365，ω =1.2时，系统的三维相轨迹曲线如图1所示。

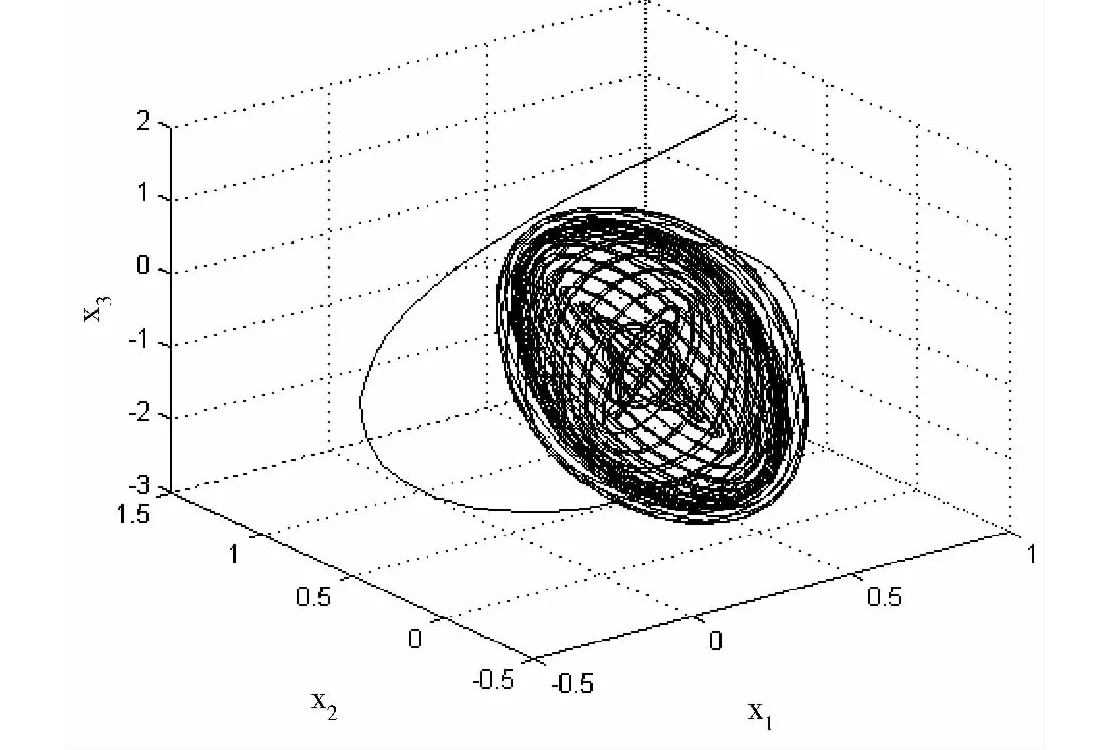
图1 公式(2)系统的x1-x2-x3相轨迹运动曲线

1.2 系统的混沌特性分析

1.2.1 耗散性分析

对系统进行耗散性分析有助于更好地发现系统的混沌特性，对式(2)做梯度运算可以得到:

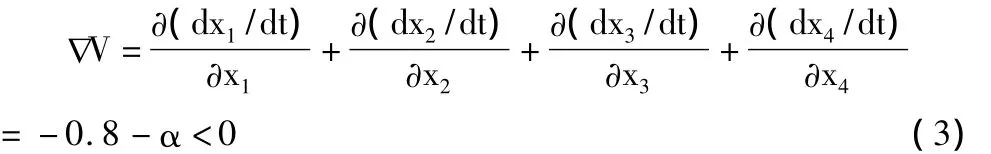
经过上述分析计算可以看出，公式(2)系统的梯度小于零，即系统具有耗散性结构，随着时间的推移，系统的运动轨迹最终将会趋于一个体积为零的极限吸引子上，收敛的速度是以指数-0.8-α的形式收敛到零。

1.2.2 Poincaré截面分析

利用Poincaré截面可以更好地认识系统的混沌特性，是一种经典的混沌系统分析技术。可以通过观测庞加莱截面上点的分布对系统进行定性分析，做出公式(2)系统在x1-x4平面点的分布情况如图2所示，在图2中点的分布是成片分形密集的，说明系统存在混沌行为。

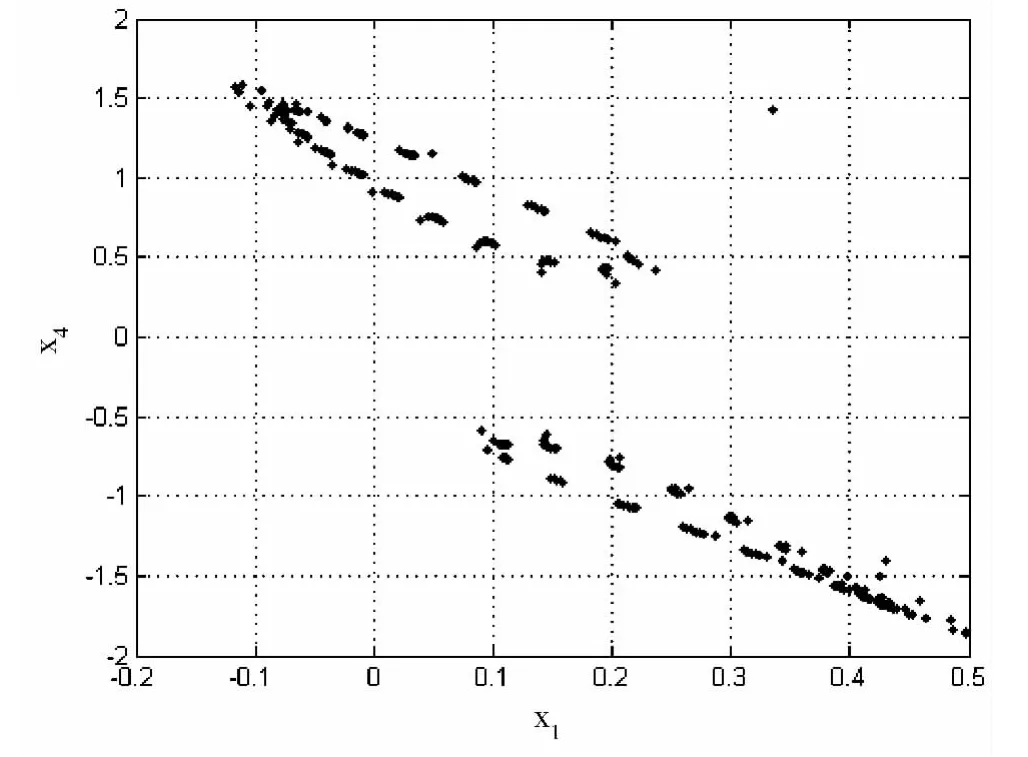
图2 公式(2)系统的庞加莱截面

1.2.3 Lyapunov 指数

李雅普诺夫是一种非常经典的非线性动力学系统分析技术，通过观察李雅普诺夫随系统参数变化的动态规律，可以非常方便地对系统是否存在混沌做出判断。当系统的李雅普诺夫指数有一个大于零时，称其为混沌系统;当系统存在2个李雅普诺夫指数大于零时，称其为超混沌系统。当 α =0.3，F=0.365，ω =1.2时，做出公式(2)系统的李雅普诺夫指数随参数F的变化规律如图3所示，可以从图3中明显地看出，系统有一个Lyapunov指数大于零，因此公式(2)系统存在混沌特性。

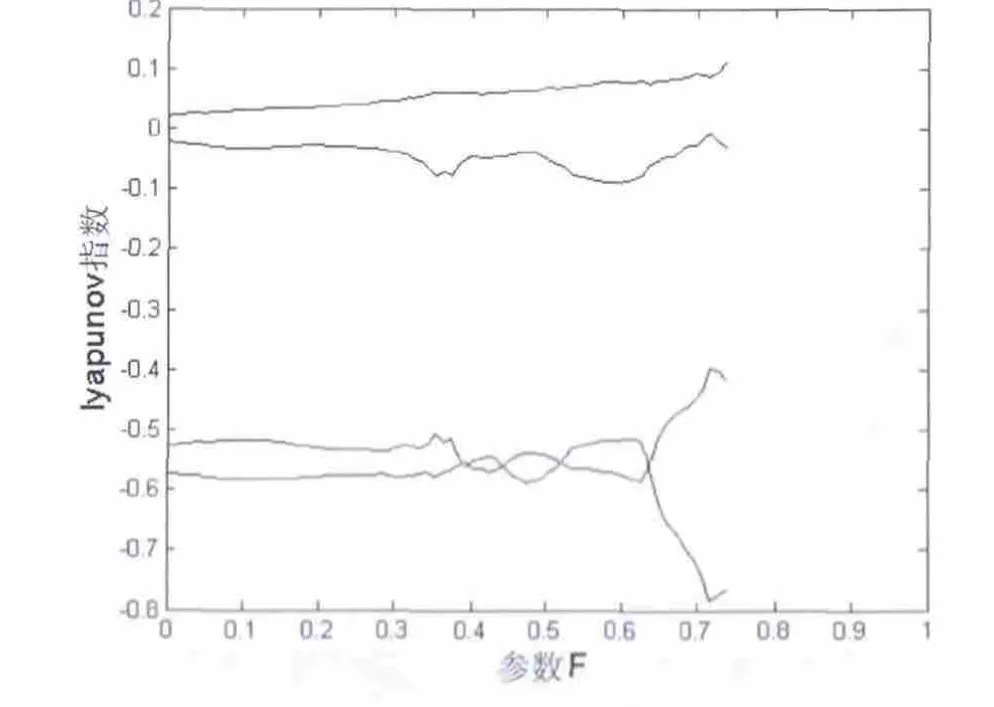
图3 公式(2)系统的Lyapunov指数谱

2 系统混沌模型的滑模变结构控制

2.1 系统的受控模型

公式(2)系统在控制器作用下的受控模型为:

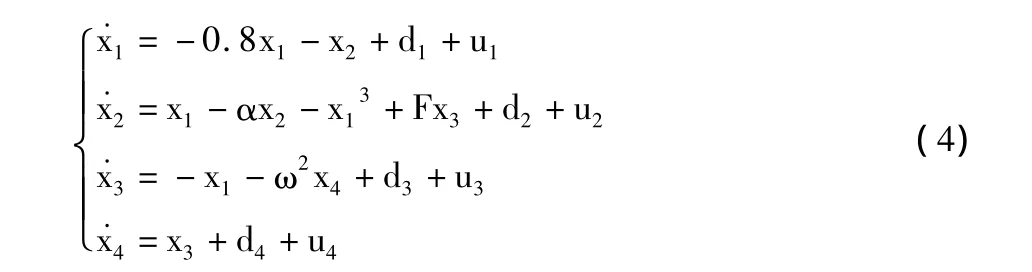
式(4)中 u1、u2、u3、u4为待设计的控制器，定义如下矩阵:

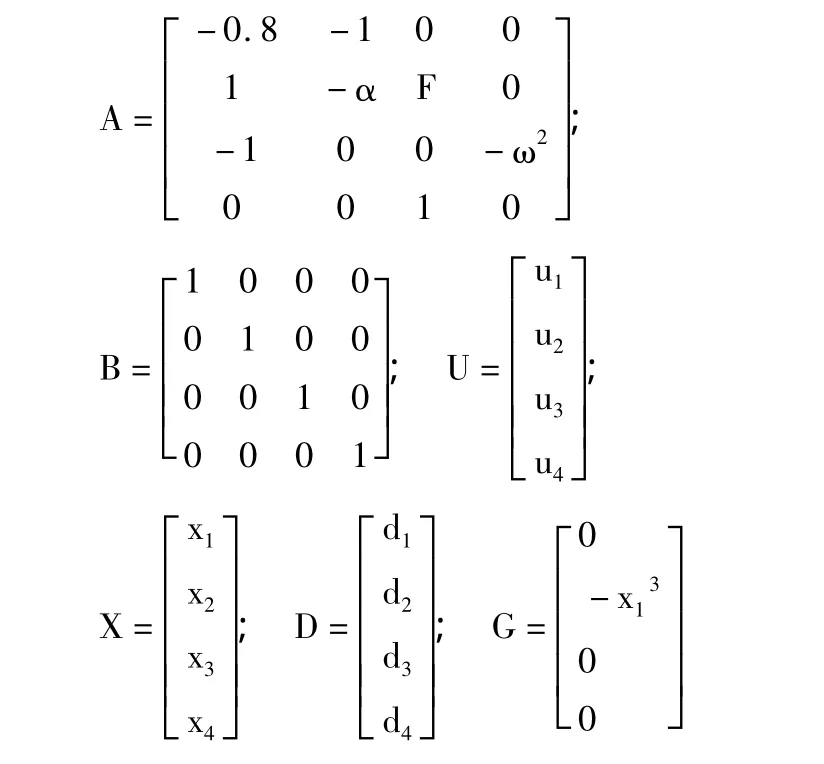
其中，A为系统的线性矩阵，B为系统的控制矩阵，U为控制向量，X为状态向量，D为外界扰动向量，G为系统的非线性向量。

在控制器输入为0时，系统的状态轨迹曲线以x1为例如图4所示，可以看出，公式(2)系统在未加控制器时，其运动轨迹是非周期的随机运动。因此设计目标就是在加入控制器后，能够将公式(2)系统控制到指定的固定点或周期轨道。

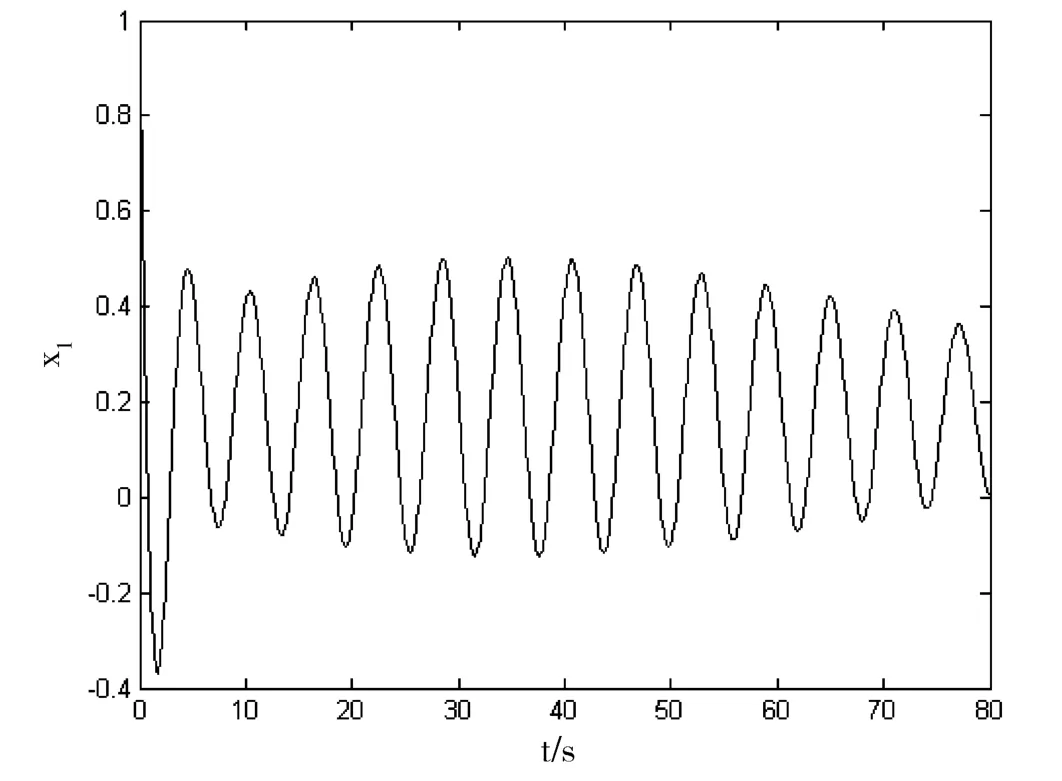
图4 受控前公式(2)系统状态变量的时域图

2.2 控制器的设计

滑模控制器的设计分为2步:(1)等价控制器的设计，通过构造滑模面使系统达到期望的轨道;(2)不连续的趋近率的设计，保证系统在滑模面外的运动都能在有限的时间内达到滑模面上，保证系统的鲁棒性。

控制的目标是使系统的状态X=［x1x2x3x4］T跟踪期望的状态 Xd=［xd1xd2xd3xd4］T，因此，定义系统的跟踪误差:

其中，E= [e1e2e3e4]T为系统的跟踪误差向量。可以得出误差动力系统为:

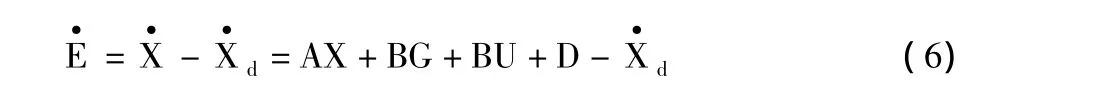
设计滑模面S=S(E，t):

其中，需要满足条件 det(KB)≠0，此处取 K=diag(1，1，1，1)，并且满足 A-BL 为负定矩阵。

总的滑模控制器设计为:

其中，ueq是等效控制器，ud为不连续的趋近律。

在滑模状态下，必须满足:

在不考虑外界扰动时，由式(6)、式(7)和式(9)可得:

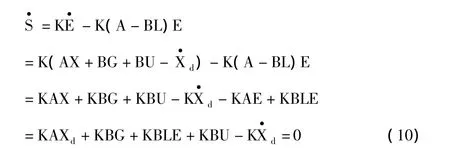
因此由式(10)可以得到等效控制器:

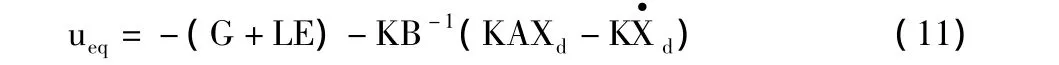
为了保证系统在滑模面上运动的鲁棒性，设计不连续的趋近律:

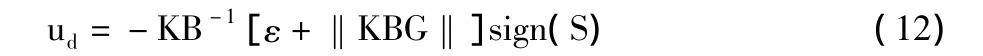
将式(11)和式(12)代入式(8)可得，系统总的控制器设计为:

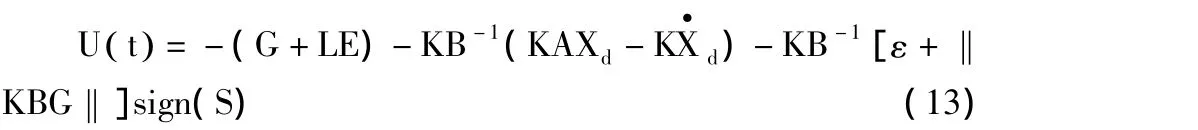
其中，sign( x)是 x的符号函数，当 x＞0，sign( x)=1;当 x=0，sign( x)=0;当 x＜0，sign( x)=-1。

命题 若ε为常数，且满足ε＞δ，则前述设计的式(13)控制器可将公式(2)系统从混沌态控制至稳定运行状态。

证明 李雅普诺夫函数选择为:

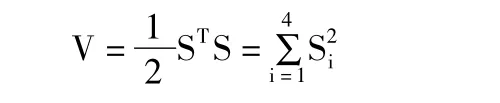
从式(7)和式(13)可以得到:

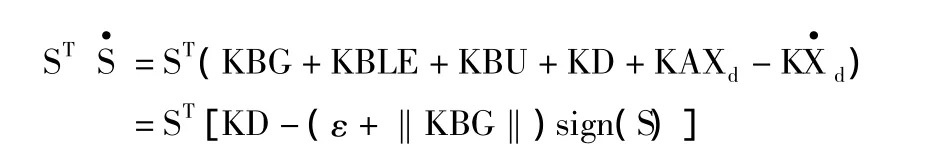
证毕。

从上面的证明可以看出，设计的式(13)控制器具有很好的鲁棒性，具有对外界干扰不敏感的优点。

2.3 数值模拟

为将公式(2)系统从混沌态控制到期望的目标，取矩阵 A-BL的特征根为 P=［-5，-4.99，-5，-5.01］，故可确定矩阵:

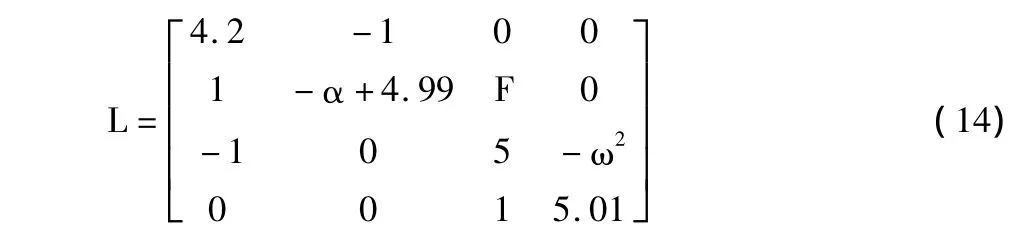
根据式(7)可确定滑模面如下:

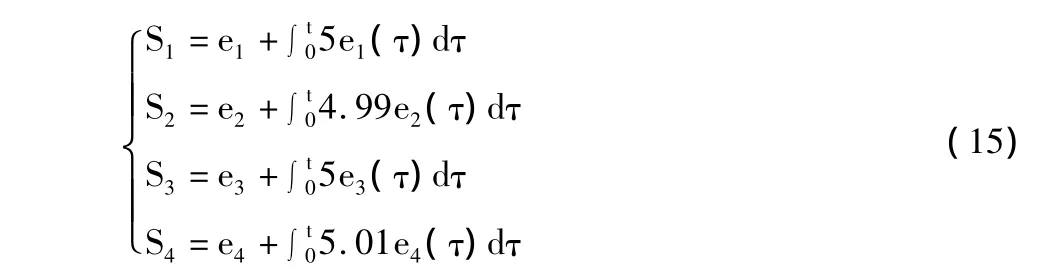
系统的初值取为［x(0)，y(0)，z(0)，u(0)］=［1，1，1，1］，期望目标 xd1=xd2=xd3=xd4=xd。可以得到控制器为:

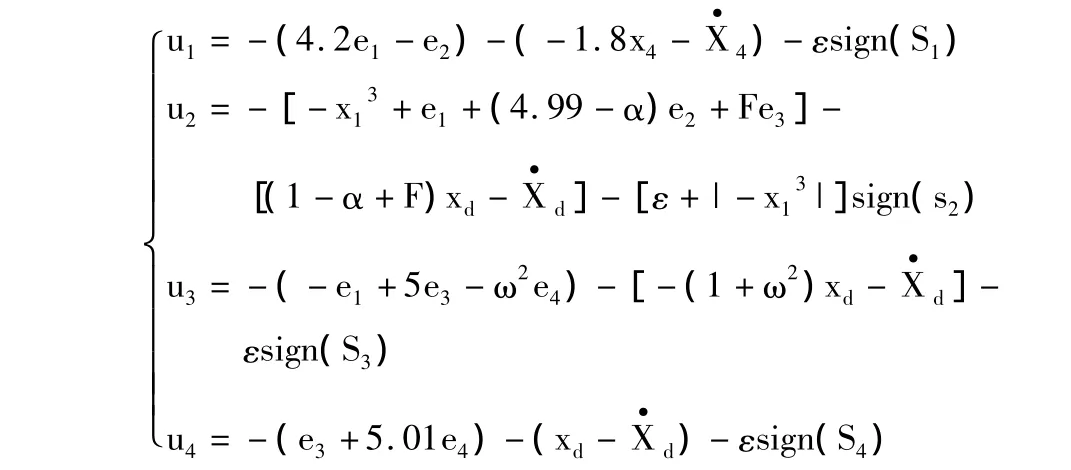
2.3.1 控制到固定点

在这里取参考状态xd=0.3为例，在刚开始不加入控制器，等系统运行至t=10s时加入控制器，采用Matlab数值模拟绘制系统的状态变量和滑模面的运动轨迹分别如图5和图6所示，此时对应的参数取值为 α =0.3，F=0.365，ω =1.2，ε =7。

通过观察图5和图6系统的状态变量以及滑模面时域图可知，系统在加入控制器后在很短的时间内最终被控制至参考状态xd=0.3，证明所设计控制器的有效性。

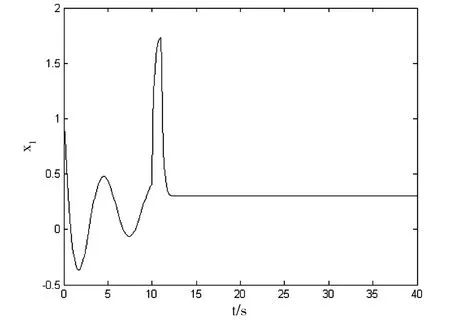
图5 受控后公式(2)系统状态变量的时域图(xd=0.3)

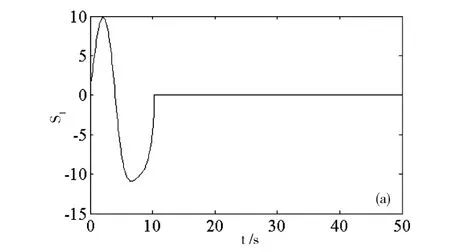
图6 受控后公式(2)系统滑模面的时域图

2.3.2 控制到周期轨道

在这里取参考状态xd=0.5sin(0.5t)为例，在刚开始不加入控制器，等系统运行至t=10s时加入控制器，采用Matlab数值模拟绘制系统的状态变量的运动轨迹如图7所示。

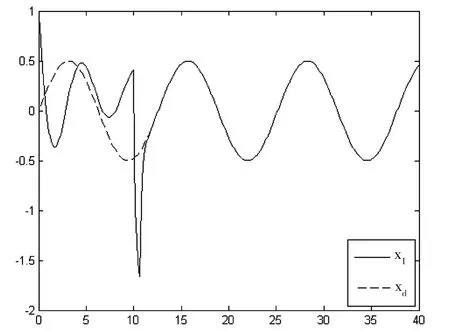
图7 受控后公式(2)系统状态变量的时域图(xd=0.5sin(0.5t)

通过观察图7系统的状态变量时域图可知，系统在加入控制器后在很短的时间内最终被控制至参考状态 xd=0.5sin(0.5t)，证明所设计控制器的有效性。

3 结束语

本文构造了一种只含一个立方项的非线性系统，通过对其相图、耗散性、Lyapunov指数等动力学特性进行分析，证实了该系统的混沌存在性。并设计了一种新的滑模控制方法对其混沌运行轨迹进行控制，分别将其控制到期望的固定点和周期轨道，理论分析和Matlab数值仿真结果完全一致，证实了设计的控制器的合理性和有效性。

［1］Lorenz E N.Deterministic nonperiodic flow［J］.Journal of the Atmospheric Sciences，1963，20(2):130-148.

［2］Chen G R，Ueta T.Yet another chaotic attractor［J］.International Journal of Bifurcation and Chaos，1999，9(7):1465-1466.

［3］Lu J H，Chen G R.A new chaotic attractor coined［J］.International Journal of Bifurcation and Chaos，2002，12(3):659-661.

［4］Liu C X，Liu L，Liu T，et al.A new butterfly-shaped attractor of Lorenz-like system［J］.Chaos，Solitons and Fractals，2006，28(5):1196-1203.

［5］张宇辉，齐国元，刘文良，等.一个新的四维混沌系统理论分析与电路实现［J］.物理学报，2006，55(7):3307-3313.

［6］Chen Y，Yang Y Q.A new four-dimensional chaotic system［J］.Chinese Physics B，2010，19(12):120510.

［7］王发强，刘崇新，逯俊杰.四维系统中多涡卷混沌吸引子的仿真研究［J］.物理学报，2006，55(7):3289-3306.

［8］Aline S P，Marcelo A S.A multiparameter chaos control method based on OGY approach［J］.Chaos，Solitons ＆Fractals，2009，40(3):1376-1390.

［9］Sadeghpour M，Khodabakhsh M，Salarieh H.Intelligent control of chaos using linear feedback controller and neural network identifier［J］.Communications in Nonlinear Science and Numerical Simulation，2012，17(12):4731-4739.

［10］王校锋，薛红军，司守奎，等.基于粒子群算法和OGY方法的混沌系统混合控制［J］.物理学报，2009，58(6):3729-3733.

［11］Wang C C，Pai N S，Yau H T.Chaos control in AFM system using sliding mode control by backstepping design［J］.Communications in Nonlinear Science and Numerical Simulation，2010，15(3):741-751.

［12］Liu H，Yu H J，Xiang W.Adaptive fuzzy nonlinear inversion-based control for uncertain chaotic systems［J］.Chinese Physics B，2012，21(12):120505.

［13］郑珍，谭满春.不确定参数时滞混沌系统的自适应反同步［J］.计算机仿真，2012，29(12):207-210.

［14］王琳.磁弹体混沌系统的电路实现及混沌控制［D］.长春:东北师范大学，2011.