一种组合神经网络在结构优化中的应用

王矅辰，纪爱敏，张大伟，郭聪聪

（河海大学机械工程学院，江苏常州 213000）

0 神经网络优化方法的研究和存在不足

结构优化设计是工程中的重要环节，建立以性能最大化，成本最小化的多目标优化设计模型，利用有限元计算和优化算法在指定参数区域内找出设计参数的Pareto最优解集的方法逐渐被工程中所采用。然而面对一些复杂的模型，和大量接触的非线性问题，有限元的重复迭代计算存在大量的时间成本的投入，以神经网络学习替代有限元计算为有效的方法。参考文献［1］介绍了通过BP神经网络的学习，结合遗传算法的多目标优化方法，并应用与对液压机的上梁优化中，提高了优化效率;参考文献［2］介绍了利用RBF神经网络学习取代有限元计算的可靠性，并以25杆桁架做为算例。然而目前大部分研究停留在整体方法介绍，对于提高神经网络应力预测准确度的研究却较少涉及，而神经网络应力预测的精度却是整个方法成功与否的关键。本文在挖掘机动臂仿真分析基础上，简述BP神经网络和RBF神经网络的预测特点，并提出BPRBF组合的神经网络，进一步扩展RBF神经网络的应用范围和BP神经网络的预测精度。

1 神经网络的原理简介

1.1 BP神经网络的基本原理

BP神经网络（back propagation neural network），被称为误差方向传播网络，它是由非线性变换单元组成的前馈网络，由输入层、中间层和输出层组成。BP神经网络的学习过程由两部分组成:正向传播和反向传播。当正向传播时，信息从输入层经过隐层单元处理后传向输出层，当输出层得到不希望的输出时，则反向传播，将误差信号沿原来的神经通路返回，同时不断修改连接权值和阈值。BP网络的实质是求解误差函数的最小值问题，利用它可以实现多层前馈神经网络权值的调节。BP算法可以使网络权值收敛到一个最终解，但并不能保证所求的误差为全局最优解，也就是容易陷入局部极小值。

1.2 RBF神经网络的基本原理

RBF神经网络（radial basis function neural network）是单隐层前馈型神经网络，输入层节点只是传递输入信号到隐层，它是一个三层前向网络。RBF神经网络的显著特点是隐含节点的基函数采用的是距离函数，并使用RBF作为激活函数。RBF关于n维空间的一个中心点具有对称性，神经元输入距离该中心越远，激活成功率就越低，这个局部特性可以看出RBF神经网络不同与BP神经网络，它是一个局部响应网络，所以训练速度更快，同时缺点也是当样本输入区域较大时，如何保证足够的输入区域，是能否保持学习精度的研究重点，另外与BP神经网络不同的是，它不需要误差的反向传播，节省了大量的运算时间，而且需要确定的参数较少，仅需确定散布常数（SPREAD）。散布常数的确定方法一般采用凑试法和聚类法，本文采用的是凑试法。

2 挖掘机动臂的有限元试验

2.1 挖掘机动臂简介

液压挖掘机随着国家基础建设工作的普及，得到快速的发展。工作装置是液压挖掘机的重要部件，对挖掘机性能有着十分重要的影响。挖掘机动臂的整体式弯臂采用大圆弧过渡以减小该地方的应力集中。主体框架由上盖板、下盖板、左侧板、和右侧板焊接而成。上下盖板，左右侧板均由前后厚度为5～19 mm的16 Mn钢板拼焊而成。动臂与转台、斗杆、动臂油缸连接的轴座均由ZG270-500材料焊接而成，轴座四周焊有四块加强筋板以提高强度。

2.2 挖掘机动臂优化变量选取及有限元模型

［7-8］介绍了动臂参数的优化，主要集中在动臂外形几何尺寸的优化，对动臂焊接板厚度的研究却很少。本文选取的变量为上盖板厚度d0、下盖板厚度d1、左右侧板厚度d2、上耳板厚度d3、前耳板厚度d4。首先在ABAQUS中应用壳体建模，建立了包括上盖板、下盖板、左右侧板、前后耳板等零件，在软件中完成装配，方便针对不同厚度的薄板进行赋予属性。有限元模型如图1。

图1 挖掘机动臂有限元模型

2.3 计算工况选取以及边界条件处理

a）计算工况

本文计算工况选取为挖掘机动臂可能出现的最大载荷工况来计算，即动臂缸全缩，斗杆与斗杆缸铰接点、斗杆和铲斗铰接点及铲斗齿尖在同一直线上且垂直于斗杆缸。

b）有限元模型约束和载荷的处理

为了消除模型的刚体位移，对动臂和转台的铰点，约束其x，y，z方向的移动自由度与绕x，y轴的旋转自由度，释放z方向的旋转约束（ROTZ）。对动臂与斗杆的铰点，约束其y方向的移动自由度，对其他与油缸的铰点以施加载荷的方式处理。

c）各铰点销孔处理方法

由于动臂是通过销轴孔处通过接触传力，销轴孔力不是按照均匀分布而是近似的余弦分布，且存在一定的接触应力集中现象。为了减少计算误差，同时又不致使运算计算量加大，本文在ABAQUS软件中销轴孔中心设置reference points（RP），利用RP与销孔表面设置结构耦合约束，通过RP来施加载荷模拟接触受力（图2）。

图2 销孔的受力处理

2.4 正交设计试验安排

正交试验设计是利用数理统计学和正交性原理，从大量的试验点中挑选适量的具有代表性的试验点，应用正交表合理安排多因素试验的一种科学的试验设计方法。其主要的优点是利用较少次数的试验，得到因素对目标函数影响显著性及其影响规律。根据挖掘机动臂参数特点，选取五因素四水平的正交表L16（4）5，其中16为试验次数，4为因素的水平数，5为因素数。具体试验安排及试验结果如表1，最终动臂应力云图（图3）。

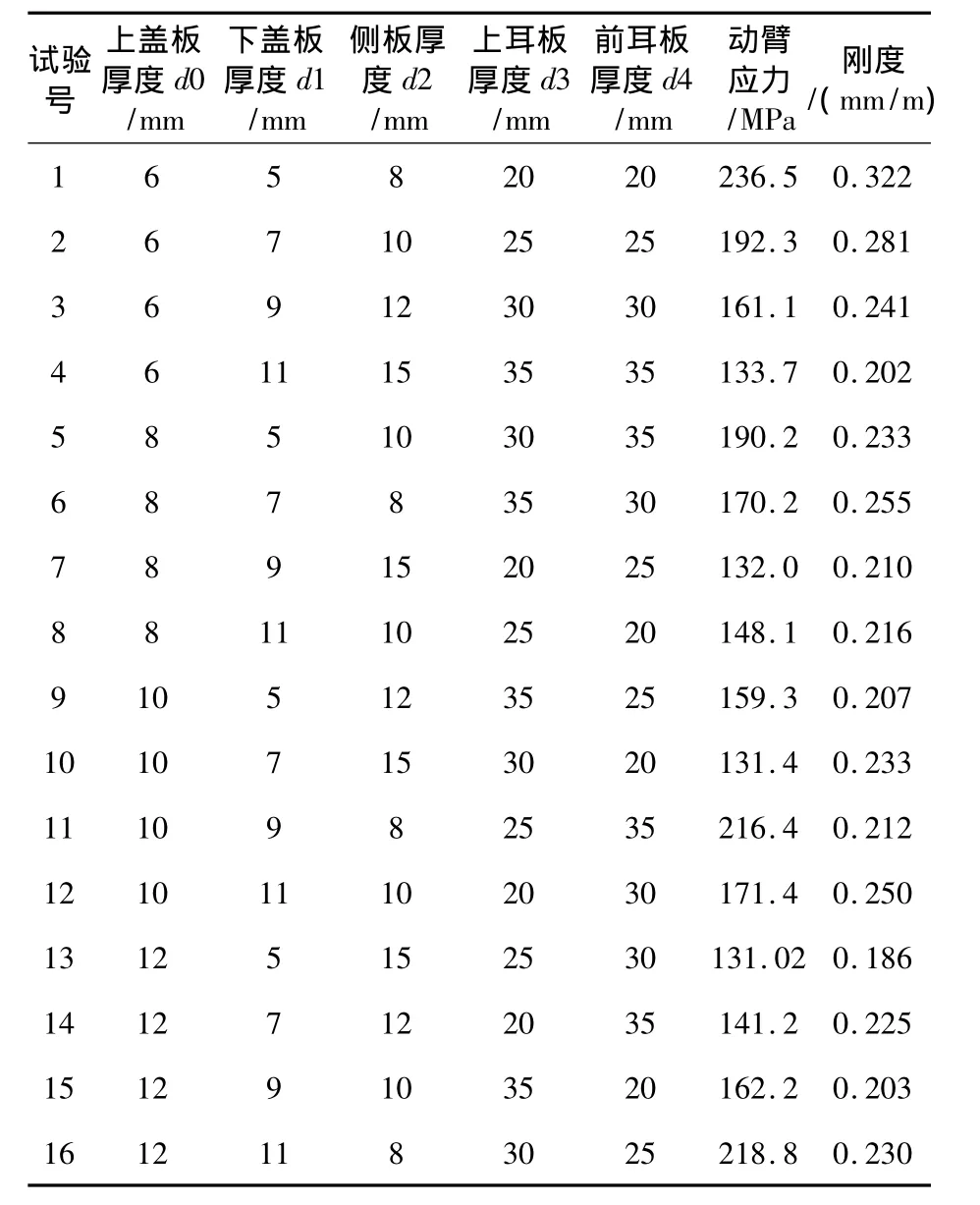
表1 正交试验结果

图3 挖掘机动臂应力云图

3 神经网络的设计与仿真

3.1 数据归一化处理

由于网络输入节点物理量各不相同，有的数值差距非常大，各指标样本之间不存在可比性，无法进行正确的综合评估。且大多数神经网络模型采取S形的函数做为激活函数，该函数的值域在【0，1】区间内。因此需要对数据进行归一化处理，本文采用激活函数的极大值和极小值分别为1和0，所以本文将数据归一到区间【0.05，0.95】内，以便让样本有足够的增长空间，采用的归一化公式为:

式中:Xmax，Xmin是样本变量的最大值和最小值;Xi和Xi'分别是归一化前和归一化后的值。

3.2 BP神经网络与RBF神经网络设计

所有网络设计都在MATLAB软件中创建，BP神经网络采用三层的网络设计，隐含层传递函数选择tansig，训练方法选择 trainlm，调用语句 net=newff（P，T，7，{‘tansig’}，’trainlm’）完成BP网络的创建;RBF神经网络不需要进行各种参数确定，只需要确定散布常数SPREAD，采用凑试法，从 0.5，0.7，0.9，1.1……2.0 中逐一试验，确定最佳的 SPREAD 值为0.7，调用 net=newrbe（P，T，0.7）完成径向基网络创建。两种网络训练误差曲线如图4，图5。

3.3 BP-RBF组合神经的网络设计

BP神经网络采取BP算法反向传播，容易陷入局部最小值，泛化能力较差，利用BP神经网络与RBF神经网络串联，通过RBF的快速逼近，对BP网络进行进一步训练。其中第一部分为BP神经网络，第二部分为RBF神经网络，两种神经网络中的神经元层与层间没有连接，层间全连接。网络结构模型如图6。

图6 BP-RBF组合神经网络模型

在BP-RBF组合神经网络中，BP神经网络的设计和3.2条中相同，输入层为个数为16，隐含层为7，传递函数为S型函数，输出层为2;RBF神经网络比3.2条中精简，其输入层个数与BP神经网络输出层相同，散布常数SPREAD值需要重新试验确定，传递函数使用高斯函数，仿真编程在MATLAB中部分代码如下:

3.4 三种神经网络预测结果分析对比

分别将组合神经网络，BP神经网络，RBF神经网络的预测结果进行对比，检测样本的预测误差对比如表2，表中样本数据为归一化后的数据。

表2 三种神经网络预测误差的对比

3 0.08 0.11 0.14 0.8 0.8 213.7 210.3 0.014 2 184.8 0.131 9 210.5 0.014 9 4 0.14 0.17 0.26 0.8 0.5 153.5 135.5 0.117 2 151.0 0.016 2 151.0 0.016 2 5 0.20 0.11 0.14 0.8 0.5 205.7 192.9 0.047 6 186.1 0.123 4 195.5 0.048 7 6 0.14 0.05 0.35 0.5 0.95 144.1 131.7 0.089 4 141.5 0.018 1 141.5 0.018 1

由仿真分析对三种神经网络做一下对比:

从网络结构上，BP神经网络和组合神经网络的网络结构较RBF神经网络精简，其中BP神经网络隐含神经元为7，组合神经网络的第一隐含层神经元数为7，0神经网络的隐含层神经数为16。在BP神经网络中，sigmoid神经元能覆盖较大的输入区域，而径向基采用高斯函数作为传递函数决定了其只能对较小的区域产生响应，径向基的隐藏神经元等同于学习样本数，所以当输入区间较大，学习样本较多的时候RBF神经网络需要更多的神经元去满足预测精度，导致了网络结构的冗赘。

从预测精度上，三种神经网络都展现了良好的训练精度，证明神经网络预测应力的方法是可行的。其中BP神经网络在3、4号预测样本中的误差出现了较大的跳跃，误差大于百分之10;RBF神经网络预测平稳，仅在6号样本出现百分之8的误差;BP-RBF组合神经网络中通过RBF网络的进一步训练，两处跳跃误差得到了改善，在预测精度上组合网络显示出优于BP和RBF神经网络的性能。

训练时间上，BP神经网络的训练时间为32.7 s，迭代200次;由于RBF神经网络避免了BP网络冗赘的反向误差传播计算，通过局部映射大大提高了训练速度，RBF神经网络训练代数仅为20次，训练时间为7.2 s;RBP神经网络了较快的收敛速度，大于BP神经网络和组合神经网络

综上可知，RBF神经网络和组合神经网络可实现互补应用，当学习样本较少的时候采用RBF神经网络实现较快的收敛，较平稳的预测精度;当学习样本众多，输入区间跨度大的时候，为了精简网络结构，防止误差跳跃，可以利用BP-RBF组合神经网络实现精简的网络结构和满意的预测精度。

4 结语

本文分析了BP神经网络和RBF神经网络在应力预测中的应用特点，提出了BP-RBF组合神经网络，通过实例仿真证明了，BP-RBF组合神经网络的误差满足工程应用需求，并提高了BP神经网络在应力应变预测中的准确度，解决了RBF神经网络学习样本繁多时候，需要相应多的神经元的问题，具有普适性。可以和RBF神经网络结合使用解决各种输入样本情况下的结构优化问题，提高运算效率。

参考文献:

［1］李艳聪，张连洪.基于神经网络和遗传算法的液压机上梁轻量化和刚度优化设计［J］.机械科学与技术，2010，（2）:164-169.

［2］朱学军，薛量，王安麟，等.利用神经网络实现复杂结构的多目标优化设计［J］.机械科学与技术，2000，（3）:368-370.

［3］田雨波.混合神经网络技术［M］.北京:科学出版社，2009.

［4］麻官亮，邵玉刚.BP和RBF神经网络在边坡稳定性评估中的比较研究［J］.路基工程，2012，（1）:161-164.

［5］孙大洪，王发展，刘强，等.基于BP和RBF神经网络的滚动轴承故障诊断比较［J］.轴承，2010，（2）:53-56.

［6］孙德丰.MATLAB神经网络仿真与应用［M］.北京:电子工业出版社，2009.

［7］朱奇，孙纪燕.液压挖掘机动臂优化设计［J］.工程机械，2008，（9）:34-36.

［8］黄美美，赵婷婷.液压挖掘机动臂有限元分析［J］.设计与研究，2006 ，（8）:19-22.

［9］牟洪波，戚大伟.基于BP和RBF神经网络的木材缺陷检验研究［M］.哈尔滨:哈尔滨工程大学出版社，2011.