基于对称角度分割法使用正弦规测量大角度的新方法

吕舒波，黄皖卿，汤武，孙长敬

（中国计量学院质量与安全工程学院，浙江杭州 310018）

0 引言

随着科技的发展，角度测量对测量器具的精度要求越来越高。正弦规是测量角度比较方便的器具，测量0°～30°的零件角度尤为精确，但是当测量＞30°的角度时，其精确度明显下降。为了能够充分发挥正弦规的作用以及提高其精确度，本文提出“对称分割法”，对＞30°的角度进行测量和分析，并与传统测量方法的精确度进行比对。

1 正弦规测量角度分析

正弦规，又称正弦尺，是采用间接法测量角度的常用量具之一。其测量原理如图1所示:先根据式（1）以被测角度的公称尺寸α求得尺寸H，并用量块组合成H尺寸，再利用测微仪进行测量，最后根据测微仪在被测角度两端的示值之差，即可求得被测角度与其公称角度值的偏差Δα（即被测角度的误差值）［1］。

式中:α——被测角度公称值;

L——正弦规两圆柱轴心距;

H——根据被测角度公称值算出的尺寸。

由式1可得:

对式2两边全微分，得:

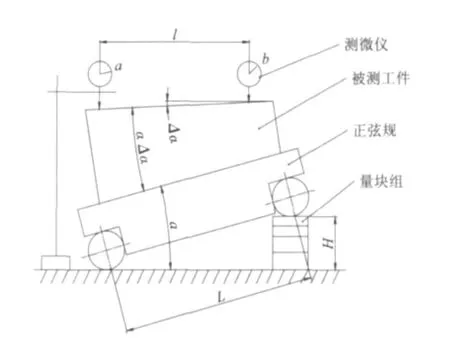
图1 测量原理图

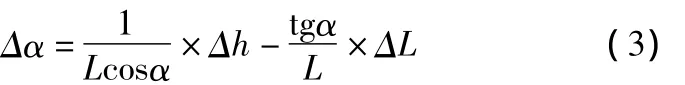
式中:Δα——被测角度与其公称值的偏差;

Δh——量块组组合尺寸与实际计算尺寸H的偏差;

ΔL——正弦规两圆柱轴心距偏差。

由式3可知，被测角度与其公称值的偏差Δα不仅与Δh和ΔL有关，还与正弦规中心距L和被测角度α有关。L越大，Δα越小;Δα随被测角度α增大而增大。当被测角度＜30°时，变化不显著，＞30°（特别是 ＞45°时），误差 Δα 的增加则较明显。所以，传统的正弦规测量角度的方法一般只适用于测量角度 ＜30°的零件［1］，测量精度可达到3'～5'［2，5，13］。

2 正弦规测量大角度的新方法

如上所述，正弦规不适应测量＞45°的角度限制了其在实际测量中的应用。受正弦规测量小角度原理的启发，本文提出了一种利用正弦规测量大角度的新方法。新方法的主要思路是:将被测角度分割成若干小角度分别进行测量，再对测得值进行处理即可得到被测角度值。该方法的难点在于如何分割被测角度。为简化后续分析，本文采用“对称角度分割法”，即利用被测角度的角平分线进行分割。其测量原理如图2所示。

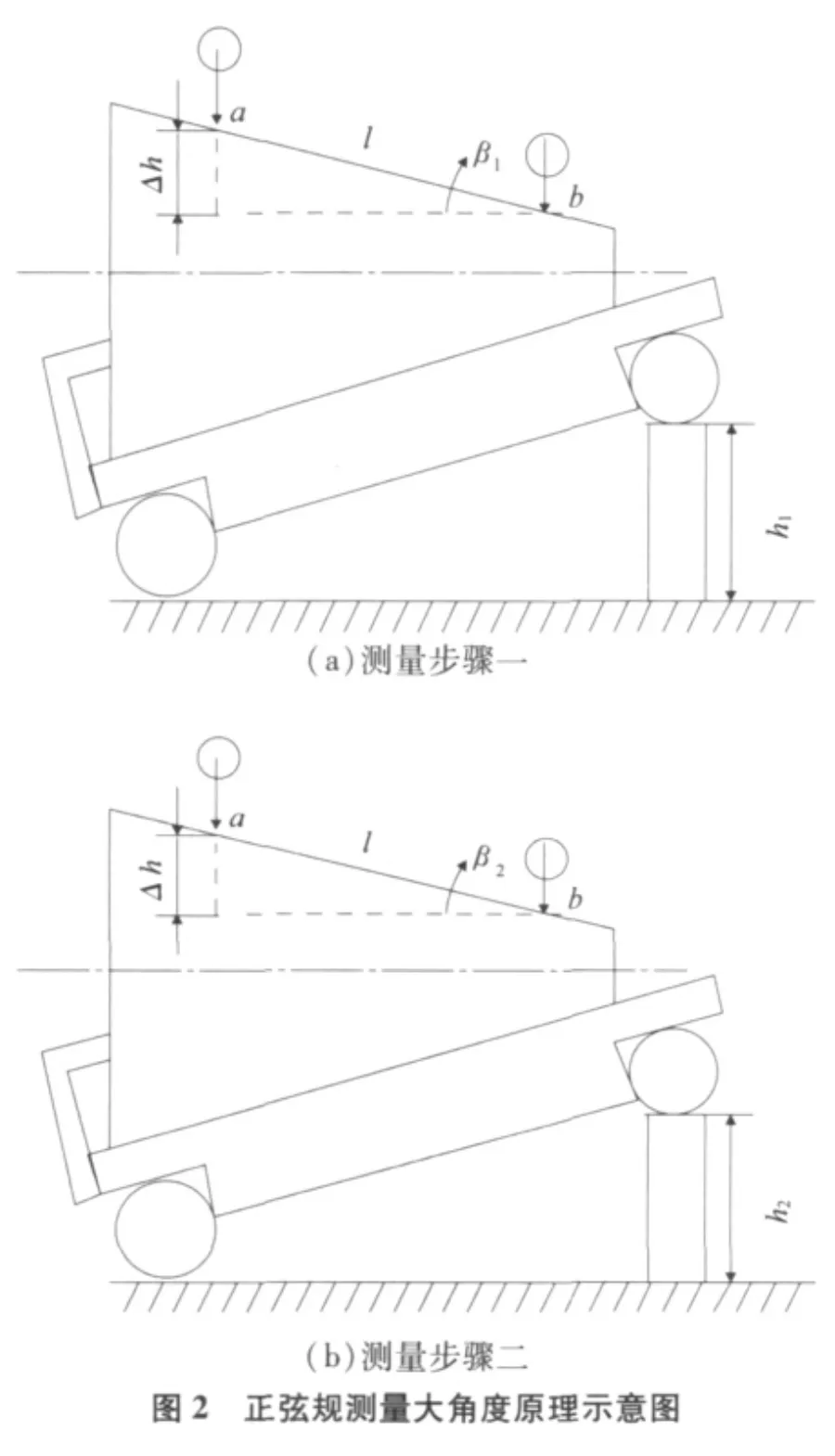
由图2（a）可得:

先由式（4）计算并用量块组合出尺寸h1，再用测微仪测出被测角度上面距离l的a，b两点的高度差Δh，再由式（5）求得 β1:

将被测角度翻转180°（即被测角度的另一面朝上），根据式（6）求得h2:

再用量块组合出尺寸h2，按上述同样方法求出β2，则被测角度β的测量值为［10-13］:

3 实际测量验证

为验证正弦规测量大角度新方法的有效性及其与传统方法的比较，本文在相同的实验室环境下，选择公称值位于35°～80°之间的10个不同角度的角度块，利用传统方法和新方法分别进行了实际对比测量。每个被测角度快各测量三次，取平均值作为该被测对象的测量结果，分别记于表1和表2中。图3所示的是实际测量值与公称值的一致性比较。新老方法测量相对误差如图4所示。其中，相对误差的定义是:

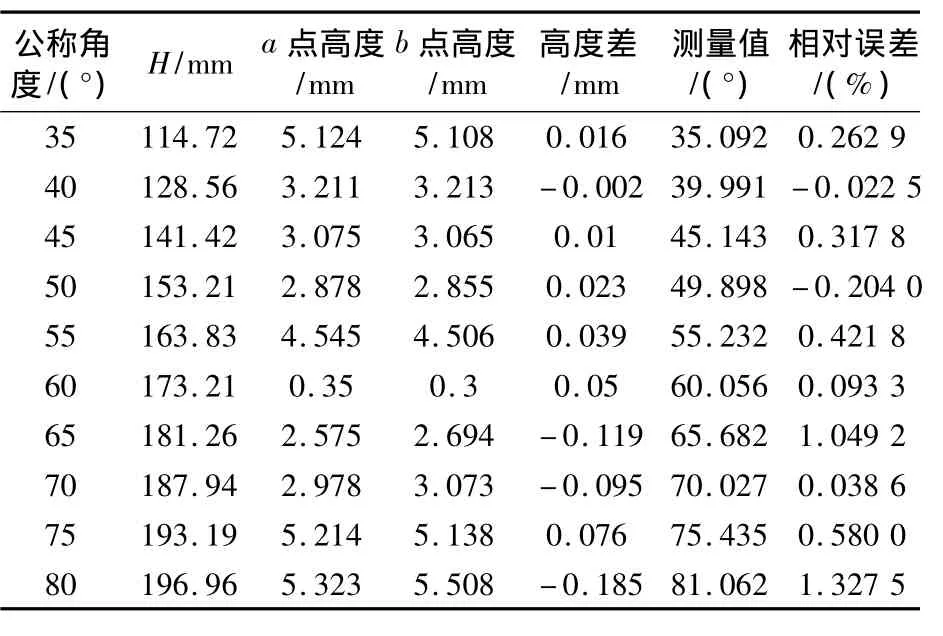
表1 传统方法测量数据

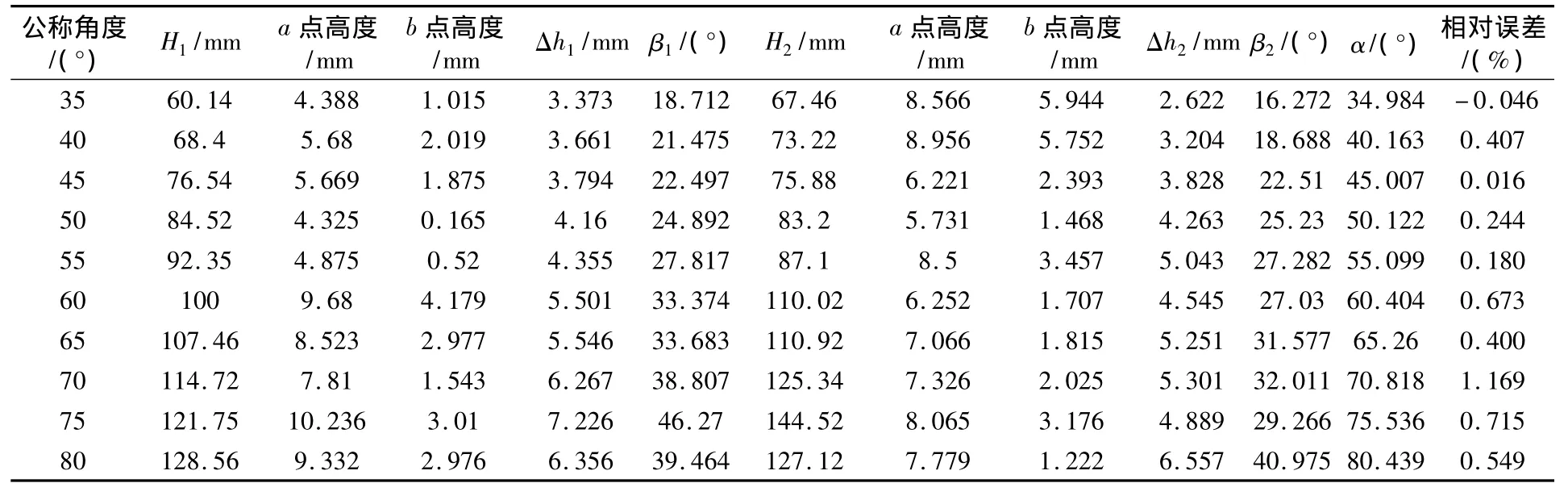
表2 新方法测量数据

图3 新老方法测量数据比较

由图3可知，针对35°～50°之间的被测角度，新方法和传统方法的测量值与公称值曲线的吻合都较好;测量＞50°的角度时，新老方法的测量值与公称值曲线均有所偏离，且偏离的幅度也基本一致。因此可得出结论:测量＜50°的角度时，新老方法均具有较高的且基本一致的测量精度;对于＞55°的角度，两种方法的测量误差均有所增加。从图4所示的相对误差曲线上也可以看出，被测角度＜55°时，新老方法的相对误差基本一致，测量＞55°的角度时，新方法曲线波动的幅度比老方法有所减小。

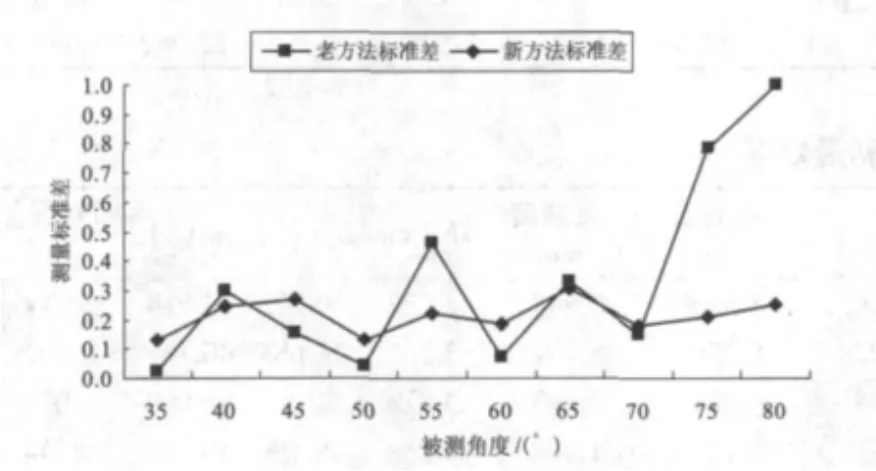
图4 相对误差曲线图

为进一步验证新老测量方法在测量稳定性方面的差异，针对某一角度进行多次测量，用数据的标准差来进行比较。由于新方法主要针对大角度的测量，所以选择5个角度（60°、65°、70°、75°、80°）分别进行三次的测量，测量结果及其标准差如表3所示。新老测量方法的标准差曲线如图5所示。

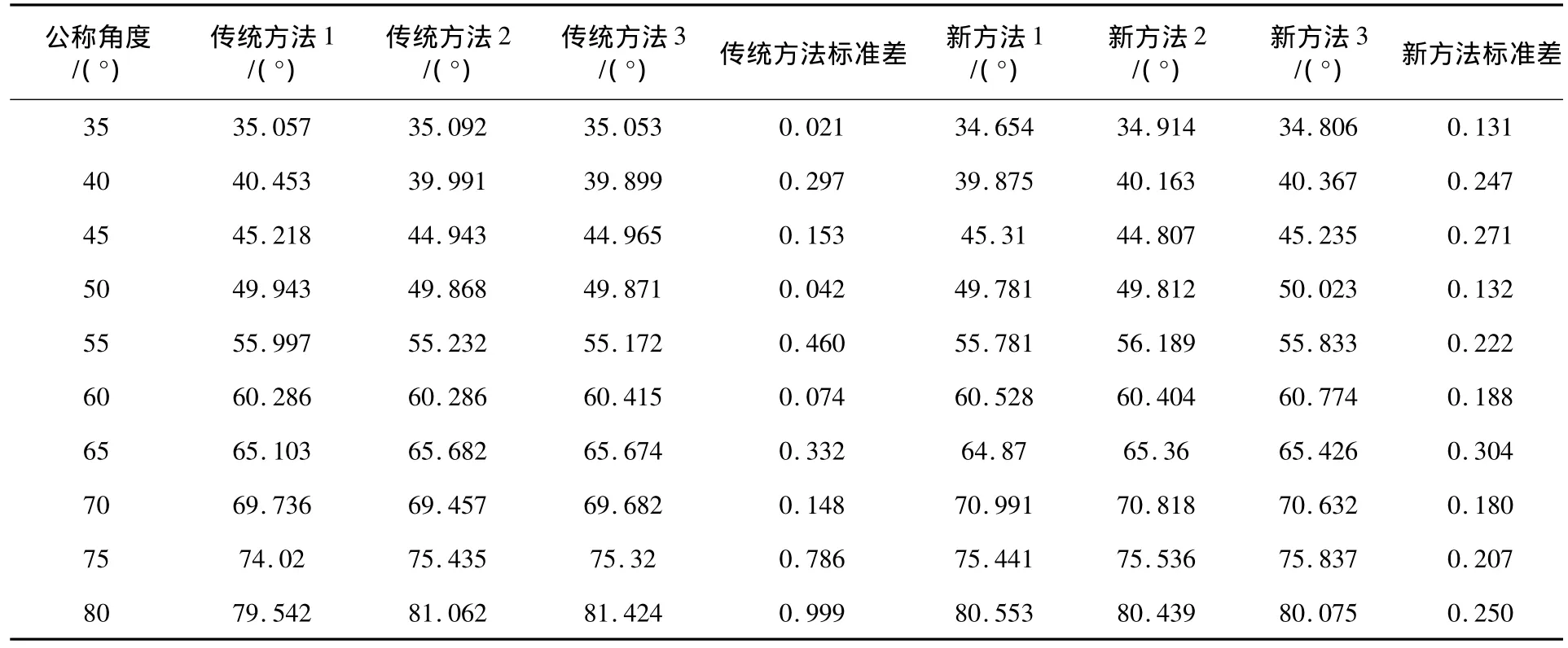
表3 多次测量后的标准差

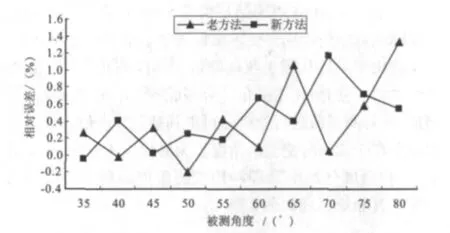
图5 标准差曲线图

从图5所示的新老测量方法标准差曲线对比图上可以看出:新方法标准差的波动较小，而传统方法在被测角度较小时也较平稳，但测量较大角度时，其标准差的波动明显变大。这在一定程度上可以说明新方法比传统方法更适合测量大角度。

4 结论

本文针对利用正弦规测量角度传统方法存在的不适应于测量大角度的不足，创新思路，提出了一种基于平分角度、分次测量的方法，实现了利用正弦规测量大角度的可能，并通过新方法和传统方法的对比测量，验证了新方法测量大角度的可行性、测量精度的有效性及稳定性。数据分析结果显示，新方法在测量小角度时与传统方法基本没有区别，测量大角度时，新方法解决了传统方法不足，但该方法只适用于对称角度，且被测角度＞45°后，其测量误差较大。换言之，当对测量精度要求不高时，可以利用新方法进行大角度的测量。本文提出的新方法对大角度的测量有一定的指导意义。

［1］王红敏，石沛林，郑国强.正弦规应用及误差分析［J］.山东工程学院学报，2002，16（4）:61-64.

［2］张雪粉，张育增.用正弦规测量圆锥角实验的误差分析［J］.沈阳航空工业学院学报，2002，19（2）:36-37.

［3］刘兴富.用正弦规测量内锥角的方法［J］.机械制造，2002，40（10）:458.

［4］韩喜春，吴东艳，张鹏.AS5040在角度测量中的应用［J］.传感器与微系统，2006，25（6）:75-77.

［5］刘兴富.内外圆锥角的精确简便测量方法［J］.机械工业标准化与质量，2007，（1）:45-47.

［6］Qinggang Liu，Yiping Li，Wenyong Zhao，et al.Two Dimensions Angular Sensor for Micro/Nano Measurement［J］.IEEE，2007:274-277.

［7］杨国强.正弦规测量角度及锥度的探索［J］.林区教学，2007，（3）:25-26.

［8］ Massimiliano Donno，Elia Palange，Fabio Di Nicola.A New Flexible Optical Fiber Goniometer for Dynamic Angular Measurements:Application to Human Joint Movement Monitoring［J］.IEEE，2008，57（8）:1614-1620.

［9］贾晓杰.正弦规两圆柱磨损对综合误差的影响［J］.中国计量，2008，（7）:93.

［10］方力.正弦规的另一种使用方法［J］.机械制造，2009，47（533）:63-65.

［11］刘兴荣，张小希，马桂茹，等.一种新型实用的内锥锥角测量方法［J］.中国计量，2009，（5）:87-89.

［12］柴学宝.正弦规测量燕尾配合件角度的原理与方法［J］.天津职业院校联合学报，2009，11（2）:24-26.

［13］刘兴富.正弦规上测量内外圆锥体的精确简便方法［J］.装备制造技术，2005，（1）:27-29.

［14］王晓英，姜静，李正.提前器总成角度测量装置的设计与研究［J］.现代车用动力，2010，（4）:55-57.

［15］周万民.角度投影的大小分析［J］.燕山大学学报，2002，26（2）:124-127.