极限与配合相关公式简单记忆方法

阚萍

（四川信息职业技术学院，四川广元 628017）

技术测量中极限与配合的内容涉及到术语多、公式多、关系多、符号多，并且这些内容需要掌握应用。在教学过程中，极限与配合出现的大量公式让学生在课堂上很难记住，应用起来也会感到无从下手，这样会影响到学生学习的积极性，甚至会直接影响到教学质量。在教学过程中，如果能把这些内容化难为易，把枯燥的公式变成形象的记忆就显得十分重要。现将结合本人的教学实践，对光滑圆柱体结合的极限与配合所涉及到的公式的记忆方法，做简单的说明。

1 理解基本术语及定义并记忆符号

光滑圆柱体结合的极限与配合所包含的基本术语及定义有尺寸、偏差、公差及配合。在内容上的安排应该做到由浅到深，层层深入，这样对学习和理解都有很大的帮助。在理解孔与轴的定义之后，就会讲到基本术语及定义，同时还有相对应的符号。孔的符号用大写字母表示，轴的符号用小写字母表示。

在有关尺寸的基本术语及定义中，基本尺寸、实际尺寸与极限尺寸有相对的符号表示。基本尺寸是由设计给定的尺寸;实际尺寸是通过测量获得的尺寸，并非是被测尺寸的真值;极限尺寸是孔、轴允许的尺寸的两个极端。对这些公式与符号记忆并没有困难。

偏差的定义是某一尺寸与基本尺寸的代数差。这里提到代数差说明结果可能是正值、负值或零，那么除零外要标注“+”号或“-”号。极限偏差是上偏差和下偏差的统称。极限偏差是用极限尺寸减其基本尺寸所得的代数差。上偏差（孔用ES表示，轴用es表示）为最大极限尺寸减其基本尺寸所得的代数差;下偏差（孔用有EI表示，轴用ei表示）为最小极限尺寸减其基本尺寸所得的代数差。

公差是指允许尺寸的变动量［1］，所以公差是一个没有符号的绝对值。

配合是指基本尺寸相同的、相互结合的孔和轴公差带之间的关系。相配合的孔和轴公差带之间关系不同，形成的配合就不同。配合种类有三种，即间隙配合、过盈配合及过渡配合，其中求解极限间隙与极限过盈有相应的公式。

2 掌握偏差、尺寸公差与配合公差的公式关系

光滑圆柱体极限与配合术语多，所对应的量之间存在着一定的联系和计算公式，理清之间的关系，巧妙的掌握计算公式，应用起来就得心应手。

孔的尺寸公差用符号Th表示，孔的尺寸公差等于孔的上偏差减其下偏差，公式为ES-EI=Th;轴的尺寸公差用符号Ts表示，轴的尺寸公差等于轴的上偏差减其下偏差，公式为es-ei=Ts。极限偏差与公差之间的公式关系可以用简化的口诀来记忆，“上下有正负，相减为公差，公差加两竖。”相配合的孔、轴的公差之和等于配合公差，配合公差符号用Tf表示，公式为Th+Ts=Tf，记忆口诀为“孔轴相加Tf”。汇同前面的口诀就是“上下有正负，相减为公差，公差加两竖，孔轴相加Tf。”做到很好的理解公式之间的关系，对于记忆口诀帮助很大，在解题过程中能够快速的求解出正确答案。那么，首先用图形的方法来演示孔、轴相配合时公式之间的关系，如图1所示。学习过程中加以手势的比划，理解图形之后再记忆口诀，可以快速有效的掌握各量之间的关系。

图1 孔轴相配合偏差与公差关系图

3 掌握极限盈隙的公式关系

根据相互结合的孔、轴公差带之间不同的相对位置关系，配合分为三种:间隙配合、过盈配合以及过渡配合。

由于孔和轴的实际尺寸允许在各自公差带内变动，因此在间隙配合中孔与轴配合的间隙是变动的。当孔为最大极限尺寸轴为最小极限尺寸时，配合最松，之间存在的间隙最大;当孔为最小极限尺寸而轴为最大极限尺寸时，之间存在的间隙最小。其性质用最大间隙Xmax、最小间隙Xmin表示，极限间隙计算公式分别为:

过盈配合中的过盈也是变动的。当孔为最大极限尺寸轴为最小极限尺寸时，之间存在的过盈最小;当孔为最小极限尺寸而轴为最大极限尺寸时，之间存在的过盈最大。其性质用最小过盈Ymin、最大过盈Ymax表示，极限过盈计算公式分别为:

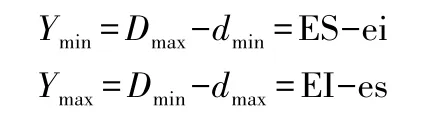
过渡配合关系的孔和轴装配后可能具有间隙，也可能具有过盈。当孔为最大极限尺寸轴为最小极限尺寸时，之间存在的间隙最大;当孔为最小极限尺寸而轴为最大极限尺寸时，之间存在的过盈最大。其性质用最大间隙Xmax、最大过盈Ymax表示，公式分别为:

配合公差是允许间隙或过盈的变动量。在极限盈隙中计算的公式如下:

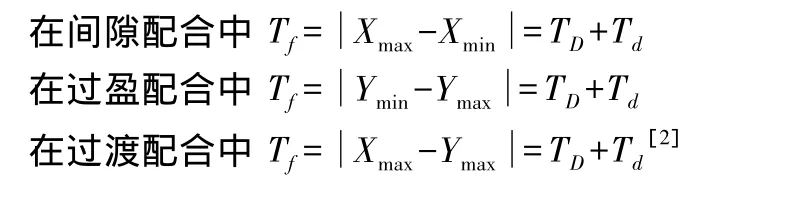
4 图形表示及举例

通过以上极限盈隙关系式可以看出，Xmax与Ymin的计算公式是一样的;Xmin与Ymax的计算公式是一样的。将以上的公式关系继续用图1表示，此处省略文字“孔的基本尺寸”、“轴的基本尺寸”。如图2极限盈隙关系图所示。

图2 极限盈隙关系图

Xmax与Ymin的计算公式是一样的，都是用孔的上偏差减轴的下偏差，简单的说是孔上减轴下，用简单的口诀记忆就是“大间小过上减下”。如图3所示。

图3 大间小过上减下图

Xmin与Ymax的计算公式是一样的，都是用孔的下偏差减轴的上偏差，简单的说是孔下减轴上，这里同样用简单的口诀记忆为“小间大过下减上”。如图4所示。

图4 小间大过下减上图

首先判断此配合为间隙配合，那么就要计算最大间隙与最小间隙。用口诀的方法求此题为:

“大间小过上减下”——Xmax=ES―ei=（+0.021）―（―0.033）=+0.054。

“小间大过下减上”——Xmin=EI―es=0―（― 0.020）=+0.020。

“孔轴相加Tf”——Tf=Th+Ts=0.021+0.013=0.034。

应用图形表示如图5所示。

图5 计算盈隙图解

5 结语

在教学过程中，教师起到启发和引导的作用，学习的主体还是学生，主要还是靠学生独立思考与深入理解。教师应该用有效的教学方法去激起学生的学习积极性。光滑圆柱体极限与配合所涉及到大量的术语与符号，以及计算公式。理清量与量之间的关系，寻找其中的联系，采用理解图形记忆口诀的方法，把重要的枯燥公式变得简单易学，这样学生也能够更好的掌握应用极限与配合的内容。

［1］冯丽萍.《公差配合与测量技术》［M］.第1版.北京:机械工业出版社，2011.

［2］顾元国.《公差配合与测量技术》［M］.第1版.北京:北京理工大学出版社，2008.