基于HyperMesh的车架拓扑优化设计

任启丰，王 军，王 浩

(合肥工业大学 机械与汽车工程学院，安徽 合肥 230009)

车架一般由2根纵梁和几根横梁组成，经悬挂装置﹑前桥﹑后桥支承在车轮上。由于汽车大部分零部件都安装在车架上，车架承受的载荷比较复杂。车架的强度、刚度以及动态特性直接影响整车的使用寿命、乘坐舒适性、操纵稳定性等基本性能。

本文采用UG软件建立车架模型，利用HyperMesh进行网格划分，获得车架的有限元模型［1］，并对有限元模型进行模态分析。对比试验与理论分析结果，对模型进行拓扑优化，得到使用性能更好的车架结构。

1 模态分析

1.1 模型导入与网格划分

将UG建立的三维几何模型导入到HyperMesh，利用几何清理工具，对模型进行修复，产生简化的几何模型，便于网格划分［2］。车架有限元模型采用壳单元，根据实际车架不同部位赋予单元不同的厚度，有3.0，3.2，3.5，4.0，4.5，5.0，5.5，6.0，8.0 mm 几种。使用的钢板材料属性见表 1。

表1 材料性能表

网格划分时，单元由三角形单元和四边形单元组成，三角形单元比例为3.7%，三角形网格的数目占总网格数目的比例低于10%。车架有限元模型中四边形壳单元有81 690个，三角形壳单元有3 137个。车架有限元模型如图1所示。

1.2 模态分析

对车架进行模态分析，利用静态分析模型［3］，获取车架的自由模态。设置频率范围从1 Hz开始，得到的模态频率如表2所示。采用多点激振，进行车架自由模态试验，见图2，模态试验数据如表3所示。

将数值计算模态与试验测试模态进行对比分析见表4，以验证有限元模型的准确性。表4中的相对误差f=(f2－f1)/f2×100%。

对比可知，数值模态和试验模态的前8阶固有频率最大误差均在5%以内，说明所建立的车架有限元模型可信度较高，可以用于进一步的研究。

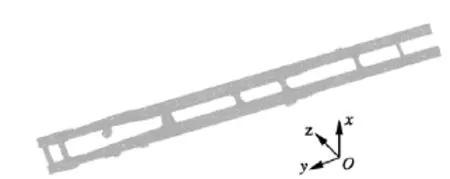
图1 车架有限元模型

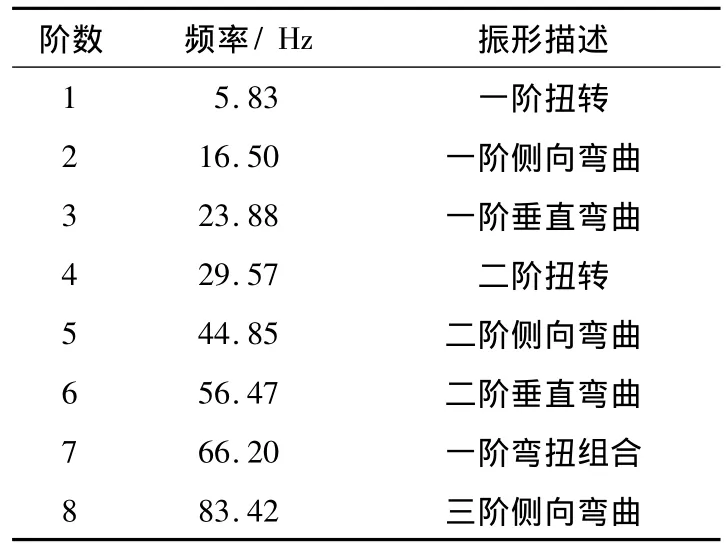
表2 车架模态频率及振型

图2 车架模态试验

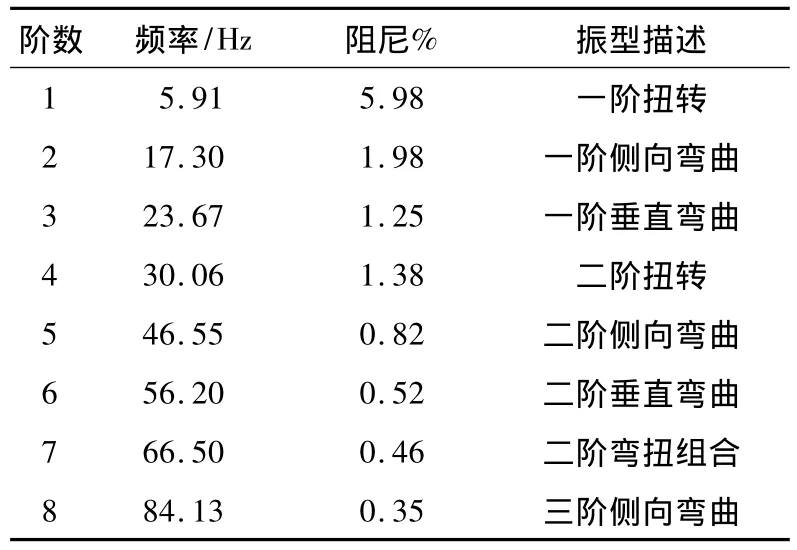
表3 车架模态试验数据与振型

表4 计算模态与试验模态对比

载货汽车在行驶过程中，激励源主要是路面激励和发动机激励。其中路面激励频率多在3 Hz以下。根据发动机激励频率的计算公式，得到怠速及额定转速时发动机的激励频率分别为35，115 Hz。

从整车振动的角度考虑，车架低阶主要振型的频率(一阶弯曲和一阶扭转)应控制在3～35 Hz。由以上计算结果可见，该车架前几阶固有频率刚好在要求的频率范围内，能够在较大程度上避免共振现象的发生。

2 拓扑优化

2.1 拓扑优化算法

变密度算法［4］将结构内所有材料的单元密度都视为相同，对单元密度进行优化计算，从而获得结构的最优材料布局。数学模型为

式中 ηi为i单元密度;Fi为体积力;ti为i单元的面积力;ui为位移向量;Vi为体积变量;m0为材料质量的上限;m*为优化时去掉的材料质量;Δ为优化时除去的质量与原质量的比例;ε为密度下限;J1，J2，…，Jk为优化后单元密度没有变化的单元号;n为单元个数。

2.2 定义目标函数和约束

在本文的研究中，需求解出车架的结构布局。因此，定义选定的拓扑区域材料分布为优化变量;弯曲工况、扭转工况的柔度指数为最小目标函数;车架结构体积分数为约束函数［5］。

为了获得新车架的拓扑架构，建立与原车架尺寸对等的拓扑结构模型，如图3所示。在此模型上添加载荷和约束，对车架进行各种工况下的受力运算。根据运算中材料的分布形式，结合原有车架结构，合理布局新车架材料。

图3 拓扑优化模型

2.3 优化结果

优化时，将体积比设置为0.3，即消减材料70%以上，对车架进行拓扑分析，图4，5为拓扑优化结果，优化结果是以单元密度分布形式显示的，表现为材料设计最优布局的等值面图，图中只显示密度接近1.0的保留部分。图4，5中的数字代表单元的密度，是相对值。

图4 扭转工况单元密度分布图

图5 弯曲工况单元密度分布图

通过对拓扑模拟的分析可得:

1)纵梁区域是人为设定的非拓扑区域，且纵梁是主要的抗弯构件，因此保留原车架的纵梁部分;

2)从拓扑结果云图来看，2个工况下车架后部都保留较多的材料;

3)在扭转工况下，发动机支撑处材料几乎全部保留，故该处的横梁应该保留;

4)在弯曲和扭转工况下，车架中部相近的2个位置分别优化出2根横梁，故原车架此处的2根横梁也要保留;

5)在弯曲工况下，车架前端优化为1根横梁，可以考虑把原车架的2根横梁减为1根。

由以上分析结果看，车架前部保留材料较多，原车架虽然在该处有2根横梁，但是在发动机的支撑处并无横梁，因此把车架前端的第2根横梁后移到发动机支撑处，同时将第1根横梁的厚度由4 mm加大至5 mm。新的车架构造如图6所示。

对修改后的车架进行模态分析，得到车架各阶模态数据如表5所示。

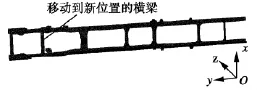
图6 优化后的车架几何模型

表5 优化后车架的模态频率

分析上述拓扑优化后车架的特性参数，将这些参数与原有的车架特性参数比较如表6所示。

表6 优化前后车架性能参数对比

从表6可以看出，拓扑优化后，在没有增加车架质量的前提下，除了车架弯曲刚度几乎没有变化之外，车架其它特性参数指标均有不同程度的提高。其中，优化后车架扭转刚度提高11.5%，说明优化后车架在保持原车架较好的抗弯性的同时，抗扭性也得到改善;车架的低阶固有频率增大，一阶扭转频率增大36.7%、一阶弯曲频率提升11.7%，说明车架的整体刚度有很大的提高。在此前提下，在保证静动态特性的同时，可以通过尺寸优化等优化方法对拓扑优化后的车架进行进一步优化，对车架进行减重分析。

通过与原车对比可以看出，优化后车架的特性参数有大幅度提升，且没有超出车架的设计要求范围。

3 结语

1)模态分析获得车架前8阶模态频率，确定了以选定区域材料分布为设计变量、弯曲和扭转柔度指数为设计目标的优化策略。

2)优化后的车架结构扭转刚度提高11.5%、一阶扭转频率增大36.7%、一阶弯曲频率提升11.7%，总体质量基本保持不变。拓扑优化能够有效改进车架结构、提升车架性能、缩短研发时间、降低设计成本。

［1］李开泰，黄艾香，黄庆怀.有限元方法及其应用［M］.西安:西安交通大学出版社，1992:1－3.

［2］于亚婷，杜平安，王振伟.有限元法的应用现状研究［J］.机械设计，2005，22(3):6 －8.

［3］杨英，赵广耀，孟凡亮.某轿车白车身模态分析和试验研究［J］.东北大学学报:自然科学版，2008，29(7):1045－1048.

［4］石琴，洪洋，张雷，等.拓扑及参数优化方法在专用汽车车架结构设计中的应用［J］.机械设计，2005，22(12):30－33.

［5］杜海珍，荣见华.汽车车架结构的拓扑优化设计［J］.机械设计与研究，2007，23(1):116－119.